Ціль:
Визначення напружено-деформованого стану циліндра з вільними торцями під внутрішнім тиском.
Література:
Warren C. Young, Richard G. Budynas. Roark’s Formulas for Stress and Strain. Seventh Edition. New York, McGraw-Hill, 2002.
Формулювання задачі:
Визначити напруження в стінці циліндра у меридіальному σ1 та окружному σ2 напрямках, а також меридіальні Δу і радіальні переміщення ΔR.
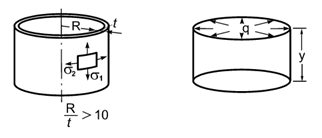
Опис розрахункової схеми:
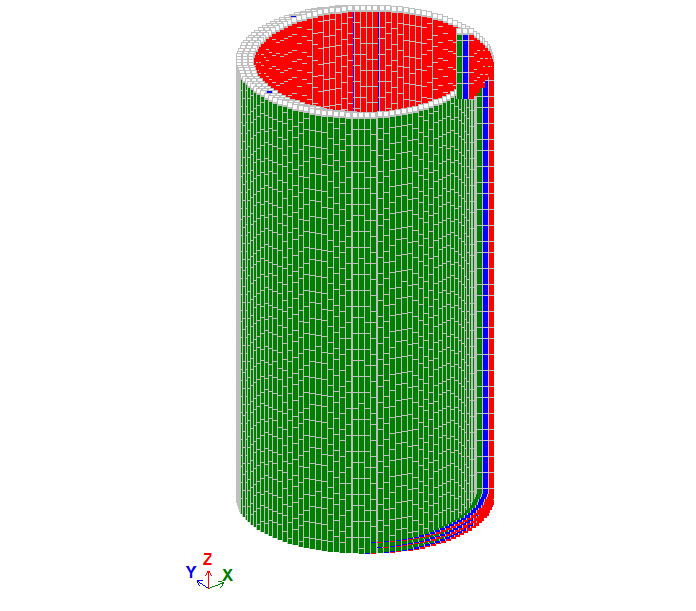
Циліндр вільний від закріплень під впливом внутрішнього рівномірного тиску q.
|
Варіант 1 |
Варіант 2 |
Геометрія:
Радіус циліндра R = 1 м;
Товщина стінки циліндра t = 0,02 м;
Висота циліндра L = 4 м.
Характеристика матеріалу:
Модуль пружності Е = 2,1 * 1011 Па;
Коефіцієнт Пуассона ν = 0,3.
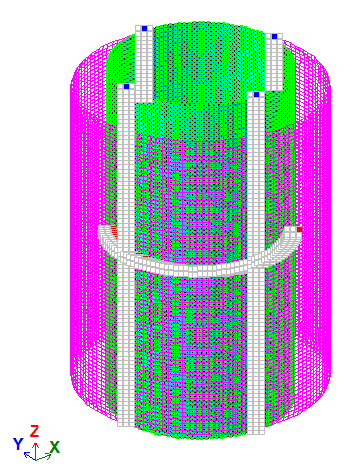
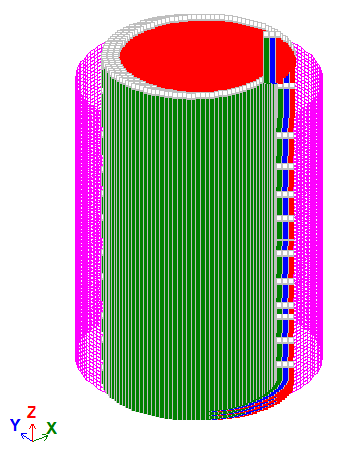
Граничні умови:
В’язі симетрії.
Навантаження:
Внутрішній тиск p = 10000 Па
Примітка:
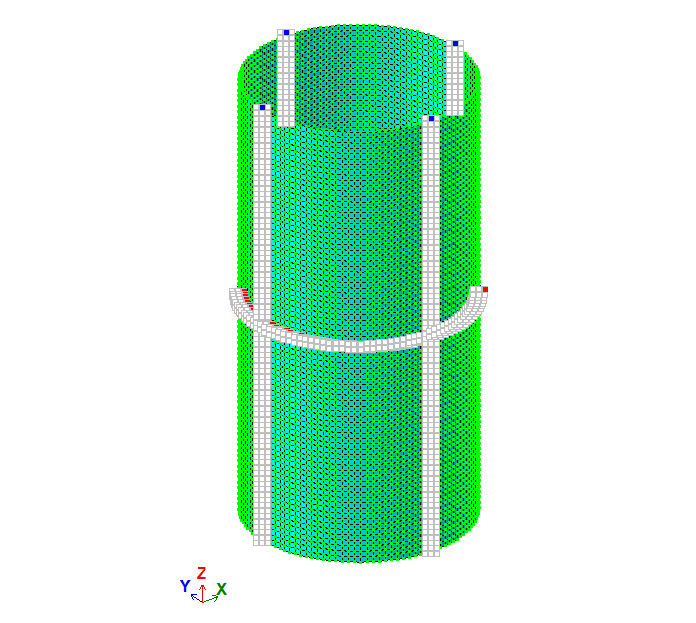
Задача розв’язується у просторовій постановці (ознака схеми 5).
Для побудови схеми використані СЕ 44 – універсальний чотирикутний СЕ оболонки.
При розв'язанні задачі було розглянуто два варіанти:
мембранна теорія оболонок (варіант 1) та загальна теорія оболонок (варіант 2).
Робота циліндричної оболонки відповідно до мембранної теорії досягається шляхом накладання в'язей на всі кутові переміщення у всіх вузлах розрахункової схеми.
Вузлам схеми призначена місцева система координат (місцеві осі вузлів Х1 напрямлені від центра циліндра).
Сітка скінченних елементів має 80 елементів по висоті циліндра і 120 елементів вздовж окружності.
Розмір скінченних елементів: 0,05 х 0,0525 м.
Кількість вузлів: 9720. Кількість елементів: 9600.
Результати розрахунку:
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
Аналітичне рішення:
σ1 = p/t
σ2 = 0
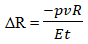
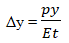
Порівняння результатів розрахунку:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % | ||
| Варіант 1 | Варіант 2 | Варіант 1 | Варіант 2 | |||
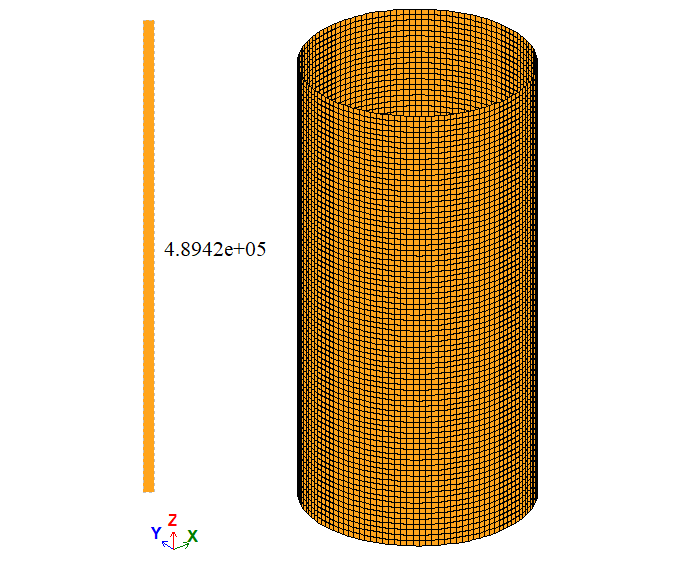
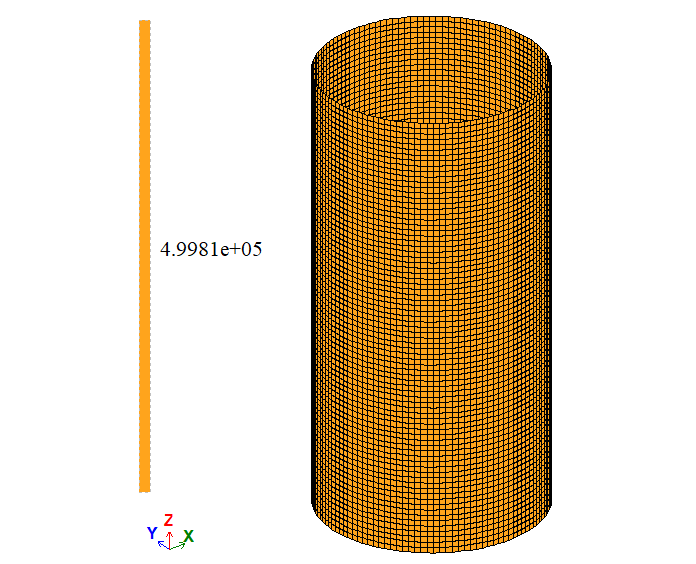
| Точка на поверхні | σ1, Па | 5 * 105 | 4,8942*105 | 4,9981*105 | 2,116 | 0,038 |
| σ2, Па | 0 |
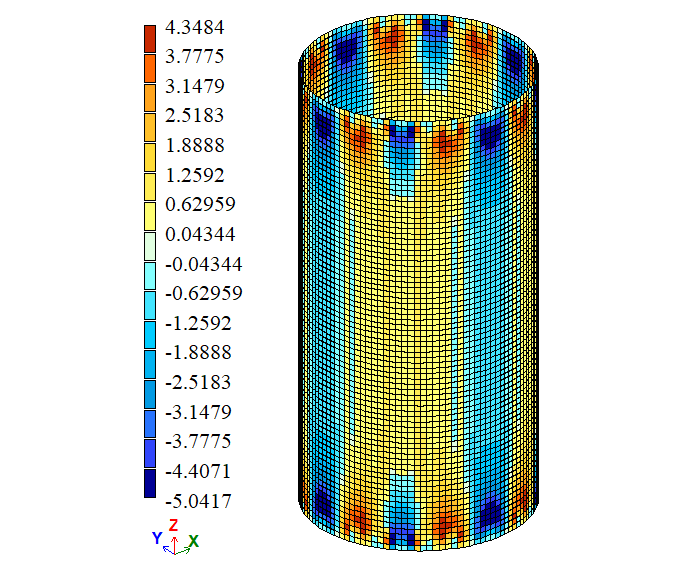
-5,0417 4,3484 |
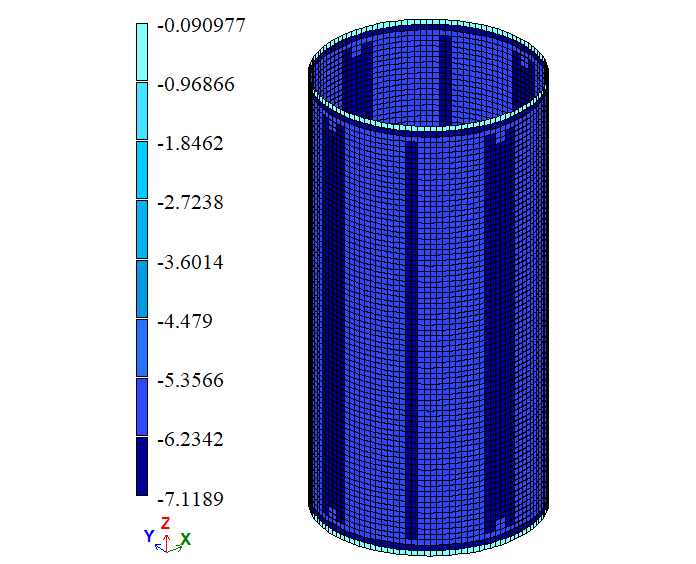
-7,1189 -0,09097 |
- | - | |
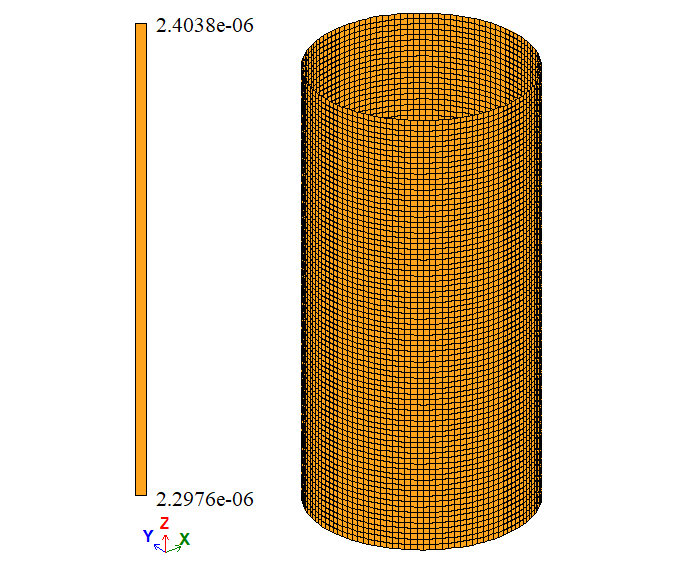
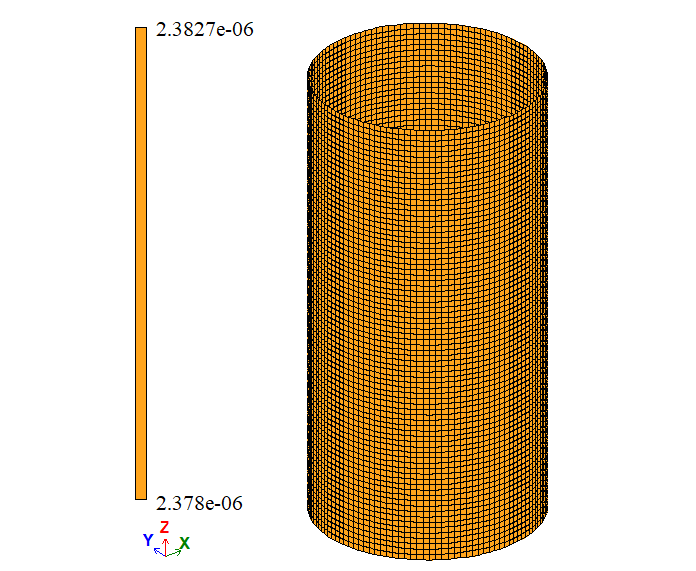
| ΔR, м | 2,38 * 10-6 | 2,3798*10-6 | 2,3803*10-6 | 0,0084 | 0,0126 | |
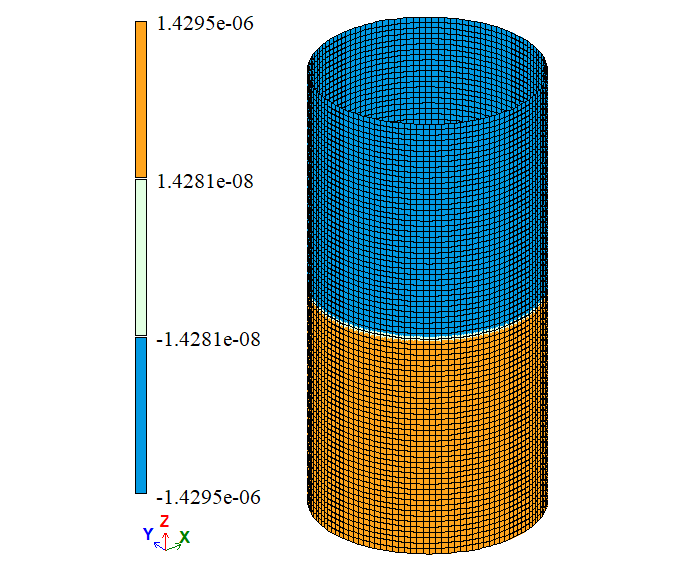
| Δy, м | -2,86 * 10-6 | -2,859 * 10-6 | -2,859 * 10-6 | 0,038 | 0,035 | |
|
Примітка: Оскільки при заданні граничних умов застосовувалися в'язі симетрії (закріплення по Z у середині висоти циліндра), то величина вертикального переміщення Δy в таблиці збільшена у 2 рази. |
||||||
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.

Коментарі