Ціль:
Визначення напружено-деформованого стану круглої пластини.
Література:
S. Timoshenko, Résistance des matériaux, t. 2, Paris, Librairie Polytechnique Ch. Béranger, 1949.
Формулювання задачі:
Визначити вертикальне переміщення Z (w) центра пластини, а також згинальні моменти у жорсткому закріпленні.
Опис розрахункової схеми:
Кругла пластина, затиснена по контуру, завантажена рівномірно розподіленим навантаженням q.
|
а |
б |
Геометрія:
Радіус пластини r = 1,2 м;
Товщина h = 0,02 м;
Характеристика матеріалу:
Модуль пружності Е = 2,0 * 108 кПа;
Коефіцієнт Пуассона ν = 0,3.
Граничні умови:
В'язі по зовнішньому контуру пластини за всіма ступенями вільності СЕ плити (Z, uX, uY).
Навантаження:
Рівномірно розподілене навантаження по площі: q = 10 кПа
Примітка:
Задача розв’язується у плоскій постановці (ознака схеми 3 – площина XOY).
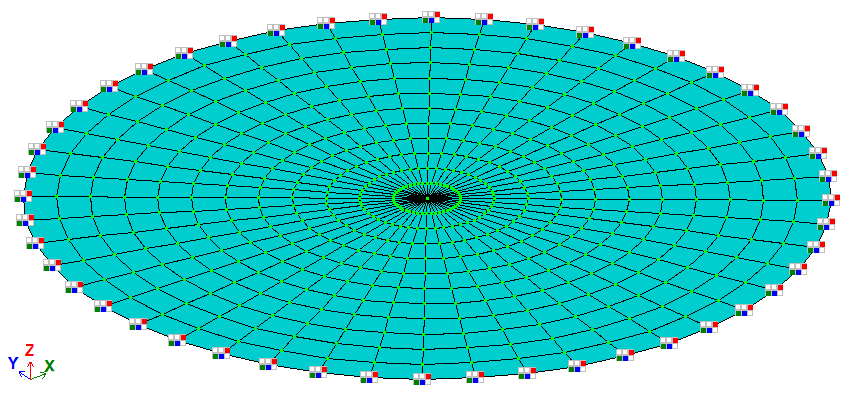
Для побудови схеми використані СЕ 19 – чотирикутний СЕ плити і СЕ 12 – трикутний СЕ плити. Ці СЕ мають три ступені вільності у вузлі – переміщення вздовж глобальної осі Z і повороти навколо глобальних осей uX і uY.
Сітка скінченних елементів має 12 елементів вздовж радіусу і 48 вдовж окружності.
Місцеві осі пластин для результатів узгоджені таким чином, що кожна вісь Y1 напрямлена в центр окружності (вісь Z1 напрямлена вгору).
Кількість вузлів: 577. Кількість елементів: 576.
Результати розрахунку:
|
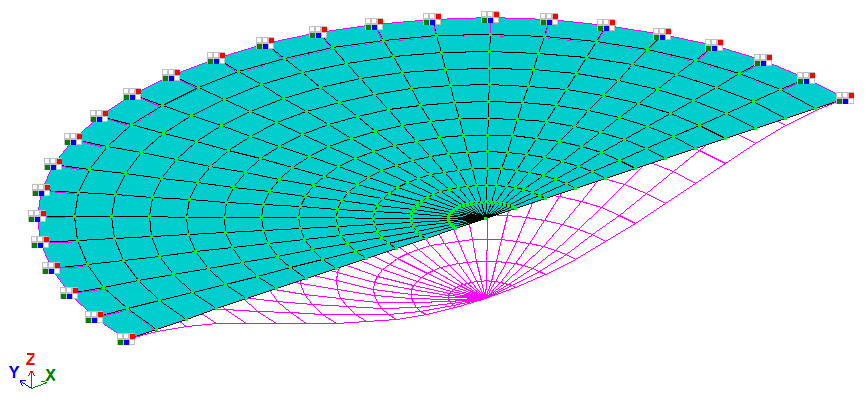
Розрахункова та деформована схеми (показана половина пластини) |
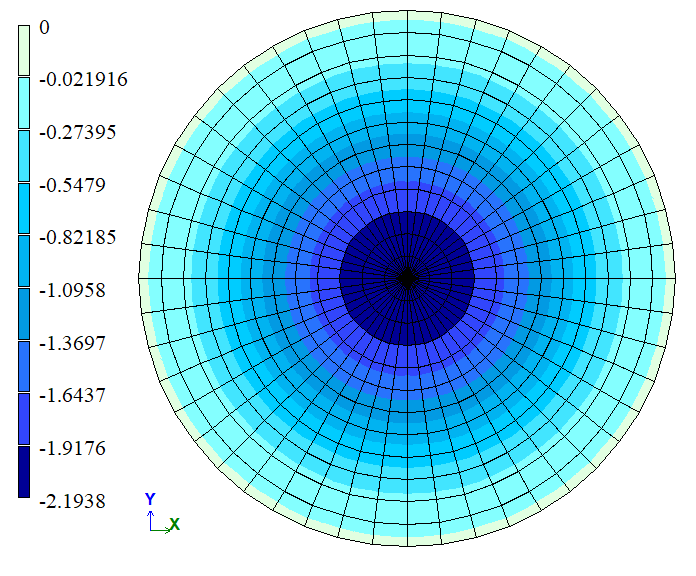
Ізополя вертикальних переміщень Z(w), мм |
|
а |
б |
Аналітичне рішення:
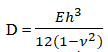
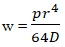
Mx = −qr2/8
My = −vqr2/8
Порівняння результатів розрахунку:
Без додаткових вузлів на сторонах:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| Центр | Переміщення w0, мм | -2,211 | -2,1938 | 0,7779 |
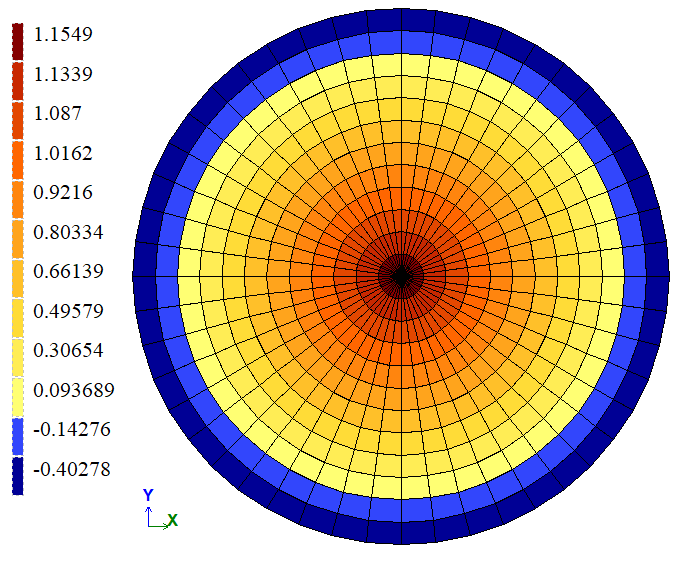
| Край | Згинальний момент Mx, кН*м/м | 1,17 | 1,1549 | 1,2906 |
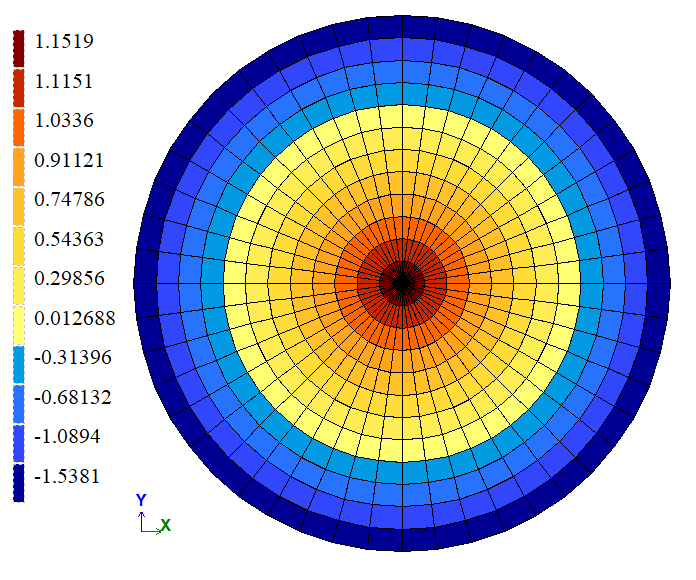
| Згинальний момент My, кН*м/м | 1,17 | 1,1519 | 1,547 |
З використанням додаткових вузлів на сторонах:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| Центр | Переміщення w0, мм | -2,211 | -2,2005 | 0,4749 |
| Край | Згинальний момент Mx, кН*м/м | 1,17 | 1,1619 | 0,6923 |
| Згинальний момент My, кН*м/м | 1,17 | 1,1563 | 1,1709 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.
Коментарі