Ціль:
Визначення напружено-деформованого стану консольної пластини.
Література:
S. Timoshenko, Résistance des matériaux, t. 1, Paris, Librairie Polytechnique Ch. Béranger, 1949.
Формулювання задачі:
Визначити вертикальне переміщення Z(w) вільного краю пластини, а також згинальний момент у жорсткому закріпленні.
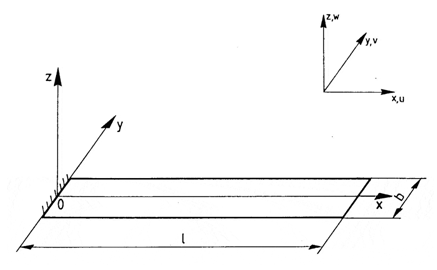
Опис розрахункової схеми:
Консольна пластина, завантажена рівномірно розподіленим навантаженням q.
|
а |
б |
Геометрія:
Товщина пластини h = 0,005 м;
Виліт консолі l = 1 м;
Відносна товщина пластини h/l = 0,005;
Ширина пластини b = 0,1 м.
Характеристика матеріалу:
Модуль пружності Е = 2,1 * 1011 Па;
Коефіцієнт Пуассона ν = 0.
Граничні умови:
В'язі на лівій грані пластини жорстко защемлені за всіма ступенями вільності СЕ плити (Z, uX, uY).
Навантаження:
Рівномірно розподілене навантаження по площі: q = 1700 Па.
Примітка:
Задача розв’язується у плоскій постановці (ознака схеми 3 – площина XOY).
Для побудови схеми використані СЕ 11 – прямокутний СЕ плити. СЕ 11 має три ступені вільності у вузлі – переміщення вздовж глобальної осі Z і повороти навколо глобальних осей uX і uY.
Розмір скінченних елементів: 0,01 × 0,01 м.
Кількість вузлів: 1111. Кількість елементів: 1000.
Результати розрахунку:
|
Ізополя вертикальних переміщень Z(w), м
|
Мозаїка згинальних моментів Мх, Н*м/м
|
Аналітичне рішення:
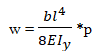
M = −ql2/2
Порівняння результатів розрахунку:
Без додаткових вузлів на сторонах:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| x = 1 | Вертикальне переміщення, м | -0,0973 | -0,0972 | 0,1028 |
| x = 0 | Згинальний момент, Н*м/м | -850 | -842,38 | 0,8965 |
З використанням додаткових вузлів на сторонах:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| x = 1 | Вертикальне переміщення, м | -0,0973 | -0,0972 | 0,1028 |
| x = 0 | Згинальний момент, Н*м/м | -850 | -842,36 | 0,8988 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.




Коментарі