Ціль:
Навантаження балки, затиснутої по кінцях, в одній площині без урахування деформацій поперечного зсуву. Перевіряються значення максимального поперечного переміщення та вигинаючих моментів.
Література:
Писаренко Г.С., Яковлєв А.П., Матвєєв В.В. Довідник з опору матеріалів. — Київ: Наук. думка, 1988.
Формулювання задачі:
Визначити максимальні поперечне переміщення w та вигинаючі моменти M.
Опис розрахункової схеми:
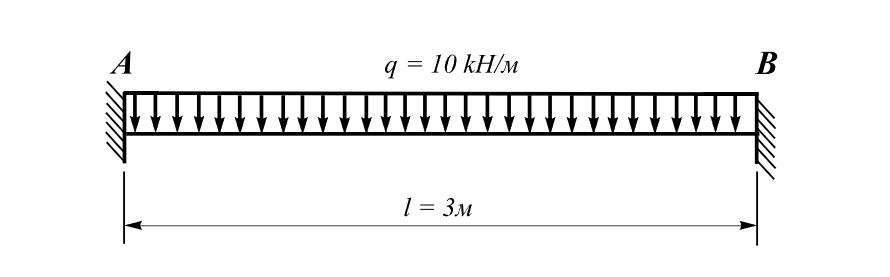
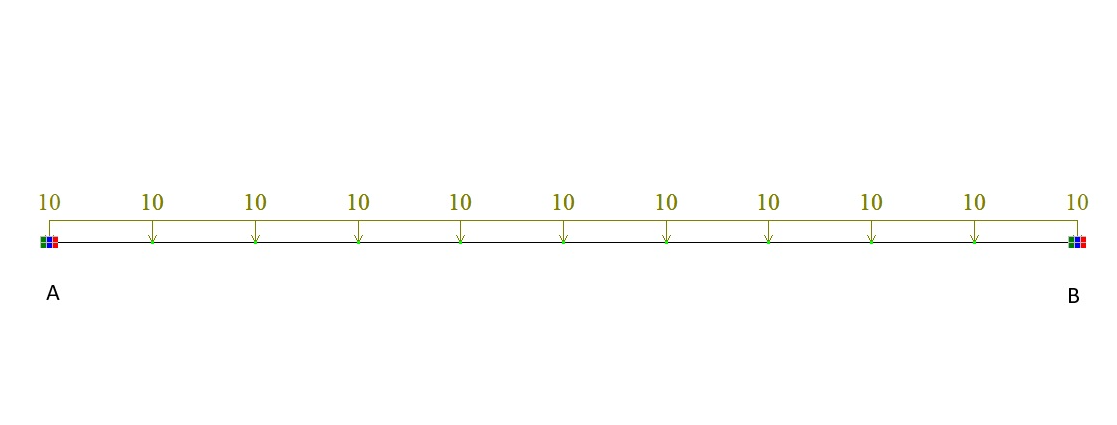
Балка, затиснена по кінцях, навантажується рівномірно розподіленим навантаженням q.
Геометрія:
Довжина балки L = 3 м;
Момент інерції I = 2,44 * 10-6 м4;
Площа поперечного перерізу F = 14,2 * 10-4 м2
Характеристика матеріалу:
Модуль пружності Е = 2,1 * 1011 Па;
Коефіцієнт Пуассона ν = 0,3
Навантаження:
Рівномірно розподілене навантаження q= 10 кН/м.
Примітка:
Розрахункова схема — плоска рама, 10 стержневих елементів типу 2, 11 вузлів.
Результати розрахунку:
Аналітичне рішення:
При аналітичному рішенні прогин в центрі балки може бути обчислений за наступною формулою («Довідник з опору матеріалів» с. 352):
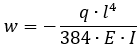
Згинальні моменти в защемленні обчислюються за наступною формулою:
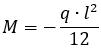
Згинальний момент в центрі балки:
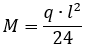
Порівняння результатів розрахунку:
| Параметр | Аналітичне рішення | LIRA-FEM | Похибка, % |
| Вертикальне переміщення в середині прольоту балки, мм | -4,32 | -4,32 | 0 |
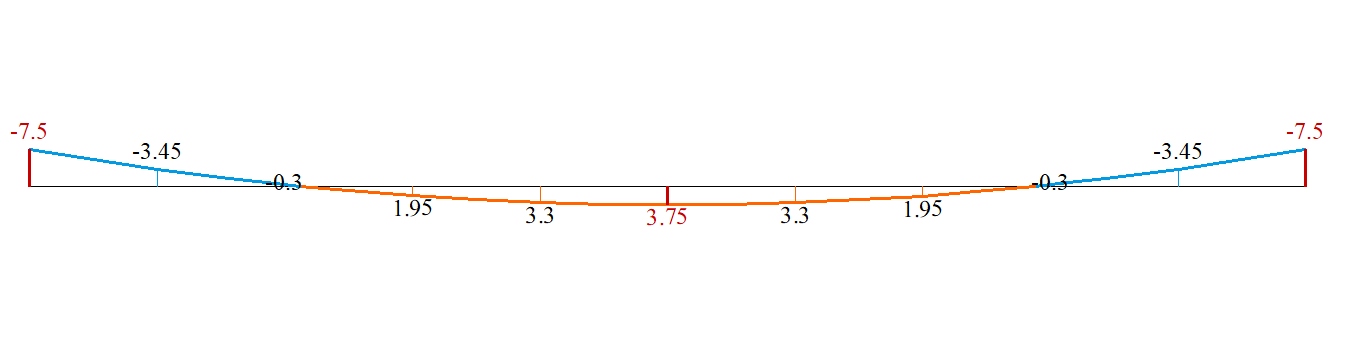
| Згинальний момент в середині прольоту балки, кН*м | 3,75 | 3,75 | 0 |
| Згинальний момент на опорі балки, кН*м | -7,5 | -7,5 | 0 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.

Коментарі