Ціль:
Визначення напружено-деформованого стану балки на пружній основі під дією зосереджених сил і розподіленого навантаження, що змінюється за законом трикутника.
Формулювання задачі:
Визначити вертикальні переміщення Z кінців балки, а також згинальні моменти Мy, поперечні сили Qz і кути повороту uY по її довжині.
Опис розрахункової схеми:
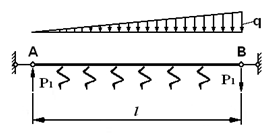
Балка на пружній основі, завантажена взаємо врівноваженими зосередженими силами на кінцях і розподіленим по довжині навантаженням, що змінюється за законом трикутника.
Геометрія:
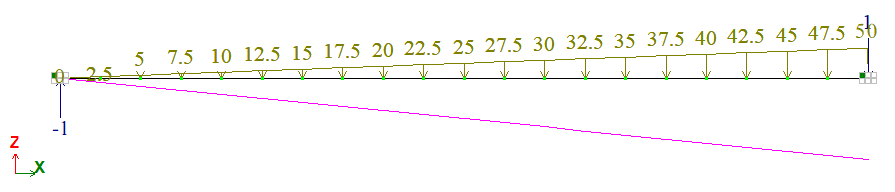
Довжина l = 10 м;
Момент інерції I = 2 * 10-6 м4;
Площа поперечного перерізу A = 0,003 м2;
Зсувна площа F = 0,0025 м2.
Характеристика матеріалу:
Модуль пружності Е = 2,1 * 107 тс/м2;
Модуль зсуву G = 7,875 * 106 тс/м2.
Граничні умови:
Характеристики пружної основи: С1 = 500 тс/м3; С2 = 100 тс/м. В’язі на кінцях балки за ступенями вільності, які забороняють переміщення у напрямку її осі X (uA = uВ = 0).
Навантаження:
Нерівномірно розподілене навантаження: q = 50 тс/м;
Вертикальна зосереджена сила: Р1 = −Р1 = 1 тс.
Примітка:
Задача розв’язується у плоскій постановці (ознака схеми 2 – переміщення X,Z,Uy).
Для побудови схеми використані СЕ 10 – універсальний просторовий стержневий СЕ.
Пружна основа характеризується двома коефіцієнтами постелі (модель Пастернака) прикладеними для ширини лунки осідання Вс = 100 см.
Кількість вузлів: 21. Кількість елементів: 20.
Результати розрахунку:
Аналітичне рішення:
w = −qx / (C1q)
M = 0
Q = −C2q / C1
Порівняння результатів розрахунку:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| А | Переміщення wA, м | 0 | 0 | 0 |
| В | Переміщення wB, м | -0,1 | -0,1 | 0 |
| Будь-яка | Кут повороту θY, рад | 0,01 | 0,01 | 0 |
| Сила Qz, тс | 1 | 1 | 0 | |
| Момент Мy, тс*м | 0 | 0 | 0 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.

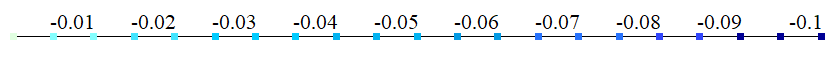

Коментарі