Ціль:
Визначення напружено-деформованого стану призматичного бруса під дією згинального моменту.
Література:
S. Timoshenko, Théorie de l’élasticité, Paris, Librairie Polytechnique Ch. Béranger, 1961, P. 284-289.
Формулювання задачі:
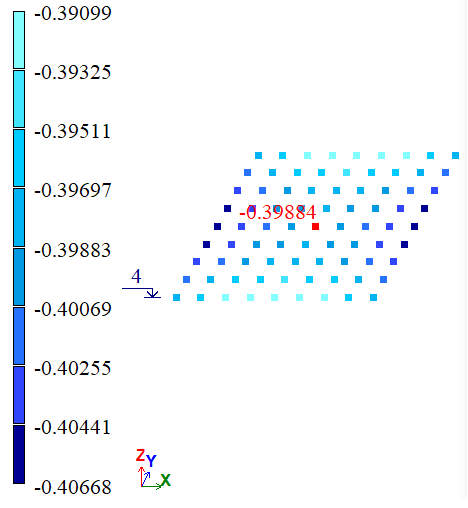
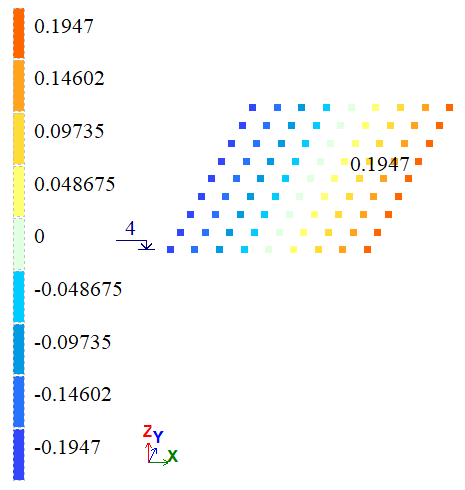
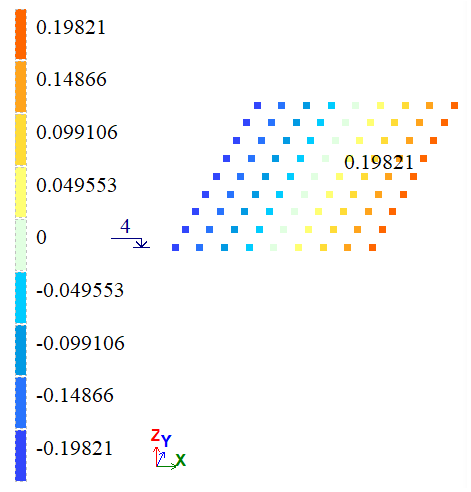
Визначити переміщення по Х в точці А, Z в точці B і по Y в точці D, E, F, G.
Опис розрахункової схеми:
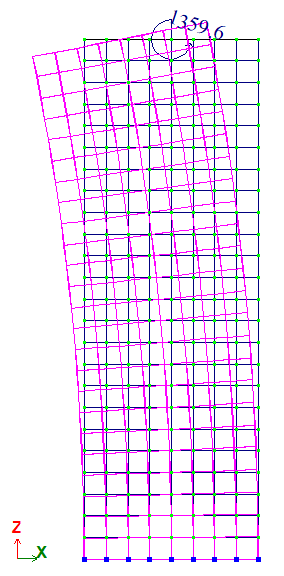
Консольний призматичний брус, завантажений згинальним моментом біля вільного краю.
|
Варіант 1 |
Варіант 2 |
Геометрія:
Довжина l = 6 м;
Розміри перерізу a = b = 1 м;
Ордината контрольного перерізу l′ = (2/3)l = 4 м.
Характеристика матеріалу:
Модуль пружності Е = 2 * 105 МПа;
Коефіцієнт Пуассона ν = 0,3.
Граничні умови:
В’язі за всіма переміщеннями у точці B (X=Y=Z=0).
На площині, що проходить через точку В – в’язі, які забороняють переміщення по Z, та в’язі симетрії.
Навантаження:
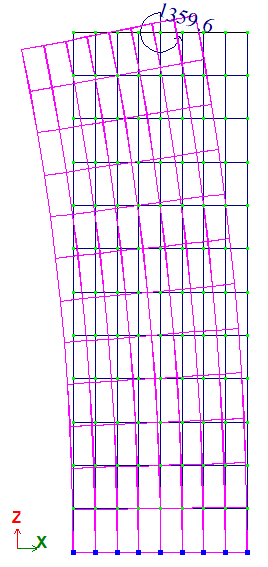
У точці С прикладений момент навколо осі Y, My = 4/3 * 107 Н*м = 1359,62 т*м.
Примітка:
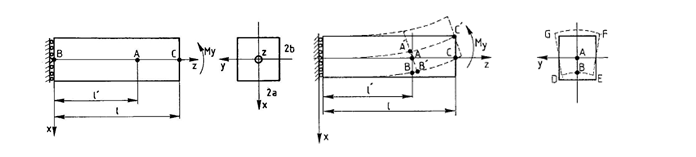
Задача розв’язується у просторовій постановці (ознака схеми 5).
Для побудови схеми використані СЕ 31 – паралелепіпед.
У розрахунковій схемі розглядається вся призма.
Для прикладання моментного навантаження на торець призми був заданий «павук» зі стержневих СЕ 10 (моделювання АЖТ на вигин з площини торця призми і з нульовою жорсткістю в площині, щоб не обмежувати поперечних деформацій, тобто, задана велика згинальна жорсткість із площини перерізу і нульові осьова та згинальна жорсткості у площині перерізу).
Варіант 1:
Сітка 8×8×12.
Кількість вузлів: 1053. Кількість елементів: 944.
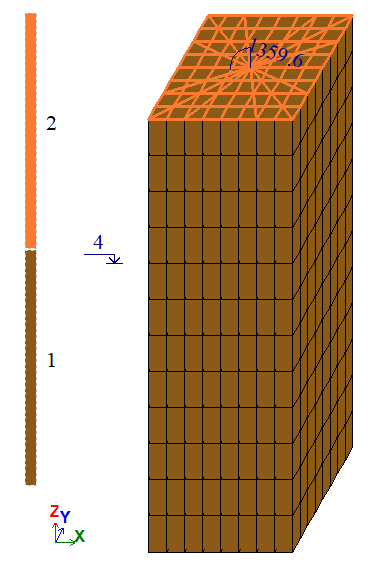
Варіант 2:
Сітка 8×8×24.
Кількість вузлів: 2025. Кількість елементів: 1712.
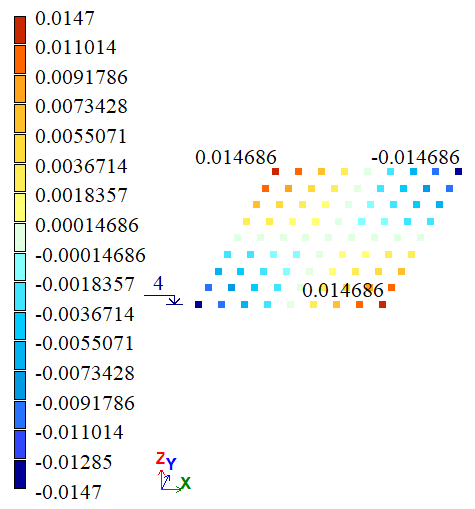
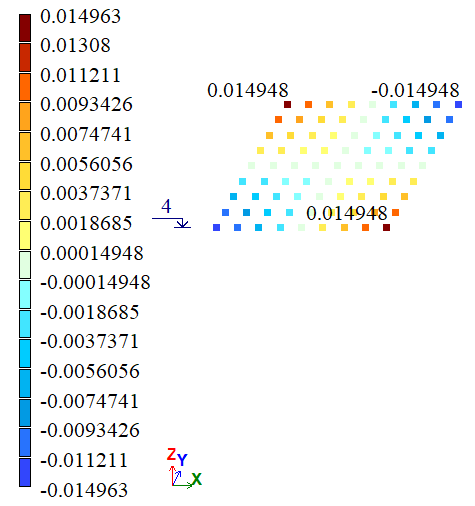
Результати розрахунку:
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
|
Варіант 1 |
Варіант 2 |
Аналітичне рішення:
σxx = σyy = σxy = σyx = σzx = 0
u = -l’2/2R
w = l’2/R
v = ν(a2/R)
Порівняння результатів розрахунку:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % | ||
| Варіант 1 | Варіант 2 | Варіант 1 | Варіант 2 | |||
| А | Х, м | -4*10-4 | -3,9174*10-4 | -3,9884*10-4 | 2,065 | 0,29 |
| А | Х, м | 2*10-4 | 1,947*10-4 | 1,9821*10-4 | 2,65 | 0,895 |
| F, G, D, E | Y, м | 0,15*10-4 | 0,14686*10-4 | 0,14948*10-4 | 2,0933 | 0,3467 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.

Коментарі