Ціль:
Визначення напруженого стану симетричного клину одиничної товщини при згині рівномірно розподіленим навантаженням.
Література:
Демидов С.П. Теория упругости, М., Высшая школа, 1979.
Формулювання задачі:
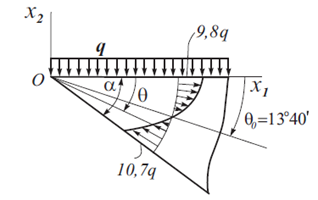
Визначити напруження в клині σrr на відстані r = 5 м від вершини для вигину клину рівномірно розподіленим навантаженням, а також кут θ0 при якому σrr=0.
Опис розрахункової схеми:
До верхньої грані клину одиничної товщини прикладено рівномірно розподілене навантаження інтенсивністю q.
|
а |
б |
Геометрія:
Товщина клину h = 1 м;
Радіус, що обмежує область клину R = 15 м;
Кут при вершині клину 2α = 30°.
Характеристика матеріалу:
Модуль пружності Е = 3 * 107 кПа;
Коефіцієнт Пуассона ν = 0,2.
Граничні умови:
В’язі за всіма ступенями вільності по контуру дуги клину.
Навантаження:
Рівномірно розподілене навантаження: q = 10 кН/м
Примітка:
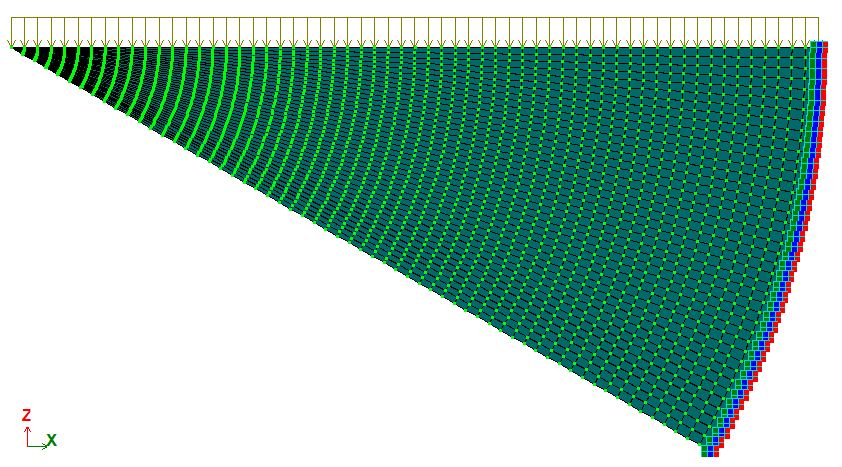
Задача розв’язується у просторовій постановці (ознака схеми 5).
Для побудови схеми використані СЕ 44 – універсальний чотирикутний СЕ оболонки і СЕ 42 – універсальний трикутний СЕ оболонки.
Сітка скінченних елементів має 60 елементів вздовж радіусу і 40 вдовж окружності.
Місцеві осі пластин для результатів узгоджені таким чином, що кожна місцева вісь Y1 напрямлена до вершини клину.
Кількість вузлів: 2461. Кількість елементів: 2400.
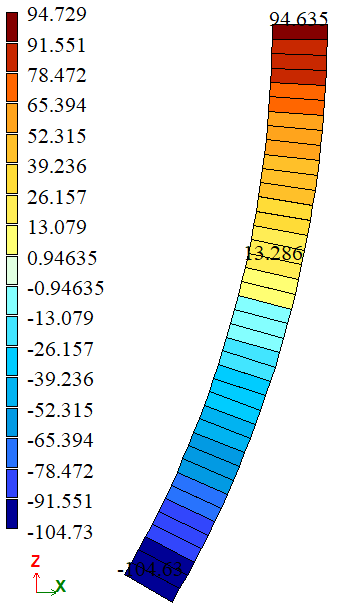
Результати розрахунку:
|
а |
б |
Аналітичне рішення:
K = tgα-α
σrr = q(2α-2θ-(1-cos2θ)*tgα)-sin2θ)/2K
σθθ = q(2α-2θ-(1+cos2θ)*tgα)+sin2θ)/2K
σrθ = q(1-tgα*sin2θ-cos2θ)/2K
Порівняння результатів розрахунку:
Без додаткових вузлів на сторонах:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| r = 5 м при θ = 0 | Ny, кН/м2 | 98 | 94,635 | 3,4337 |
| r = 5 м при θ = α | Ny, кН/м2 | -107 | -104,63 | 2,215 |
| σrr = 0 | θ0, ° | 13,4 | 14,25 | 5,9649 |
З використанням додаткових вузлів на сторонах:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| r = 5 м при θ = 0 | Ny, кН/м2 | 98 | 94,974 | 3,0878 |
| r = 5 м при θ = α | Ny, кН/м2 | -107 | -104,97 | 1,8972 |
| σrr = 0 | θ0, ° | 13,4 | 14,25 | 5,9649 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.


Коментарі