Ціль:
Визначення напружено-деформованого стану просторової стержневої системи з пружними в'язями під дією зосередженої сили.
Література:
M. Laredo, Résistance des matériaux, Paris, Dunod, 1970, P. 165.
Формулювання задачі:
Визначити вертикальне переміщення Z для вузла з’єднання стержнів AD і HD (точка D), горизонтальне переміщення та кут повороту точки А, а також крутний і згинальні моменти Mx, My, Mz для вузлів закріплення просторової системи (точки А, В).
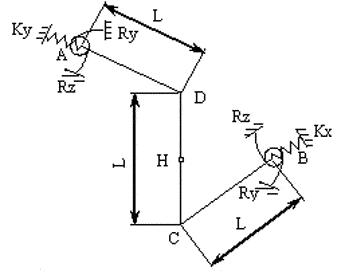
Опис розрахункової схеми:
Просторова система складається з чотирьох стержнів. Горизонтальні стержні ортогонально лежать у паралельних горизонтальних площинах і з'єднані вертикальними стержнями, які шарнірно з’єднуються між собою (точка Н).
В опорних вузлах просторової системи (точки А, В) встановлені жорсткі в'язі за напрямками лінійних та кутових ступенів вільності в площині поперечного перерізу та пружні в'язі за напрямками лінійного та кутового ступенів вільності з площини поперечного перерізу.
У вузлі з’єднання верхнього горизонтального та вертикального стержнів (точка D) прикладена вертикальна зосереджена сила F.
|
а |
б |
Геометрія:
Довжина горизонтальних стержнів L = 2 м;
Довжина вертикальних стержнів 0,5L = 1 м;
Моменти інерції перерізу Iy = Ix = I = 10-6 м4;
Полярний момент інерції (постійна кручення) J = 2 * 10-6 м4;
Площа перерізу A = 0,001 м2.
Характеристика матеріалу:
Модуль пружності Е = 2,1 * 1011 Па;
Модуль зсуву G = 7,875 * 1010 Па.
Граничні умови:
У точці А: жорсткі в’язі за напрямками ступенів вільності uY (θY=0), X і Z (uA=wA=0);
в’язі скінченної жорсткості за напрямками ступенів вільності Y, uX, uZ: Rу = 52500 Н/м, Rux = Ruz = 52500 Н*м/рад.
У точці В: жорсткі в’язі за напрямками ступенів вільності uX (θX=0), Y і Z (uB=wB=0);
в’язі скінченної жорсткості за напрямками ступенів вільності X, uY, uZ: Rх = 52500 Н/м, Ruy = Ruz = 52500 Н*м/рад.
У точці Н: шарнір.
Навантаження:
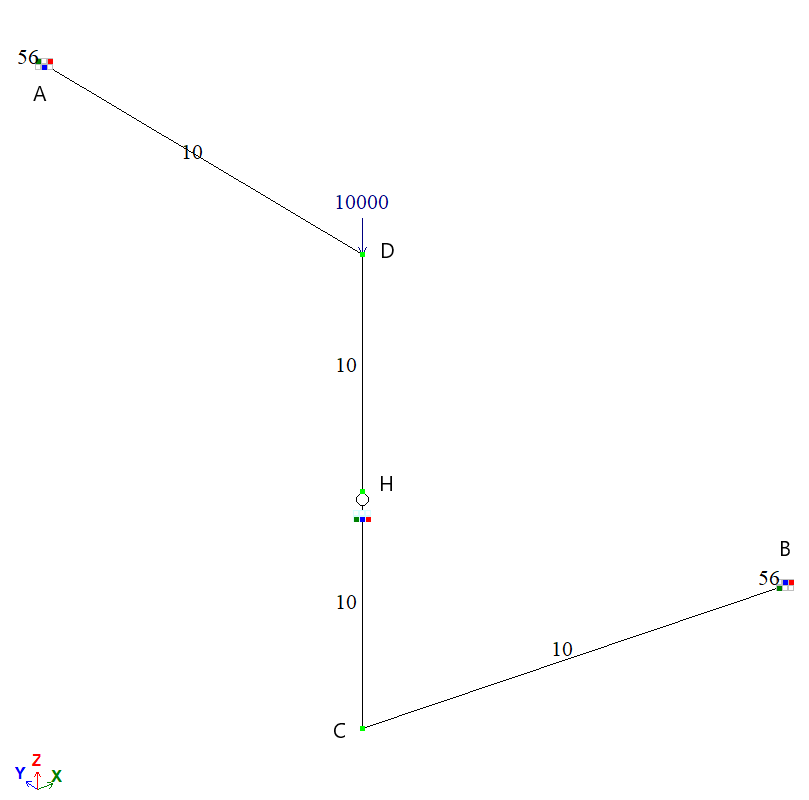
Вертикальна зосереджена сила F = 10000 Н, прикладена в точці D.
Примітка:
Задача розв’язується у просторовій постановці (ознака схеми 5).
Для побудови схеми використані CЕ 10 – універсальний просторовий стержневий CЕ.
В'язі скінченної жорсткості в точках А і В задані за допомогою CЕ 56 – одновузловий CЕ пружних в'язей.
У точці Н стержня CD введено шарнір за напрямками ступенів вільності uY, uX, uZ.
Кількість вузлів: 5. Кількість елементів: 6.
Результати розрахунку:
|
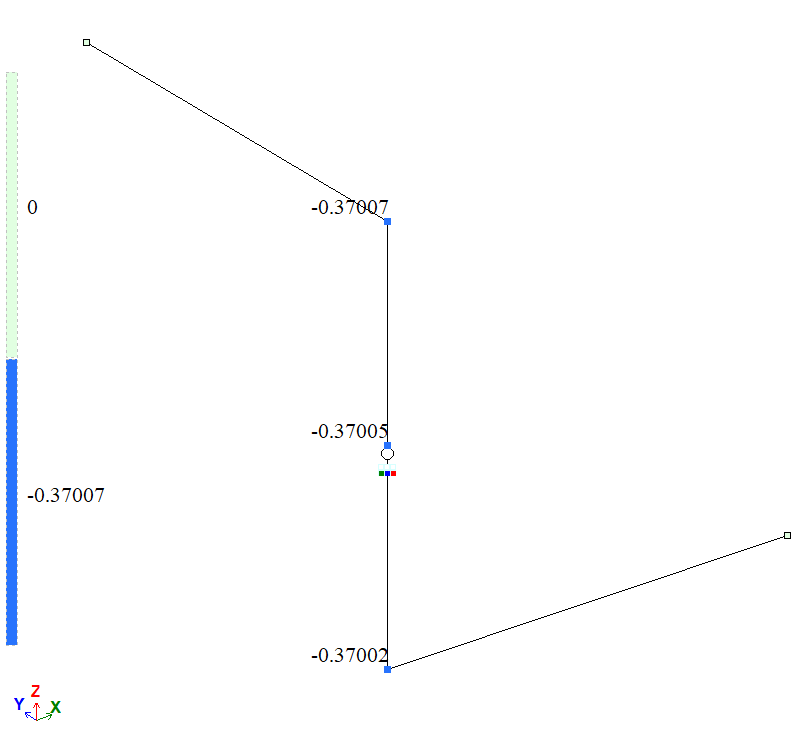
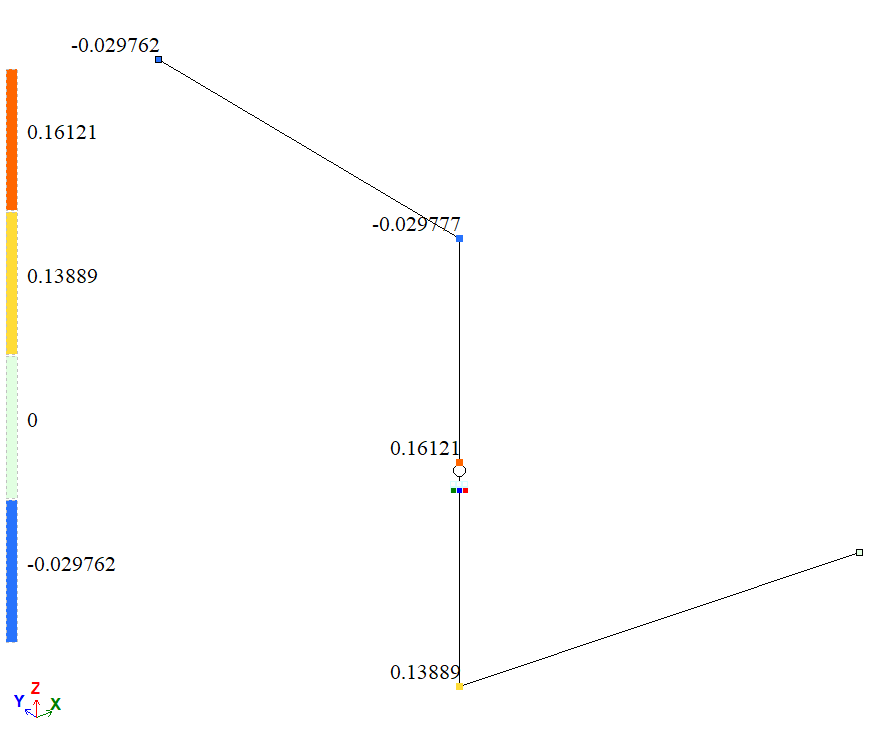
Мозаїка вертикальних переміщень вздовж глобальної осі Z (w), м
|
Мозаїка горизонтальних переміщень вздовж глобальної осі Y (v), м
|
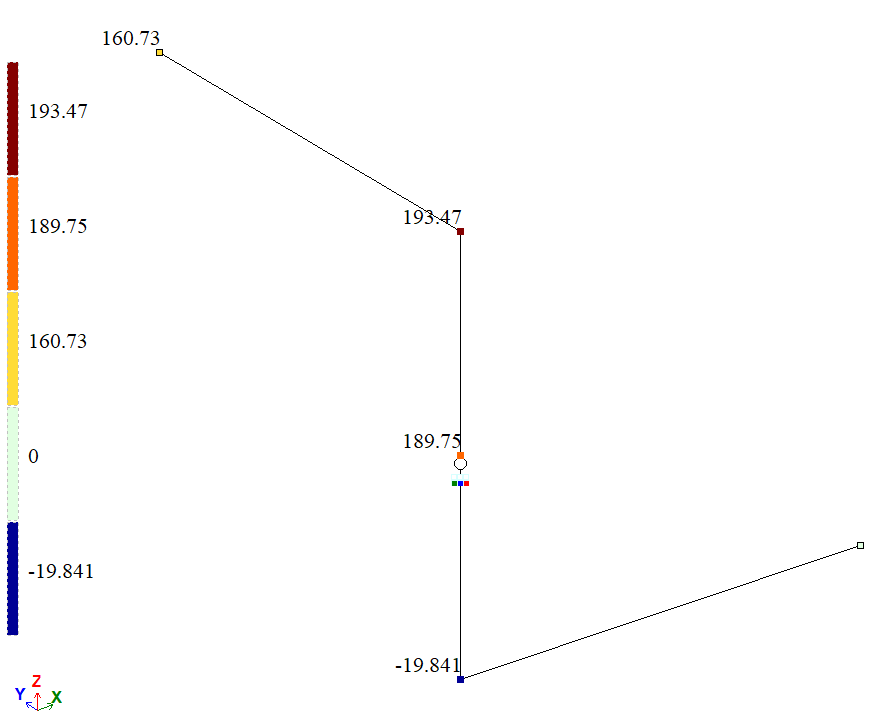
Мозаїка кутів повороту навколо глобальної осі Х (u), рад*1000
|
|
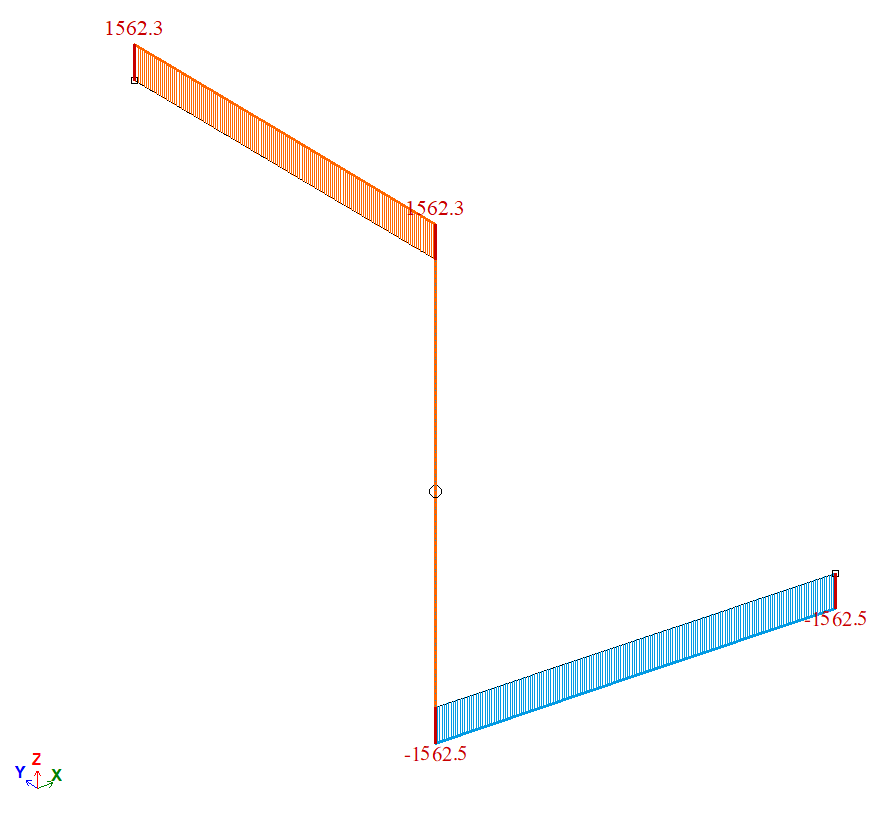
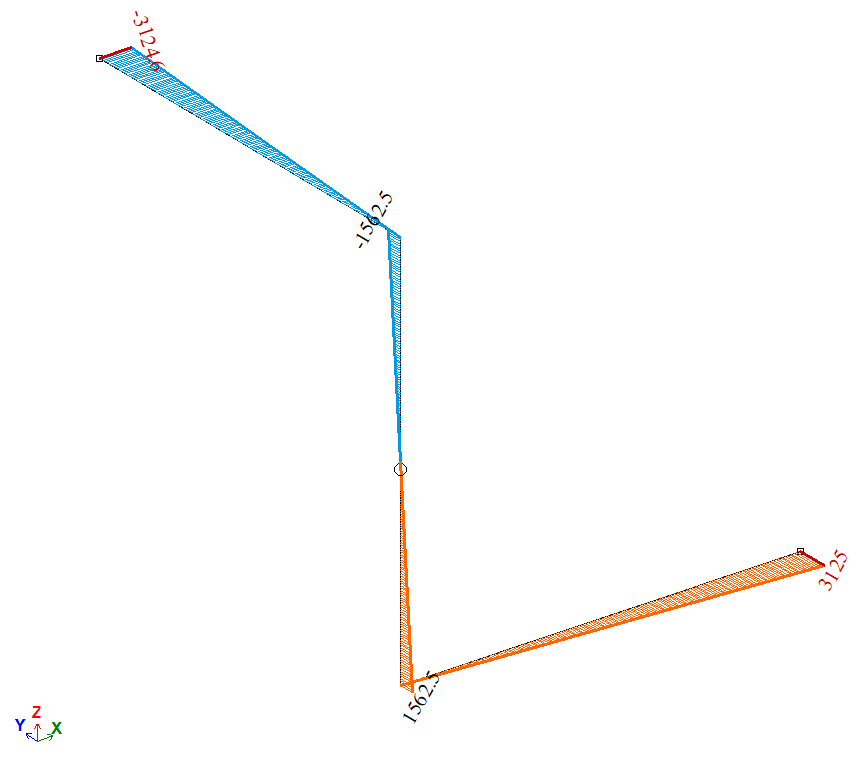
Епюра крутних моментів Мх, Н*м
|
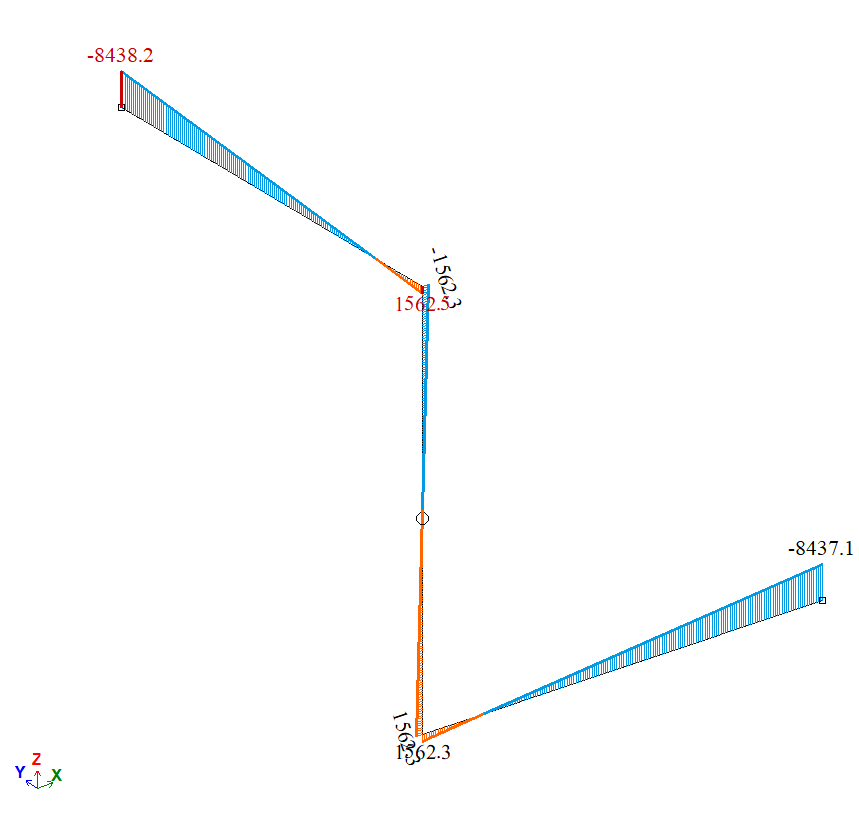
Епюра згинальних моментів Му, Н*м
|
Епюра згинальних моментів Мz, Н*м
|
Аналітичне рішення:
MAx = 5*F*l/64
MAy = 27*F*l/64
MAz = -5*F*l/32
MBx = -27*F*l/64
MBy = -5*F*l/64
MBz = -5*F*l/32
νA = 5*F*l/(64*EI)
θAx = -27*F*l2/(32*EI)
ωD = 373*F*l3/(384*EI)
Порівняння результатів розрахунку:
| Точка | Шукана величина | Аналітичне рішення | LIRA-FEM | Похибка, % |
| А | Момент Мх, Н*м | 1562,5 | 1562,3 | 0,0128 |
| А | Момент Му, Н*м | 8437,5 | 8438,2 | 0,083 |
| А | Момент Мz, Н*м | 3125 | 3124,6 | 0,0128 |
| B | Момент Мх, Н*м | 1562,5 | 1562,5 | 0 |
| B | Момент Му, Н*м | 8437,5 | 8437,1 | 0,0047 |
| B | Момент Мz, Н*м | 3125 | 3125 | 0 |
| А | Переміщення νA, м | 0,02976 | 0,02977 | 0,001 |
| А | Кут повороту θAX, рад | 0,16071 | 0,16073 | 0 |
| D | Переміщення ωD, м | 0,37004 | 0,37007 | 0,0027 |
Завантажити приклад
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.
Коментарі