Можливості застосування суперелементів під час вирішення різних завдань будівельної механіки

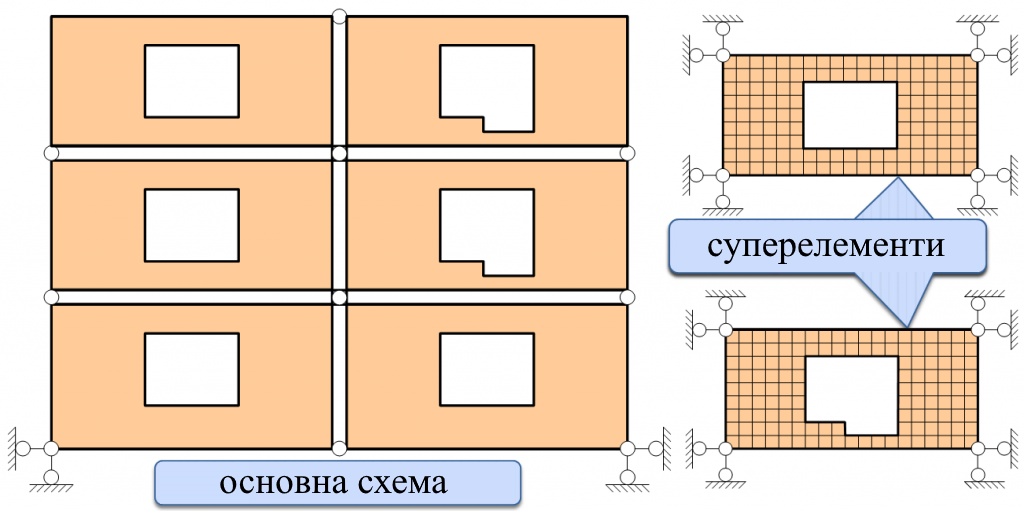
Якщо система, що розраховується, занадто громіздка, то іноді виявляється зручним організувати рекурсивний розрахунок з розчленуванням всієї системи на підсистеми - суперелементи. Цей прийом може виявитися вдалим, коли розчленування на підсистеми відбувається природно: наприклад, будівля з об'ємних блоків (об'ємний блок - суперелемент) або діафрагма висотної будівлі, що збирається з окремих панелей (панель - суперелемент). Фрагмент діафрагми висотного будинку показаний на рис. 1а. Діафрагма складається з окремих панелей, що з'єднуються між собою у кутових точках.

Розрахунок такої системи можна виконати звичайним способом: нанести необхідну сітку і розрахувати всю систему повністю. Однак велика кількість розрахункових вузлів, елементів, невідомих переміщень може дуже ускладнити вирішення задачі.

Використовуючи суперелементи, можна провести розрахунок поетапно, суттєво зменшивши на кожному етапі розмірність задачі.

Спочатку побудувати матрицю жорсткості для всіх типів суперелементів (у даному випадку є два типи (рис. 1б), потім розрахувати систему, що складається із суперелементів (в даному випадку система складатиметься з 6 суперелементів із 12 супервузлами). Внаслідок цього розрахунку будуть визначені переміщення супервузлів. На заключному етапі розрахувати кожен із шести суперелементів на задані переміщення супервузлів та місцеве навантаження.

Послідовність розрахунку системи, набраної з суперелементів, аналогічна звичайній процедурі МКЕ з тією різницею, що матриця жорсткості та приведення місцевого навантаження до вузлового визначаються не на основі апроксимуючих функцій МКЕ, а чисельним методом. Оскільки суперелемент представляє сам по собі досить складну систему, то матриці апроксимуючих функцій будуються за допомогою чисельного розрахунку суперелементу на поодинокі зміщення супервузлів, в результаті якого будується матриця впливу, що зв'язує переміщення внутрішніх вузлів суперелементу з поодинокими зміщеннями супервузлів. Така процедура обробки суперелементів дозволяє представити метод суперелементної рекурсії як розрахунок по методу скінченних елементів з побудовою апроксимуючих функцій за допомогою матриць впливу.

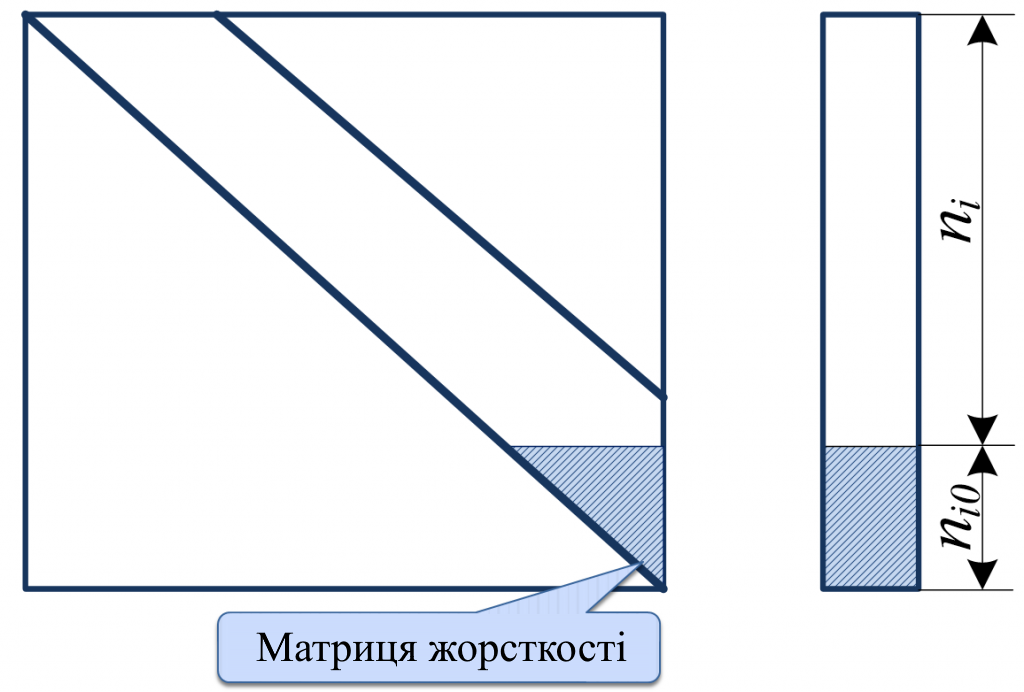
Інша процедура обробки суперелементів [3], заснована на тому, що у фізичному сенсі виключення j невідомого за Гаусом відповідає визволенню від j в'язі. Це призводить до такої схеми побудови матриці жорсткості та зведення місцевого навантаження до вузлового: для i суперелементу спочатку нумеруються всі внутрішні вузли (відповідне їм число ступенів свободи позначимо n_i), а потім супервузли (кількість ступенів свободи, що відповідає супервузлам, позначимо n_i0); складаються канонічні рівняння для всіх n_i+n_i0 ступенів свободи (риc. 2); виключаються n_i невідомі; частини матриці, що залишилися, і стовпці вільних членів (на рис. 2 вони заштриховані) утворюють шукані матриці жорсткості та стовпці вузлових навантажень у супервузлах суперелементу, до яких приведене місцеве навантаження, прикладене по області суперелементу.

Можна побудувати обчислювальний процес розчленовування суперелементів на суперелементи другого рангу і т. д. організувавши багаторангову рекурсію МСЕ.

Основні ідеї методу суперелементів (МСЕ) були вперше викладені у роботі Пржемініцького [1]. Ідеї Пржемініцького отримали свій розвиток у роботі Мейснера [2], який надав їм формалізований вигляд та узагальнив на кілька рівнів поділу (багаторангова рекурсія МСЕ). Подальшому розвитку МСЕ присвячено низку більш пізніх робіт [3-12].

Якщо проводити математичні аналогії, то МСЕ віддалено нагадує блочний Гаус, а багаторангова рекурсія МСЕ - сучасний метод вкладених перерізів для вирішення розріджених матриць, однак, як і МКЕ, метод суперелементів заснований на безпосередній дискретизації розрахункової моделі. У цьому сенсі МСЕ має велику наочність, він природний і нагадує процес збирання конструкції з секцій і блоків.

МСЕ дуже ефективний у ряді випадків, наприклад:

• при вирішенні великорозмірних задач, що містять однакові в сенсі топології суперелементи. Тут значно скорочується кількість обчислень, тому що матриця жорсткості для однакових суперелементів будується лише один раз;
• при розрахунку конструктивних схем, де нелінійність локалізована у деякій області;
• при побудові матриці жорсткості елементів з істотною зміною жорсткістних характеристик по області елементу, викликаних або нелінійністю, або конструктивними особливостями (стержень із змінним перерізом по довжині);
• при побудові матриці жорсткості елементів, що взаємодіють з більшерозмірним середовищем і примикають до основної конструктивної схеми одним вузлом (наприклад, паля в ґрунтовому масиві).

Розрахунок конструктивної схеми, що включає однакові суперелементи

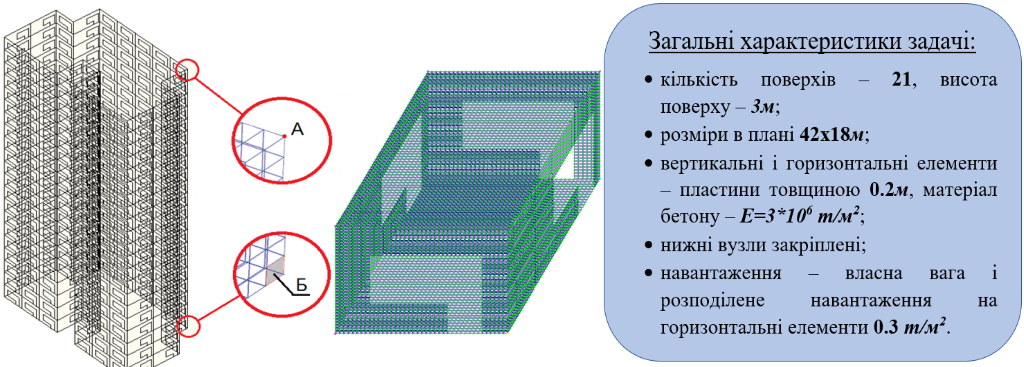
Розрахункова схема представлена на рис. 3

Розрахунок виконувався програмним комплексом ЛІРА-САПР на комп'ютері Pentium Core i7 (8 ядер), 16 GB.

Було виконано два розрахунки (використовувалися прямокутні скінченні елементи пластин) без застосування суперелементів та із застосуванням суперелементів.

Розрахункова схема для першого розрахунку містила 3771744 елементів, 3850650 вузлів, 19421820 невідомих. Розрахункова схема для другого розрахунку містила 378 суперелементів. Кожен суперелемент включав 660 вузлів.

Порівняння результатів за двома розрахунками наведено в табл. 1.

Таблиця 1

Наведений приклад демонструє значне збільшення швидкості розв'язання задачі (див. табл.1). Цим не вичерпується переваги МСЕ – значно полегшується підготовка вихідних даних до аналізу результатів, але, мабуть, найбільш важливою перевагою МСЕ є підвищення точності розв'язання задачі. При великій розмірності задачі та великому розкиді величин жорсткістних характеристик погіршується обумовленість задачі і накопичуються помилки округлення, що в ряді випадків може призвести до неправильних результатів. МСЕ у цих випадках є дієвим інструментом для боротьби з «прокляттям» розмірності, яке властиве більшості чисельних методів, включаючи і МКЕ.

Розрахунок конструкцій із локалізованою областю нелінійності

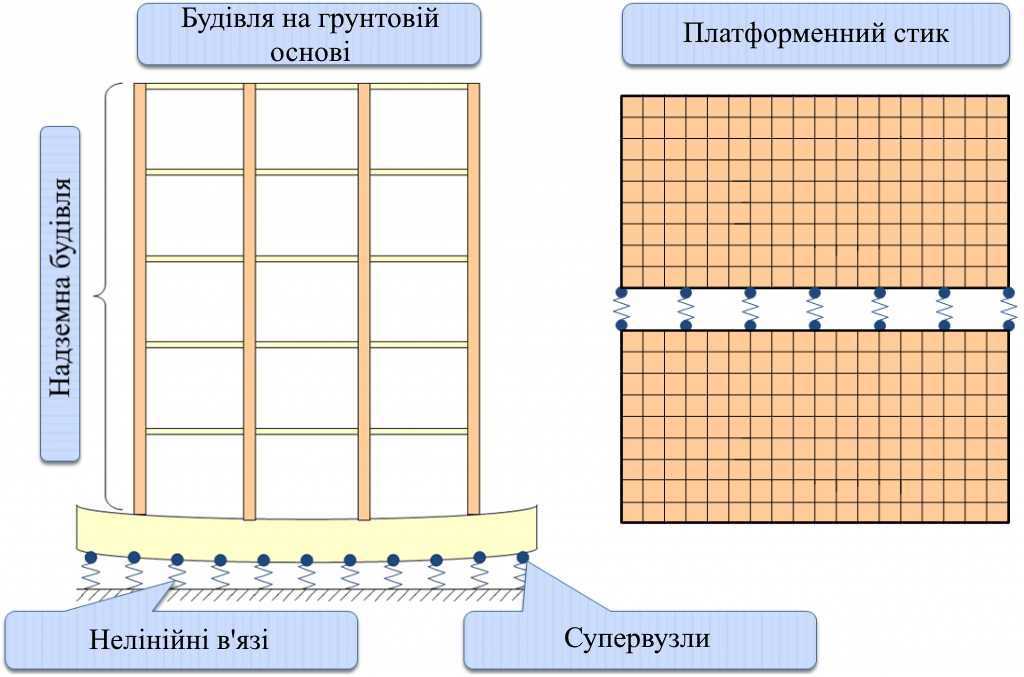
На рис. 4 схематично представлена розрахункова схема конструкції, що представляє надземну будову, яка спирається на систему в'язів, що мають суттєву нелінійність. Сама надземна будова в рамках заданої точності може розраховуватись у лінійній постановці. Розрахункова схема надземної будови може містити велику кількість вузлів та елементів та включення її в нелінійний розрахунок, обумовлений суттєвою нелінійністю в'язів обумовить великий час розв'язання задачі. В цьому випадку доцільно оголосити розрахункову модель надземної будови суперелементом і вирішувати нелінійну задачу тільки для основної схеми, що включає супервузли (на рис.4,а позначені жирними точками) та нелінійні в'язі.

Такий же прийом може бути використаний при побудові розрахункової схеми панельної будівлі з платформними стиками панелей (рис. 4, б).

Збірні панелі при експлуатаційному навантаженні практично працюють у лінійно пружній стадії і нелінійність роботи всієї конструкції зосереджується в локальних областях платформних стиків. Тому, вводячи в розрахункову схему панелі у вигляді суперелементів, можна значно скоротити час розв'язання нелінійної задачі.

Застосування МКЕ для побудови матриць жорсткості стержня, що має змінний переріз по довжині

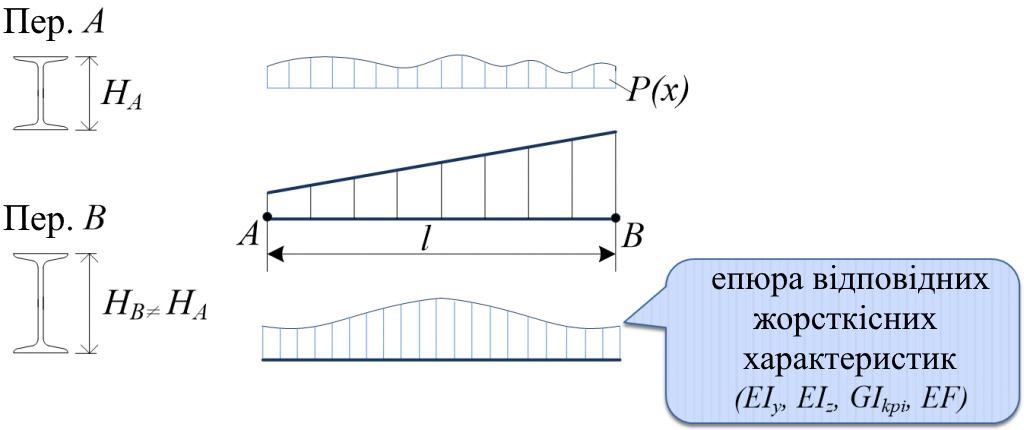
Змінна жорсткість по довжині стержня перерізу може бути обумовлена змінною висотою стінки або змінними ширинами полиць чи іншими конструктивними особливостями. У цих випадках побудова залежності зміни жорсткості по довжині стержня, для того, щоб аналітично побудувати матрицю жорсткості, може викликати значні труднощі, тим більше, що ці залежності для EIz, EIy, EF, GI_кp як правило різні.

Можна ввести в розрахункову схему такі стержні з численними проміжними вузлами, однак це призводить до значного збільшення розміру задачі, ускладнює складання вихідних даних та аналіз результатів. У цьому випадку зручним виявляється застосування МСЕ (рис. 5).

Стержень розбивається по довжині на n ділянок. Вузли А та В оголошуються супервузлами. По схемі (рис. 2) проводиться побудова матриць жорсткості стержня та приведення місцевого навантаження до вузлового.

В результаті розв'язання всієї системи визначається переміщення вузлів А та В. У разі необхідності визначення переміщень у внутрішніх вузлах елементу виконується зворотний хід для стовпців вільних членів – див. рис. 2, де n_io – знайдені переміщення супервузлів А та В, а потім і зусилля по довжині стержня.

Застосування МСЕ для побудови матриці жорсткості стержня для нелінійних задач

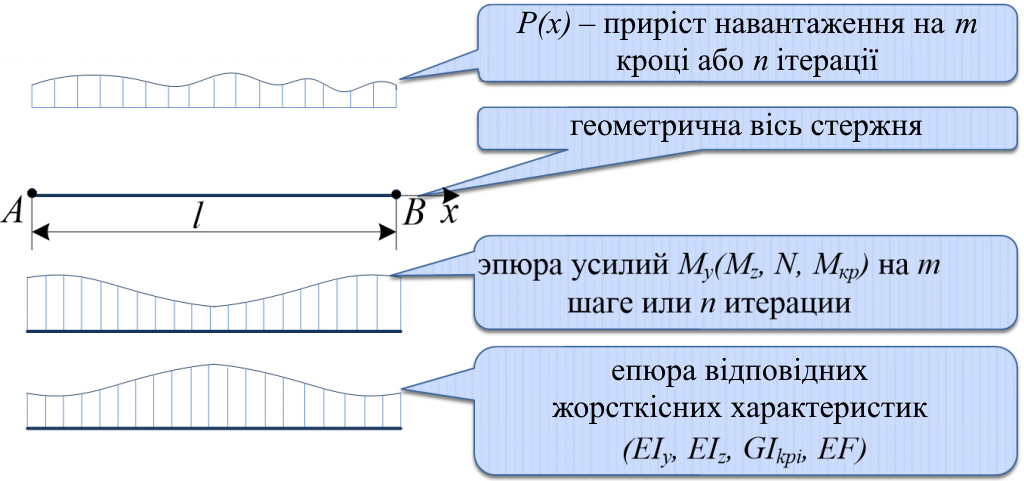
При розв'язанні задач з урахуванням фізичної нелінійності важливою процедурою є побудова матриці жорсткості стержня на m кроці або на n ітерації. Зміна зусиль по довжині стержня обумовлює зміну жорсткістних характеристик перерізів (рис. 6).

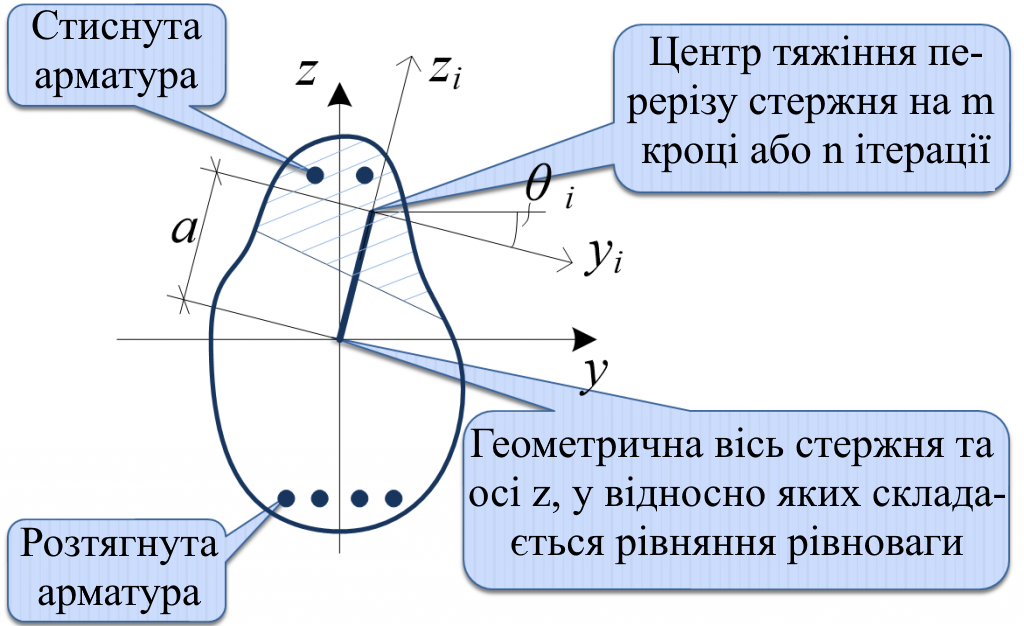
Складність задачі посилюється ще й тим, що центр ваги жорсткістних характеристик зміщується відносно геометричної осі стержня, відносно якої складаються та розв'язуються рівняння рівноваги (рис. 7).

Тому кожен i переріз має не тільки властиві йому на m кроці або на n ітерації жорсткістні характеристики (EI_yi, EI_zi, GI_кpi, EF_is, GI_кpi), але й абсолютно жорстку вставку a_i и угол чистого вращения θ_i.

Щоб врахувати ці ефекти необхідно по довжині стержня вводити проміжні вузли, що різко збільшує розмірність розв'язуваної задачі. У цьому випадку доцільно застосувати МСЕ аналогічно до описаної вище процедури для стержня зі змінним перерізом по довжині.

Застосування МСЕ для побудови матриці жорсткості палі у ґрунтовому масиві

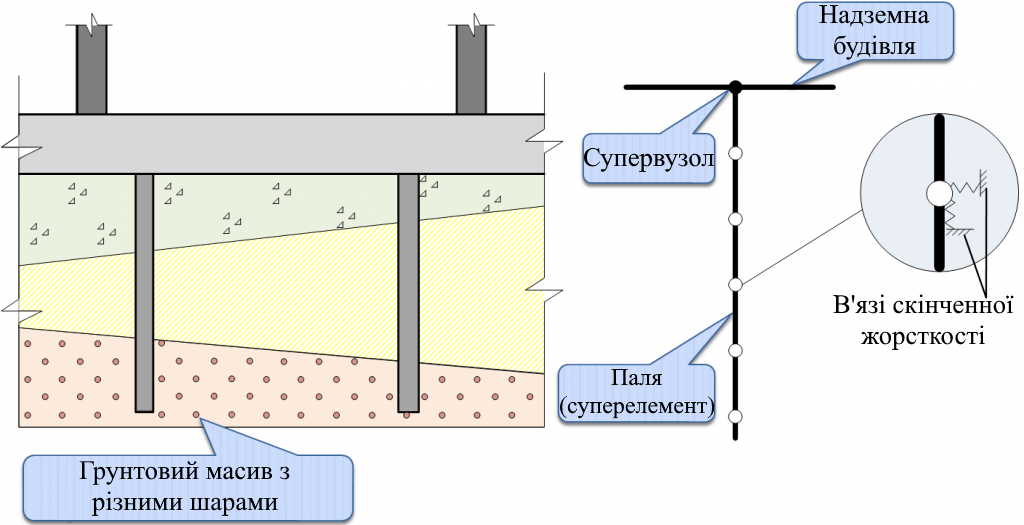
Взаємодія палі з ґрунтовим масивом (рис.8) може бути змодельована введенням по довжині палі додаткових вузлів і введення в ці вузли в'язів кінцевої жорсткості по трьох напрямках. Такий підхід обумовлює різке збільшення розмірності задачі, оскільки необхідно в розрахункову схему включити надземну будову, фундаментну конструкцію, ґрунтовий масив та стержні (палі) з великою кількістю проміжних вузлів.

У цьому випадку доцільним є застосування МСЕ. Стержень (паля) має один супер вузол примикання палі до надземної будови. Побудова матриці жорсткості аналогічна суперелементній процедури для стержня змінної жорсткості з тією лише різницею, що в проміжних вузлах крім жорсткістних характеристик власне стержня враховуються жорсткістні характеристики в'язів кінцевої жорсткості, які примикають, що враховує взаємодію з відповідним шаром ґрунту.

У цьому випадку при розв'язанні задачі взаємодії надземної будови з ґрунтовим масивом моделюється введення в'язів лише у супервузлах і відпадає необхідність включення в розрахункову схему ґрунтового масиву.

Реалізація МСЕ представляється досить складною, на території колишнього СРСР МСЕ був реалізований у програмному комплексі КАСКАД [10] програмному комплексі МІРАЖ [11] та всіх подальших програмних комплексах сімейства ЛІРА, включаючи сучасні версії ЛІРА-САПР.

Література

1. Пржеминицкий Е. С. Матричный метод исследования конструкций на основе анализа подструктур. – Ракетная техника и космонавтика, 1963, №1.
   
2. Мейснер К. Алгоритм многосвязного объединения для метода жесткостей структурного анализа. – Ракетная техника и космонавтика, 1968, № 11.
   
3. Городецкий А. С. Численная реализация метода конечных элементов. – В кн.: Сопротивление материалов и теория сооружений. – Киев: Будивельник, 1973, вып. XX.
   
4. Городецкий А. С. Вычислительный комплекс для расчета строительных конструкций на ЭВМ «МИНСК-32». – В кн.: Организация, методы и технология проектирования, 1976, вып. 9.
   
5. Nagy L. I. Static Analysis Via Substructuring of an Experimental Vehicle Front – End Body Structure: Intern. Conf. on Vehicle Structural Mechanics: Finite Element Application to Vehicle Design – Detroit, Michigan,1974 ( March).
   
6. Neke I., Nagai K., Fuke H. General Purpose Program of Plane Stress Analysis by Finite Element Method and its Application. – IHI Engineering Rev., 1972, vol. 5, No.1.
   
7. Araldesen P. O., Roren E. M. Q. The finite Element Method using Superelements. The SESAM – 69 Struct. – In: Conf. on Modern Techniques of Ship Struct. Analysis and Design. – Berkley: University of California, 1970 (September).
   
8. Метод суперэлементов в расчете прочности судовых конструкций/ В. А. Постнов, С. А. Дмитриев, Б. К. Елтышев, А. А. Родионов. – Судостроение, 1975, №11.
   
9. Постнов В. А. , Родионов А. А., Ценков М. Ц. Метод суперэлементов в линейных и нелинейных задачах. – В кн.: Метод конечных элементов в строительной механике. – Горький: Изд-во ГГУ, 1975.
   
10. Постнов В. А., Дмитриев С. А., Елтышев Б. К., Родионов А. А. Метод суперэлементов в расчетах инженерных сооружений. – Л.: Судостроение, 1979.
    
11. Городецкий А. С. Программа «Мираж» для статического расчета конструкций методом конечных элементов, Сборник трудов Всесоюзной конференции «Автоматизация проектирования, как комплексная проблема совершенствования проектного дела в стране». – М.: 1973.
    
12. Городецкий А. С. Возможности применения суперэлементов при решении различных задач строительной механики/ Александр Сергеевич. Городецкий // Строительная механика и расчет сооружений. – 2015 – № 4. – С. 51-56
    

• суперелемент
• матриця жорсткості
• паля
• платформенний стик
• нелінійність