
Розглядаються різні види конструктивної нелінійності. Особлива увага приділяється проблемі односторонніх в'язів. Наводиться універсальний алгоритм розрахунку систем, що включають односторонні в'язі. Наводиться розв'язання деяких задач, для яких відомі методи не призводять до необхідного результату.
Конструктивна нелінійність обумовлюється властивістю окремих елементів конструкції включатися в роботу в залежності від різних факторів напружено-деформованого стану:
- зусилля в елементі – елемент працює тільки на стиснення або розтягування;
- елемент вмикається в роботу після вибору зазору;
- елемент вимикається з роботи після досягнення будь-яких факторів (наприклад, після досягнення граничного зусилля).
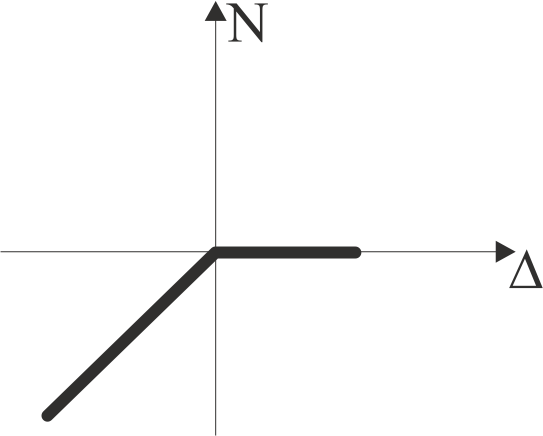
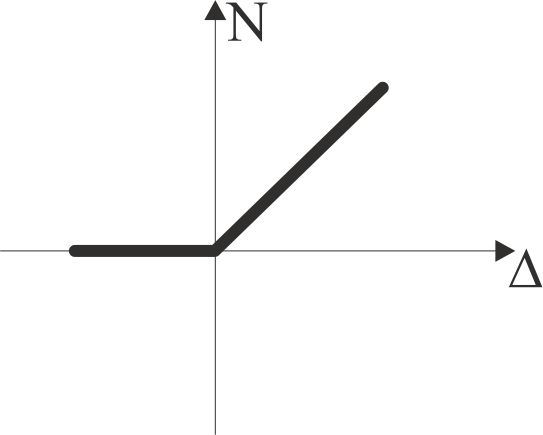
Конструктивна нелінійність може бути зведена до нелінійної залежності між зусиллями та переміщеннями (рис. 1, 2):
|
|
|
а) |
б) |
|
Рис. 1. Залежності N – Δ для різних типів конструктивної нелінійності: а) елемент працює тільки на стиснення; б) елемент працює лише на розтягування
|
|
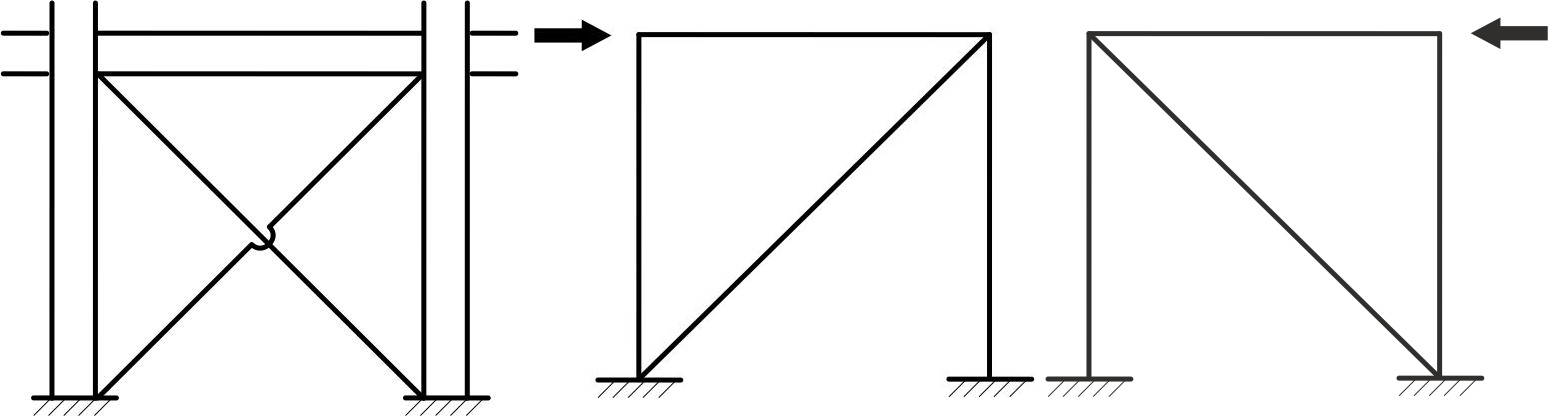
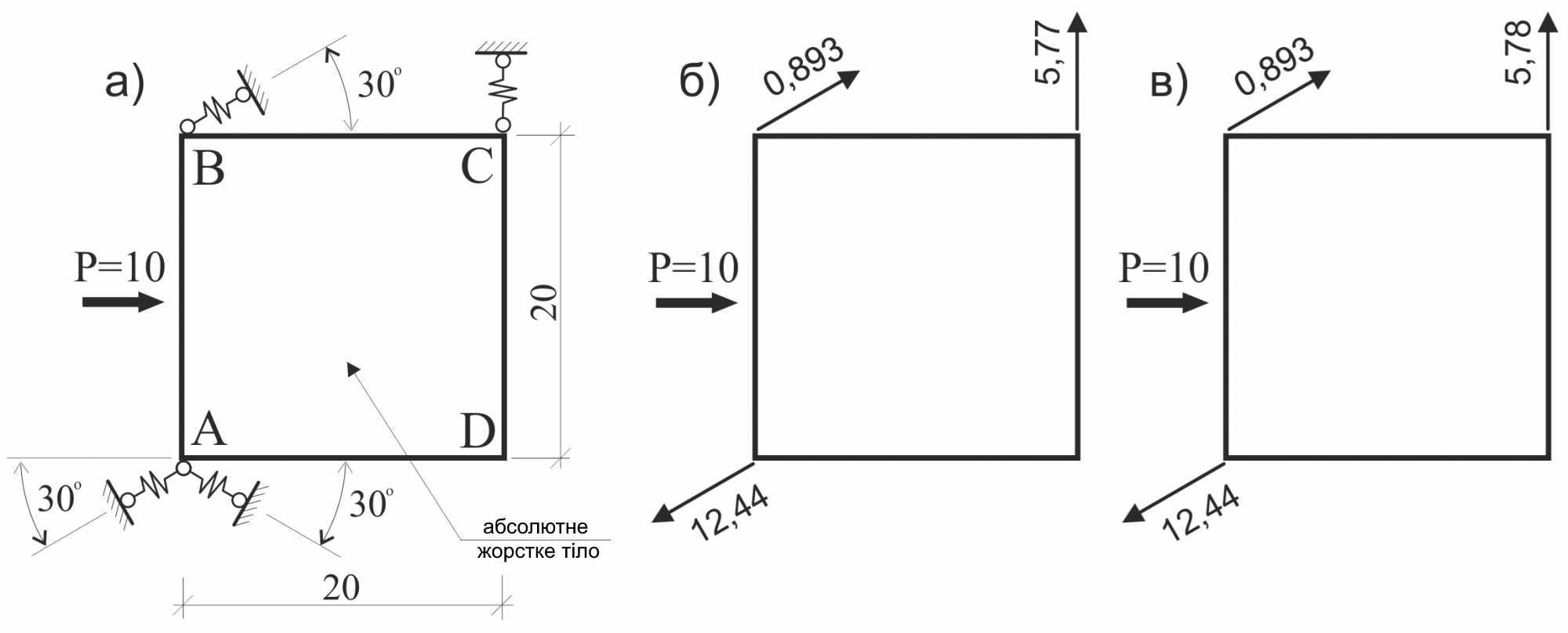
На рис. 3 а наведено приклад вертикальних в'язів по колонах промислових цехів виконаних у вигляді двох тяжів, що не перетинаються, які сприймають тільки розтягуючи зусилля. Тому різним напрямкам горизонтального навантаження відповідають різні розрахункові схеми (рис. 3 б, 3 в).
Залежність N – Δ для тяжів у цьому випадку буде відповідати рис. 1 б.
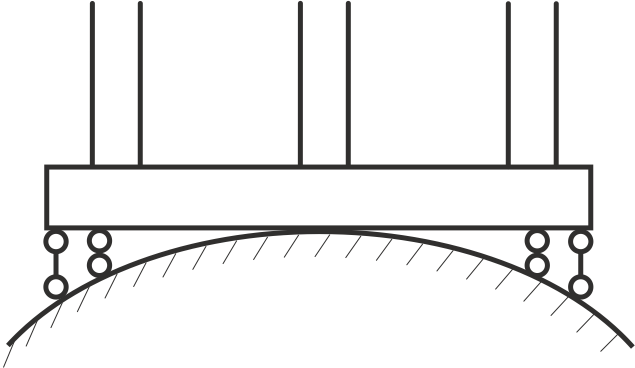
На рис. 4 представлена схема характерна для задач розрахунку будівель на територіях, що підробляються. У міру обтиснення ґрунту в роботу включатимуться нові ділянки ґрунту. Залежність N – Δ у цьому випадку буде відповідати рис. 2 б.
Цю задачу можна віднести до класу контактних задач, які часто зустрічаються у будівельній практиці.
на підроблюваних територіях
На рис. 5 представлена схема характерна для фундаментів під висотні конструкції (вежі, труби, опори ЛЕП, фундаменти під опори вітроагрегатів та ін.).
Конструкції фундаментів у таких випадках необхідно перевіряти на відрив. Залежність N – Δ для елементів моделюючих ґрунтову основу відповідає рис. 1 а.
висотних споруд
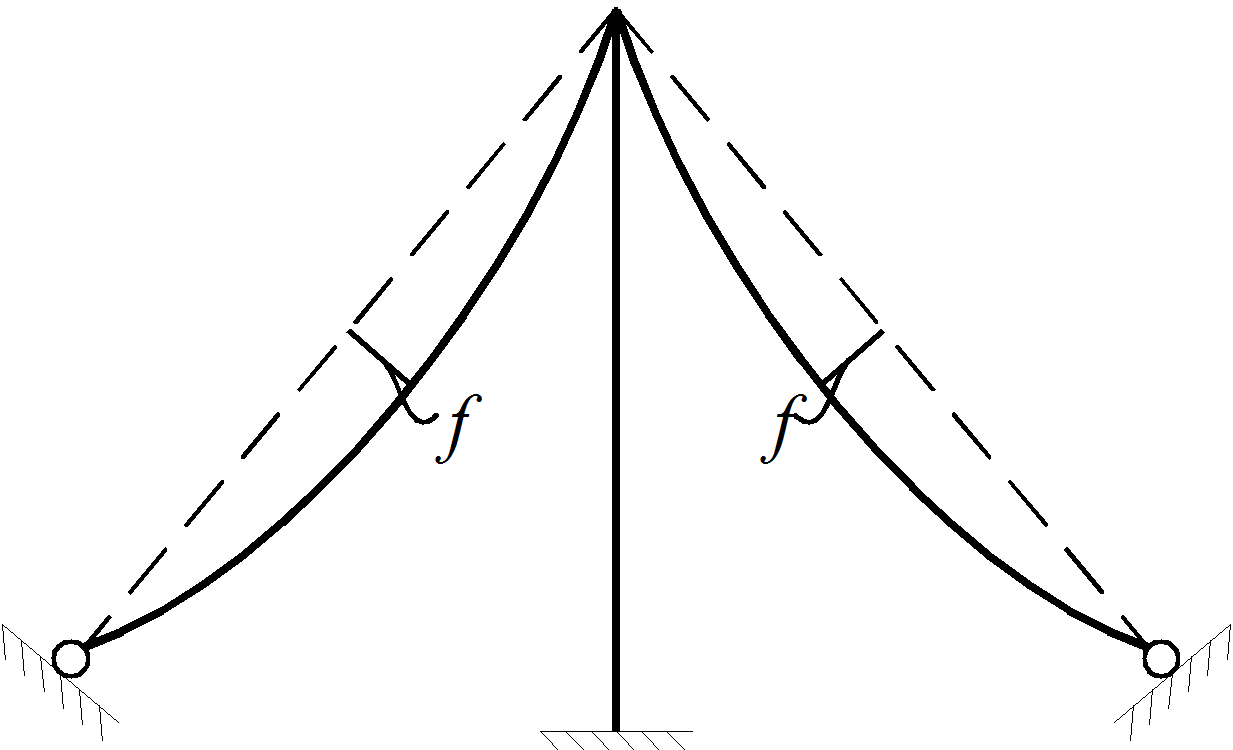
На рис. 6 представлена схема характерна для конструкцій щогл із вантами. Ванти працюють тільки на розтягнення і включаються в роботу після певного зменшення провису f. Залежність N – Δ у цьому випадку буде відповідати рис. 2 а. Наявність попереднього натягу, який практично завжди присутній у конструкціях такого типу, дещо пом'якшує, але не виключає цей ефект. Попереднє натяг обумовлює також можливість роботи вант на певну величину стискаючого зусилля, приблизно рівну величині попереднього натягу. Після досягнення цієї величини ванта виключається з роботи.
Залежність N – Δ у цьому випадку відповідає рис. 2 г. У ПК ЛІРА-САПР для вирішення задач подібного типу реалізовано кроковий метод.
Задачі з односторонніми в'язями також відносяться до класу задач конструктивної нелінійності.
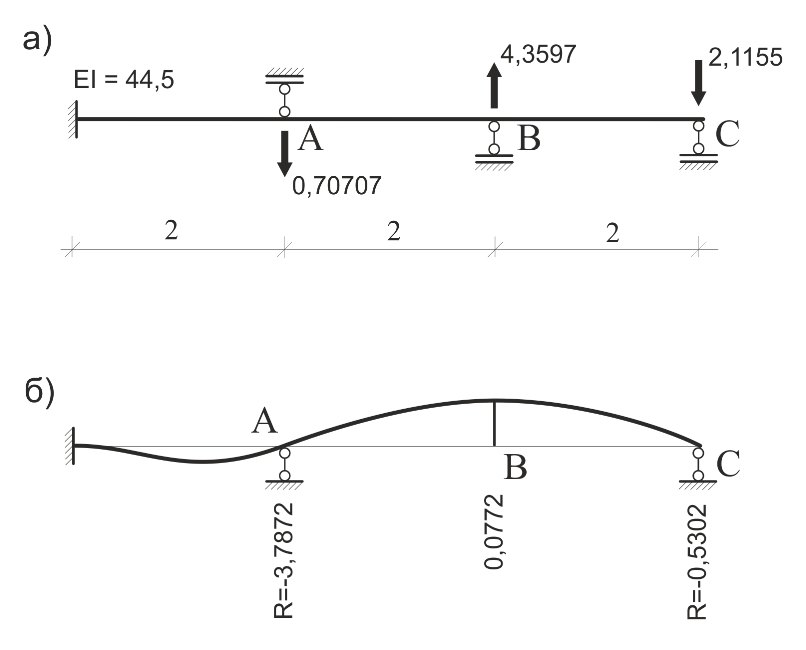
Проблема розрахунку систем з односторонніми в'язями (рис. 1 а, б) є досить складною і їй приділялася та приділяється багато уваги [1, 2, 3, 4, 5]. Найбільш природний метод [1] розрахунку полягає у проведенні ряду ітерацій, де на кожній наступній ітерації виключаються в’язі з неприпустимими зусиллями, отриманими на попередній ітерації. Такий спосіб нерідко призводить до зациклювання, тобто в’язі то включаються, то вимикаються і шлях до знаходження усталеної правильної остаточної схеми не може бути знайдений. У роботі [3] наведений приклад найпростішої схеми (рис. 7) – всі в’язі А, В, С працюють тільки на стиснення - для якої наведений вище метод призводить до зациклювання.
У ПК ЛІРА-САПР реалізовано чисельний ітераційний метод вирішення подібних задач. В основу покладено модифікований метод компенсуючих навантажень. На відміну від реалізацій у застарілому процесорі попередніх версій, у ПК ЛІРА-САПР відбувається автоматичний вибір кількості ітерацій залежно від заданої точності. Критерієм досягнення заданої точності є квадратична нев'язка між реакціями у в'язях на n+1 та n ітераціях.
Користувач на власний розсуд сам може призначити кількість ітерацій. У табл. 1 наведено результати розрахунку схеми (рис. 7) в залежності від кількості ітерацій.
Таблиця 1
|
Параметри розв'язуваної задачі |
Точне рішення |
Кількість ітерацій |
||
|
2400 |
10000 |
30000 |
||
|
Реакція А |
3,7872 |
– 3,83 |
– 3,795 |
– 3,7871 |
|
Реакція С |
0,5302 |
– 0,52 |
– 0,527 |
– 0,5301 |
|
Переміщення В |
0,0772 |
0,0778 |
0,0773 |
0,0772 |
У роботі [4] наведено схему (рис. 8) – всі в'язі працюють тільки на розтягнення – яка при використанні методу [1] таїть ще одну (крім зациклювання) неприємність: вже після першої ітерації схема перетворюється на геометрично змінювану, і подальший розрахунок без будь-яких хитрощів неможливий.
На рис. 8 наведено розв'язання задачі ітераційним методом (300 ітерацій), яке практично співпадає з точним рішенням. Елемент ABCD моделюється абсолютно жорстким тілом. ПК ЛІРА-САПР допускає застосування у розрахункових схемах довільних абсолютно жорстких тіл з необмеженою кількістю провідних вузлів. Вирішення великої кількості практичних задач ітераційним методом жодного разу не призводило до тупикових ситуацій. Таким чином, можна зробити обережний висновок, що є універсальний алгоритм та програма для вирішення довільних систем з односторонніми в'язями.
б – точне рішення; в – рішення, отримане ітераційним методом
Література
- Рабинович И. М. Некоторые вопросы теории сооружений, содержащих односторонние связи // Инженерный сборник – М. –Л.: Издательство АН СССР, 1950.– Т.VI.
- Гордеев В.И., Перельмутер А.В. Расчет упругих систем с односторонними связями, как задача квадратичного программирования // Исследования по теории сооружений. – М.:Стройиздат, 1966. – Вып. 15
- Перельмутер A. B. Элементы теории систем с односторонними связями // Обзоры по вопросам проектирования металлических конструкций. – М.: ЦИНИС Госстроя СССР, 1969. – Вып. 3. – 127 с.
- Перельмутер А. В., Сливкер В. И. Расчётные модели сооружений и возможность их анализа– М.: Издательство АСВ, 2011. – 709 с.
- Вовкушевский A. B., Шойхет Б. А. Расчет массивных гидротехнических сооружений с учетом раскрытия швов — М.: Энергоиздат, 1981. – 136 с.
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.





Коментарі