Загальні принципи
При розв'язанні задачі теплопровідності невідомою є температура у вузлах розрахункової схеми (аналогічно переміщенням у міцністній задачі). Тоді Рівняння рівноваги виглядає:
Задача теплопровідності


Міцністні задачі


Матриця теплопровідності формується з коефіцієнтів теплопровідності К, що задаються в жорсткості скінченного елементу. У випадку пластин, матриця теплопровідності множиться на товщину елементу Н.
При вирішенні нестаціонарної задачі теплопровідності до рівняння рівноваги включається матриця теплопоглинання (демпфування) С:

Матриця демпфування залежить від добутку коефіцієнту демпфування С на щільність матеріалу RO (і помножених на товщину елементу Н, якщо це пластина).
Типи скінченних елементів
Скінченні елементи теплопровідності
|
№ 1505Стержневий КЕ теплопровідності
|
№ 1508Трикутний КЕ теплопровідності
|
|
№ 1509Чотирикутний КЕ теплопровідності
|
№ 1512КЕ теплопровідності у формі тетраедру
|
|
№ 1514Об'ємний шестивузловий КЕ теплопровідності
|
№ 1516Об'ємний восьмивузловий КЕ теплопровідності
|
Скінченні елементи конвективного теплообміну
|
№ 1551Одновузловий КЕ конвективного теплообміну
|
№ 1555Двовузловий КЕ конвективного теплообміну
|
|
№ 1558Трикутний КЕ конвективного теплообміну
|
№ 1559Чотирикутний КЕ конвективного теплообміну
|
Види навантажень
Стаціонарні види навантажень
1. Постійна температура у вузлі (або гранична умова першого роду)
Коли задана температура одного із вузлів:
 , °С
, °С
Аналогом у міцністній задачі є задане переміщення вузла.
2. Тепловий потік (або гранична умова другого роду)
Коли зовнішнє навантаження P дорівнює:

За визначенням тепловий потік – це кількість теплоти, що проходить через ізотермічну поверхню (умовну поверхню з однаковою температурою) за одиницю часу.
Вимірюється в Дж/c*м2 (або Вт/м2, оскільки 1  = 1 Дж/c).
= 1 Дж/c).
В ЛІРІ-САПР є можливість задавати тепловий потік на вузол, пластину чи об'ємне тіло.
2.1. Тепловий потік на вузол
При заданні теплового потоку на вузол необхідно обчислити площу, через яку проходить потік (у разі розгляду балки, це буде площа перерізу). Наприклад, якщо величина теплового потоку q = 100 Дж/c*м2, а площа через яку проходить потік дорівнює 0,1 м2, тто величина навантаження, що задається на вузол Р, дорівнює 100*0,1 = 10 Дж/c .
|
|
|
2.2. Тепловий потік на ребро пластини
При заданні теплового потоку на ребро необхідно чисту величину теплового потоку множити на товщину пластини. Наприклад, якщо величина теплового потоку q = 100 Дж/c*м2, а товщина пластини дорівнює 0,1 м, то величина навантаження, що задається на вузол Р, дорівнює 100*0,1 = 10 Дж/c*м.

2.3. Тепловий потік на об'ємне тіло
У випадку завдання теплового потоку на грань об'ємного тіла: не потрібно множити, ні на площу, ні на довжин. Необхідно лише вказати номер грані, на яку діє потік та величину самого потоку q = 100 Дж/c*м2.
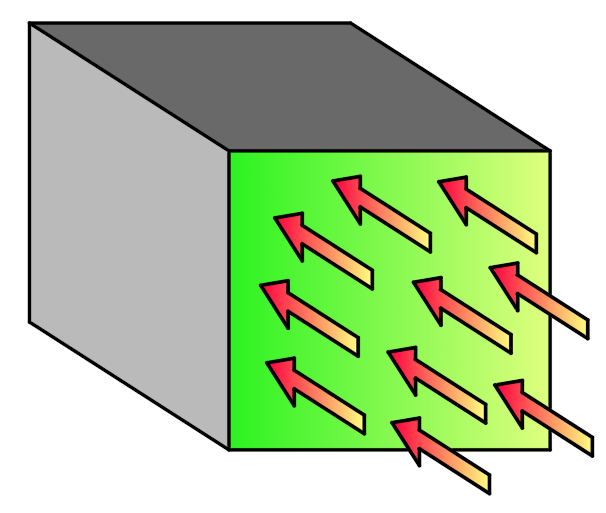
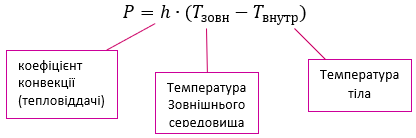
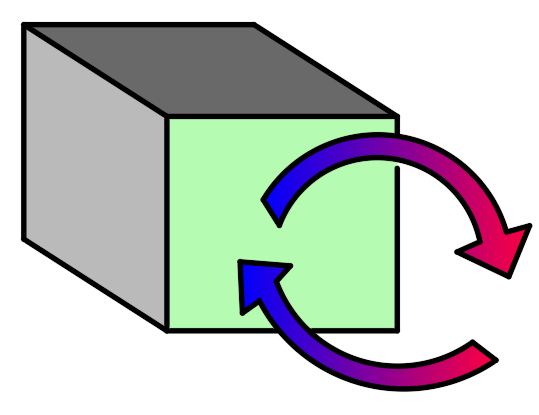
3. Конвективний теплообмін (або гранична умова третього роду)
Коли зовнішнє навантаження P дорівнює:
Конвективний теплообмін – це процес втрати тепла тілом за рахунок того, що при русі повітря відбувається зіткнення окремих частинок, у яких різна температура. При конвективному теплообміні відбувається тепловіддача між поверхнею тіла і середовищем, що рухається (наприклад, повітрям).
Створення конвективного навантаження на схему відбувається у 2 етапи:
На першому етапі потрібно створити скінченний елемент конвекції у місці контакту схеми з повітрям.
- Для стержня – контакт моделюється через одновузловий КЕ конвекції (КЕ №1551).
- Для пластини – контакт моделюється через двовузловий КЕ конвекції (КЕ №1555).
- Для об'ємного тіла – через пластинчасті КЕ конвекції (КЕ №1558 і №1559).
У жорсткості такого скінченного елементу потрібно вказати коефіцієнт конвективної тепловіддачі та площу контакту (для одновузлового КЕ) або висоту контактної поверхні (для 2-вузлового КЕ). Коефіцієнт конвективної тепловіддачі h вимірюється в Дж/c*м2*оС.
На другому етапі потрібно прикласти навантаження на контактний елемент. Через завдання навантаження формується зовнішня температура повітря.
Приклад завдання конвективного навантаження дивіться в «Прикладі рішення стаціонарної задачі теплопровідності» и «Прикладі вирішення динамічної теплопровідності для задачі вогнестійкості».
Нестаціонарні види навантажень
З усіх видів нестаціонарних навантажень: безпосередньо на вузол (елемент) можна задати лише тепловий потік, що змінюється в часі на вузол. Всі інші види нестаціонарних навантажень можна задати, лише використовуючи діалогове вікно «Формування динамічних завантажень із статичних».
Змінюваний у часі Тепловий потік
1.1. На вузол
Є три види навантаження на вузол, що змінюється в часі (аналогічно міцністній задачі):
- ламана з довільним кроком
- синусоїдальна;
- ламана з рівномірним кроком.
Величина навантаження визначається аналогічно стаціонарному тепловому потоку, тобто значення чистого теплового потоку множиться на площу, через яку проходить цей потік.
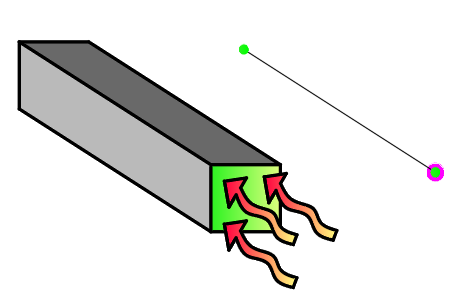
1.2. На ребро пластини чи на грань об'ємного КЕ
Щоб задати нестаціонарний тепловий потік на ребро пластини або на грань об'ємного КЕ потрібно задати стаціонарний тепловий потік у будь-якому Завантаженні, крім Завантаження 4. Оскільки, Завантаження 4 призначене для завдання демпфуючих навантажень.
Після цього у вікні «Динаміка в часі зі статичних завантажень» потрібно сформувати Нестаціонарне завантаження з відповідного стаціонарного, шляхом задання закону зміни навантаження у часі.
Для формування теплового потоку можна використати наступні закони перетворення:
- ламаний з довільним кроком (1);
- синусоїдальний (2);
- ламаний з рівномірним кроком (4).
2. Змінюваний у часі Конвективний теплообмін
Використовувати такий тип навантаження можна, якщо температура середовища, що рухається (наприклад, повітря) може значно змінюватися в часі.
Як було сказано вище, завдання нестаціонарного конвективного теплообміну відбувається так само, як і завдання теплового потоку на ребро або на грань (тобто через формування динамічних навантажень зі статичних).
3. Змінюваний у часі Променистий теплообмін
(або радіаційний теплообмін)
Коли зовнішнє навантаження P дорівнює:
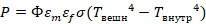
Ф – кутовий коефіцієнт
εm – коефіцієнт поглинання (ступінь чорноти поверхні конструкції)
εf – коефіцієнт випромінювання (ступінь випромінювання джерела)
σ – постійна Стефана Больцмана (рівна 5,67*10-8Вт/м2К4)
Променистий теплообмін відбувається за рахунок того, що частина теплової (внутрішньої) енергії тіла (яка існує завдяки механічному коливанню елементарних частинок, з яких складається тіло) перетворюється на енергію випромінювання. Енергія випромінювання - це енергія електромагнітних коливань із хвилями різної довжини. Виникають електромагнітні хвилі за рахунок коливання заряджених частинок (електронів або іонів), що входять до складу тіла. При попаданні променистої енергії на якесь тіло, частина цієї енергії поглинається, частина – проходить крізь тіло, а частина – відбивається. Ступінь поглинання тілом променевої енергії враховується через коефіцієнт εm. Наприклад, для бетону цей коефіцієнт дорівнює 0,75, а для абсолютно чорного Тіла – 1.
Кутовий коефіцієнт Ф зазвичай приймається рівним 1, він враховує розташування джерела випромінювання по відношенню до поглинача.
Приклад завдання променистого навантаження дивіться в «Приклад вирішення динамічної теплопровідності для задачі вогнестійкості».
Можна підбити підсумки
Тепло - це енергія, що виникає за рахунок руху частинок, з яких складається тіло (атомів або молекул). Усього існує три основні види передачі тепла: теплопровідність, конвекція та променистий теплообмін.
1. Теплопровідність – коли тіло проводить тепло шляхом хаотичного руху частинок, від більш нагрітої частини тіла до менш нагрітої.

2. Конвекція – вид теплообміну, який відбувається за рахунок руху текучого середовища (рідини або газу) в оточенні тіла.

3. Променистий теплообмін – коли тепло передається через електромагнітні хвилі.

Приклад вирішення стаціонарного задачі теплопровідності
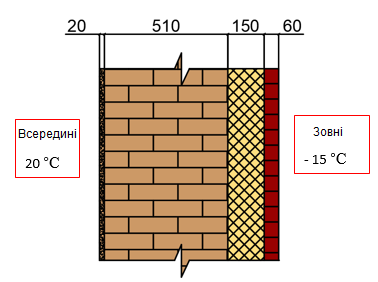
Розглянемо приклад розрахунку теплопровідності зовнішньої стіни цегляного будинку.
Створюємо задачу в 15-й ознаці схеми, яка існує спеціально для вирішення задач теплопровідності. Розглянемо ділянку стіни довжиною 1 метр.
КРОК 1. ГЕОМЕТРІЯ
КРОК 2. Створення елементів КОНВЕКЦІЇ
Щоб задати температуру повітря, додаємо стержневі елементи на внутрішній та зовнішній поверхні стіни, та міняємо їх тип на КЕ №1555.
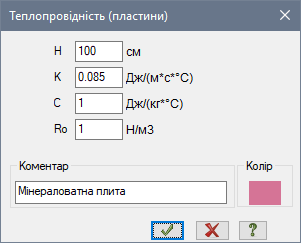
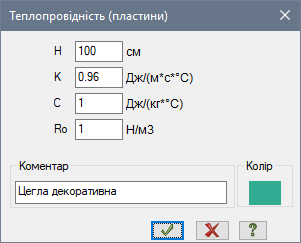
КРОК 3. ХАРАКТЕРИСТИКИ МАТЕРИАЛІВ
Задамо відповідні коефіцієнти теплопровідності K для шарів стіни. Значення коефіцієнта теплопоглинання C та питомої ваги R0 у статичному розрахунку не враховуються, тому їх можна задати рівними одиницям.
Для елементів конвекції теж створюємо жорсткість, і задаємо там коефіцієнти конвекції внутрішнього та зовнішнього шару:
КРОК 4. ЗОВНІШНЄ НАВАНТАЖЕННЯ
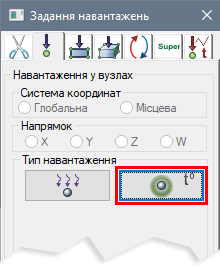
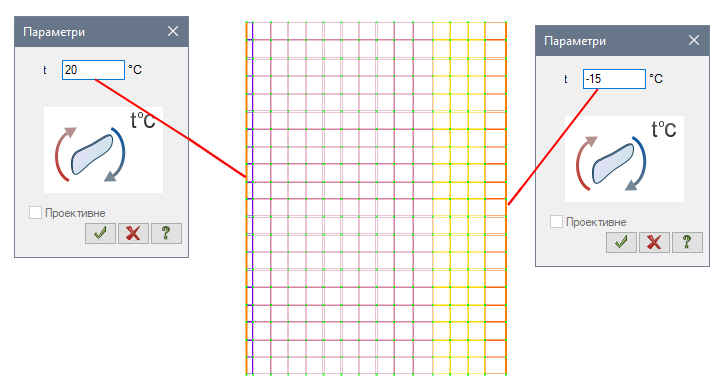
Через зовнішнє навантаження ми задаємо температуру повітря для елементів конвекції. Для цього, у розділі Навантаження відкриваємо конвективний теплообмін  і задаємо температуру всередині та зовні стіни.
і задаємо температуру всередині та зовні стіни.
КРОК 5. ПЕРЕГЛЯД РЕЗУЛЬТАТІВ
Приклад розв'язання динамічної теплопровідності для задачі вогнестійкості
Вирішення задачі теплопровідності є важливим етапом при визначенні вогнестійкості конструкції.
В Eurocode EN 1992-1-2 (2004) (пункт 4.3.1 (3)) написано «Advanced calculation methods should include calculation models for the determination of: the development and distribution of the temperature within structural members (thermal response model)…» ;
У СТО 36554501-006-2006 «Правила із забезпечення вогнестійкості та вогнезбережності залізобетонних конструкцій» (пункт 4.13) сказано: «Розрахунок вогнестійкості та вогнезбереження рекомендується проводити по наведеному перерізу, коли переріз елементу розбивається на малі характерні ділянки, нагріті до різних температур, і кожна мала ділянка приводиться до ненагрітого бетону з урахуванням відповідних знижувальних характеристик міцності бетону.», і у пункті 5.3. додано: «Температуру бетону визначають теплотехнічним розрахунком …».
В ДТСУ-Н EN 1991-1-1:2010 (пункт 4.3.1) сказано: «Уточнені методи розрахунку включають розрахункові моделі для визначення наступного: зростання та розподілення температури по всіх елементах конструкції (теплотехнічний розрахунок);…».
Тому можна сміливо сказати, що без теплопровідності нікуди ☺
Розглянемо тепер приклад того, як визначити розповсюдження тепла від пожежі по перерізу балки, розмірами 160х320 мм. Оскільки наша балка не змінного перерізу, то можна розглядати пласку задачу, де ширина всіх елементів дорівнюватиме одному погонному метру балки (100 см).
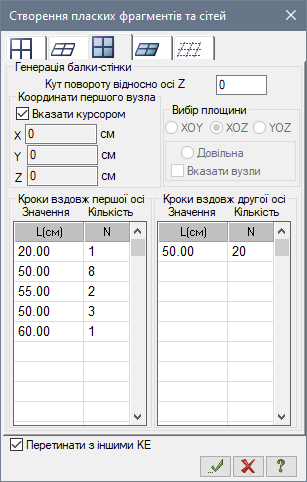
КРОК 1. ГЕОМЕТРІЯ
Створюємо схему перерізу балки в 15-й ознаці схеми (рис. 17).
|
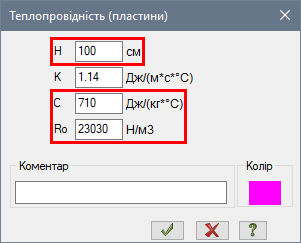
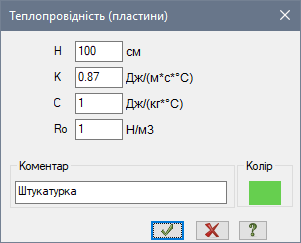
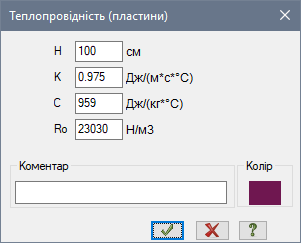
Призначимо жорсткість для елементів теплопровідності:
Рис. 16. Властивості теплопровідності
|
Рис. 17. КЕ модель
|
В СТО 36554501-006-2006 «Правила із забезпечення вогнестійкості та вогнезбережності залізобетонних конструкцій» (пункт 6.3) для теплотехнічного розрахунку рекомендують приймати теплопровідність та теплоємність бетону по формулах (розглянемо приклад важкого бетону на карбонатному заповнювачі):
- теплопровідність: λ=1,14-0,00055t, [Дж/c*м*оС.]
- коефіцієнт теплоємності: C=0,71+0,00083t, [кДж/кг*оС.]
де  – це температура,
– це температура,  .
.
Оскільки теплопровідність та теплоємність залежать від температури, то для нашого завдання ми використовуємо властивості бетону, що розраховані для температури 300 °С. Саме з такими характеристиками бетону виходять максимально схожі результати температурних кривих прогріву перерізу з тими, що наведені в нормах.
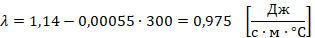

КРОК 2. Зовнішнє навантаження. ПЕРЕДІСТОРІЯ
Після цього починаємо задавати граничні умови (зовнішнє навантаження). В Завантаження 1 виділяємо всі вузли схеми, і задаємо їм постійну температуру, яка дорівнює 20 °С. Це стандартне значення для передісторії, оскільки вважається, що середня температура конструкції на початок пожежі є саме такою. Після цього всі вузли забарвлюються у зелений колір, рис.17.
КРОК 3. Зовнішнє навантаження. КОНВЕКЦІЯ
Як було вже сказано, існує три основні види передачі тепла. Саму теплопровідність усередині тіла ми вже врахували шляхом задання жорсткості. Залишається конвекція та променистий теплообмін.
Тому, для формування конвективного теплообміну, ми створимо контактні двовузлові скінченні елементи з тих боків балки, які імовірно будуть піддані впливу вогню: зліва, знизу та праворуч (рис. 19, б). Створюємо «жорсткість» для елементів конвекції, і задаємо там товщину нашого перерізу Н = 100см, а також коефіцієнт конвекції а=25 Дж/(м2*с*°С). Коефіцієнт конвекції, що дорівнює 25 – це нормативна величина для стандартного графіка розвитку пожежі.
|
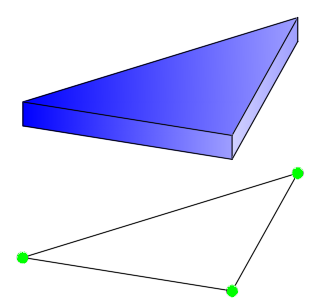
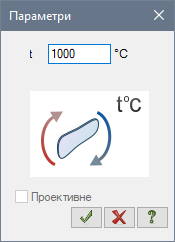
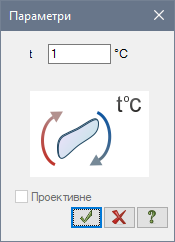
Після цього необхідно сформувати зовнішню температуру середовища. Для цього використовуємо вид навантаження під назвою задана температура t:
Навантаження на конвективні елементи формуємо у Завантаженні 5, при цьому Завантаження 2-4 залишаємо вільними. У вікні задання температури (рис. 18) записуємо одиницю. Трохи пізніше, на стадії формування Динамічного навантаження із статичного, ми будемо задавати графік зміни температури під час пожежі. Величини температур з цього графіку будуть автоматично множитимуться на число, яке ми введемо в цьому вікні. Оскільки числа з графіку нам змінювати не потрібно, то у вікні заданої температури ми просто записуємо одиницю. |
Рис. 18. Навантаження на елементи конвекції
|
Після задання конвективного навантаження контактні елементи забарвлюються в помаранчевий колір (рис. 19, в).
КРОК 4. Зовнішнє навантаження. ПРОМЕНИСТИЙ ТЕПЛООБМІН (або РАДІАЦІЯ)
Як було сказано раніше, теплове випромінювання – це вид теплообміну, який здійснюється шляхом поглинання електромагнітних хвиль. Якщо у разі конвективного навантаження, площу контакту з поверхнею ми задаємо через жорсткість конвективного елементу (ми задавали Н=100 см), то у випадку променистого теплообміну, площу контактної поверхні потрібно задавати через навантаження виду Тепловий потік на вузол або на ребро пластини, (у випадку об'ємного скінченного елементу тепловий потік потрібно задавати на грань елементу). При розрахунку, на кожному кроці інтегрування, це число множитиметься на добуток: Ф*εm*εf*σ*(Твнеш4-
Твнутр4), де  - температура з графіку пожежі, що буде задаватися на наступному кроці, а
- температура з графіку пожежі, що буде задаватися на наступному кроці, а  - температура у вузлі розрахункової схеми.
- температура у вузлі розрахункової схеми.
Відразу постає питання, навіщо площа задавати через навантаження? І він справедливий ☺
Постараємося знайти на нього відповідь. Для цього, розглянемо окремо два варіанти формування променистого теплообміну.
Варіант 1 (якщо задавати потік тепла на вузол)
Тепловий потік на вузол визначається як чистий тепловий потік Дж/c*м2, помножений на площу, через яку проходить цей потік [м2]. У випадку радіації ми приймаємо, що чистий тепловий потік =1. Нам потрібно лише знайти площу поглинання, яка приходить на кожен вузол схеми.
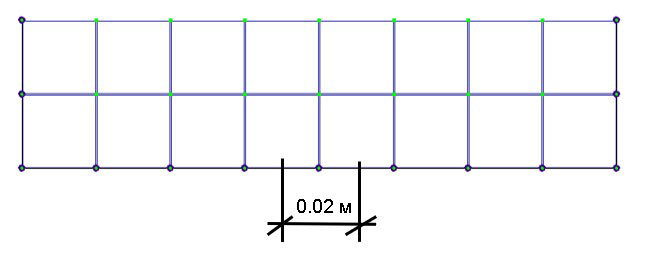
Якщо ми розглянемо частину розрахункової схеми (рис. 20), де розміри кожного КЕ дорівнюють 20х20 мм, а товщина = 1 м, то контактна поверхня, яка припадає на 1 вузол дорівнює:
(0,01м +0,01м)*1м =0,02 м2.
Значить, у Завантаженні 6, на кожен контактний вузол задаємо тепловий потік, який дорівнює 0,02 м2∙1[Дж/c*м2]= 0,02 [Дж/c], і отримуємо схему, яка зображена на рис.19, г.
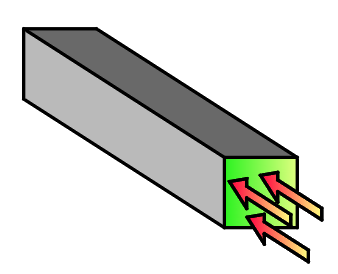
Варіант 2 (якщо задавати потік тепла на ребро пластини)
Як і в попередньому варіанті, тепловий потік на ребро визначається як величина чистого теплового потоку Дж/c*м2, помножена, в даному випадку, не на площу, а на товщину пластини Н, [м]. На довжину цього ж ребра навантаження множиться автоматично при розрахунку (аналогічно навантаженню на ребро пластини у міцністній задачі).
|
Щоб задати навантаження тільки на певні грані скінченних елементів, потрібно виділити всі вузли цих граней, а також виділити скінченні елементи, яким належать ці грані. При заданні Навантаження на пластини (рис. 21) поставте галочку для автоматичного вибору граней, на які задається навантаження.
Таким чином, для нашої схеми, у Завантаженні 6, на всі контактні грані потрібно задати тепловий потік, який дорівнює:
1
|
Рис. 21. Вибір завантажених граней
|
КРОК 5. ЗАДАННЯ ПОЖЕЖІ. Формування динамічного завантаження
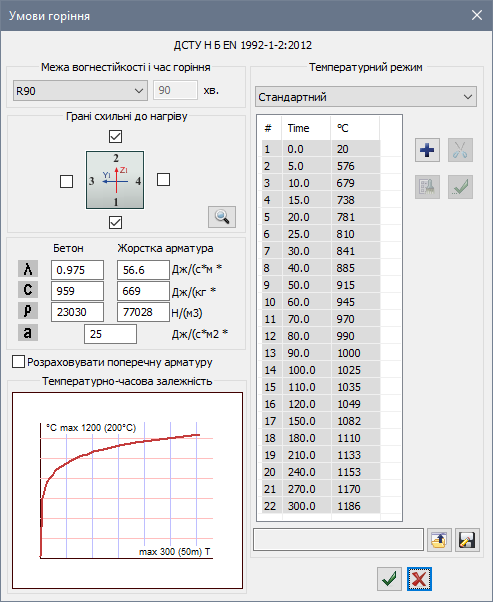
Для задання вогневого впливу використовуємо стандартний графік розвитку пожежі, який визначається по формулі:

τ – час нагрівання в секундах,
te – початкова температура (передісторія) = 20 °С.
Або можна скористатися таблицею 6.1. з СТО:

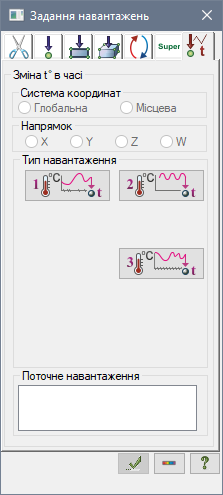
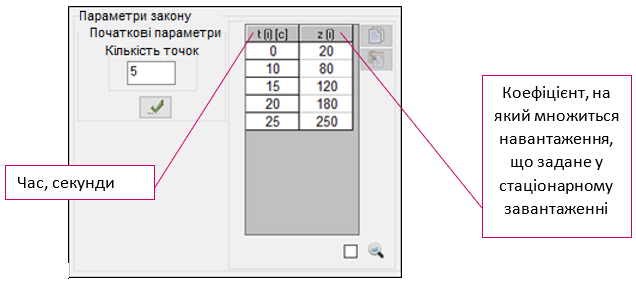
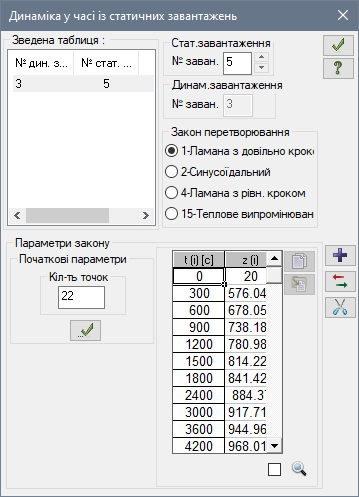
Натискаємо на кнопку Формування динамічних завантажень із статичних, та задаємо зміну конвекції у часі, яка залежить від температури вогню. Формуємо динаміку з 5-го Завантаження (конвекції), (рис.22, а). Задаємо там 21 точку з таблиці 6.1 плюс одна точка на момент часу 0 сек, значення температури в якому, робимо таким же як у передісторії – 20 °С. Час задаємо в секундах (ліва колонка), температуру – у градусах (права колонка).
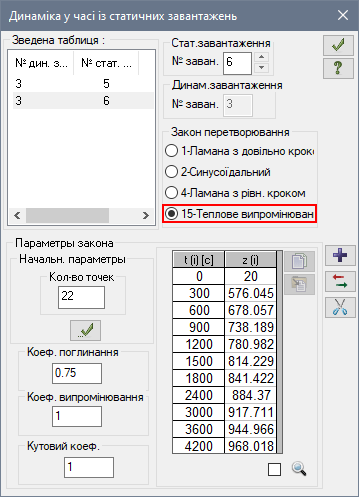
Після цього, аналогічно формуємо радіацію, яка також залежить від температури вогню (рис.22, б). Тільки тепер, формуємо динаміку з Завантаження 6 (радіації), і використовуємо Закон перетворення №15 – Теплове випромінювання. І задаємо коефіцієнт поглинання = 0.75 (для бетону), випромінювання = 1 (для вогню), та кутовий = 1, оскільки вважаємо, що вогонь розташований безпосередньо поблизу балки.
І натискаємо на параметр Виконати розрахунок динаміки у часі:
КРОК 6. ПЕРЕГЛЯД РЕЗУЛЬТАТІВ
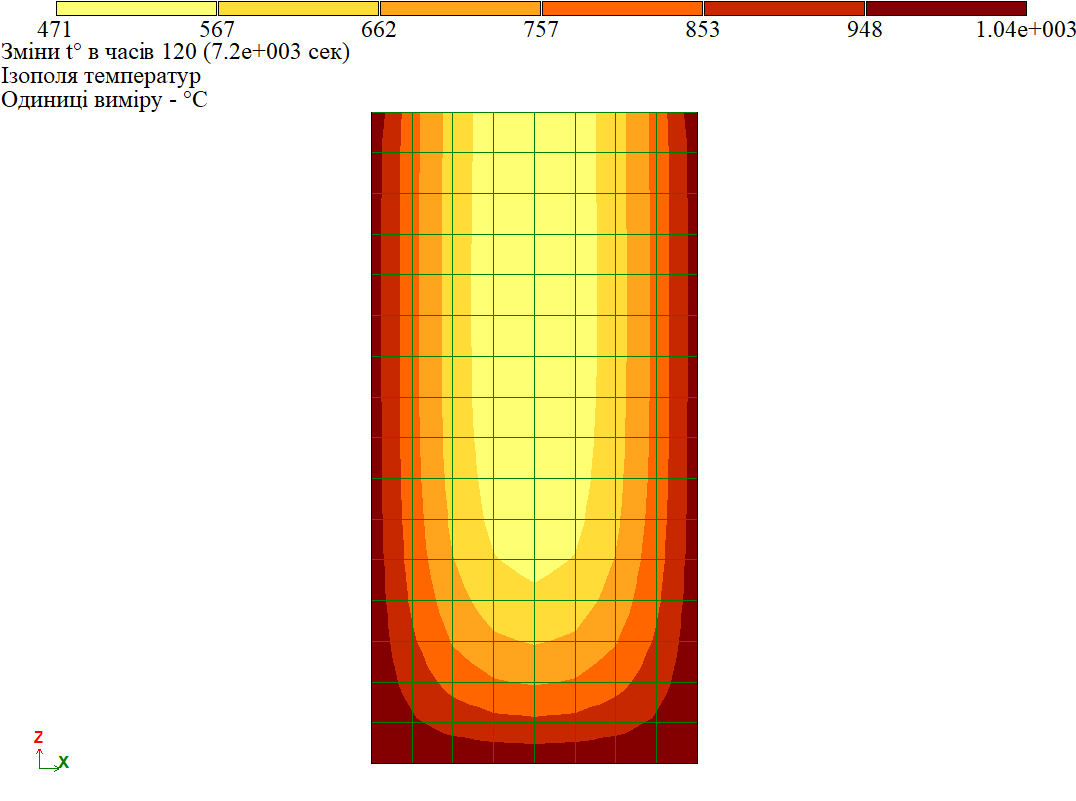
Вище наведено приклад температурних полів по перерізу 7200 секунд (що дорівнює 120 хвилин горіння).
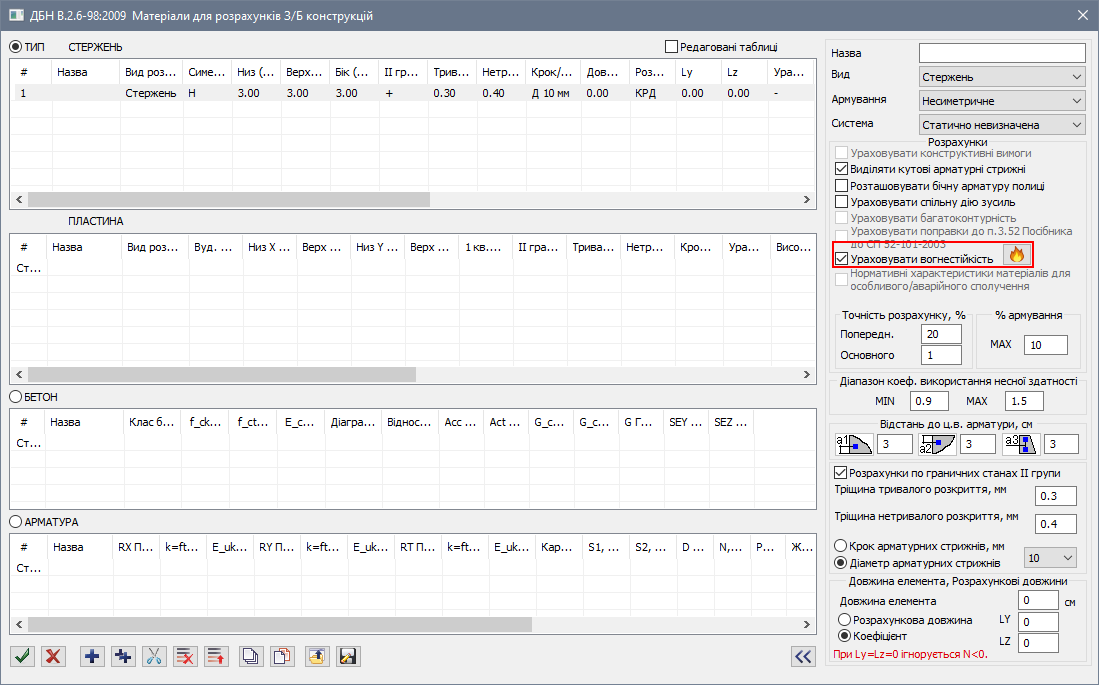
На завершення можна додати, що немає необхідності розраховувати прості перерізи вручну, кожне з них перераховувати в 15-й ознаці та імпортувати у 5-й для міцністного розрахунку. Це можна зробити через вкладку Вогнестійкість у Розрахунковому модулі Залізобетон, при завданні матеріалів. Після формування врахування вогнестійкості в елементі буде підібрана арматура з урахуванням межі вогнестійкості конструкції.
Але завдяки 15-й ознаці схеми, у користувача є можливість розрахувати на вогнестійкість перерізи або просторові задачі будь-якої конфігурації та складності.
Стаття "Розв'язання задачі теплопровідності" у форматі PDF
Приклад "Динамічна теплопровідність"
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.






















 ∙ 1 м = 1
∙ 1 м = 1  .
.



Коментарі