Визначення суми теплових потоків, які перетинають досліджувану область

Тепло мимовільно переноситься лише у бік зменшення температури. Кількість тепла, що переноситься через будь-яку ізотермічну поверхню в одиницю часу, називається тепловим потоком Q [1].

У стаціонарних процесах теплопровідності температура у будь-якій точці твердого тіла залежить від часу, інакше 𝜕𝑡/𝜕𝜏=0.

В умовах стаціонарного теплового стану плоского тіла тепловий потік описується законом Фур'є:

(1)

де Q - const для будь-якої координати х;

𝜕𝑡/𝜕𝜏 – градієнт температури;

F(x) - поверхня тіла, відповідна координаті х;

λ - коефіцієнт пропорційності, званий коефіцієнтом теплопровідності.

Аналогічне рівняння можна записати для циліндричного тіла, замінивши координату x на r.

(2)

Інтенсивність процесу стаціонарної теплопровідності оцінюють за допомогою щільності теплового потоку.

Тепловий потік, віднесений до одиниці площі ізотермічної поверхні, називається щільністю теплового потоку q.

Щільність теплового потоку є вектор, напрямок якого збігається з напрямком розповсюдження тепла в даній точці та протилежно напрямку вектора температурного градієнту (рис. 1) [1].

У разі плоскої стінки, коли внутрішня та зовнішня її поверхні рівні, щільність теплового потоку дорівнює (Вт/м²= Дж/(c·м²)):

(3)

У разі циліндричної стінки її поверхня в міру віддалення від осі збільшується, а щільність теплового потоку зменшується. Тому для оцінки інтенсивності теплопровідності через циліндричну стінку використовують поняття щільності теплового потоку на погонний метр (Вт/м= Дж/(c·м)):

(4)

де, 1 - довжина, r - радіус циліндричної стінки, м.

Тест 2 Стаціонарне розповсюдження тепла в пластині (переріз кільце) за граничних умов першого роду (задана температура)

Тест 3 Стаціонарне розповсюдження тепла в пластині (переріз кільце) при змішаних граничних умовах першого та третього роду (задана температура та конвекція)

При стаціонарному тепловому стані плоскої стінки тепловий потік через неї постійний. Тому, проінтегрувавши рівняння (3), прийнявши при цьому λ = const, отримаємо для одношарової стінки такий вираз (Вт/м²= Дж/(c·м²)):

(5)

де t₁ и t₂ - температура відповідно на внутрішній та зовнішній поверхнях стінки, ⁰С;

S - товщина стінки, м.

Тест 7 Стаціонарне поширення тепла в стержні за граничних умов третього роду (конвекція)

Якщо плоска стінка має n шарів, то щільність теплового потоку через неї можна виразити наступним чином (Вт/м²= Дж/(c·м²)):

(6)

У цьому випадку кожен шар має свої товщину S_i та коефіцієнт теплопровідності λ_i. Відношення S/λ називають термічним опором шару.

Тест 8 Стаціонарне поширення тепла в неоднорідному стержні за граничних умов третього роду (конвекція)

Тест 11 Стаціонарне поширення тепла по радіусу порожньої кулі за граничних умов третього роду (конвекція)

Тест 12 Стаціонарне поширення тепла по радіусу неоднорідної порожньої кулі за граничних умов третього роду (конвекція)

Для визначення теплового потоку, що проходить через стінку при стаціонарному тепловому стані, необхідно його щільність q помножити на поверхню плоскої стінки, тобто:

(7)

Приклад розрахунку

Визначити тепловий потік Q (Дж/c), що проходить через плоску двошарову стінку, яка має поверхню F = 12 м², а також знайти температуру на межі шарів, якщо відомо, що стінка складається з шару шамоту товщиною S₁ = 0,46 м і шару теплоізоляції товщиною S₂ = 0,25 м; коефіцієнти теплопровідності шарів відповідно λ₁ = 0,84 Дж/(м*с*°С) и λ₂ = 0,28 Дж/(м*с*°С); температура внутрішньої поверхні стінки t₁ = 1395°С, температура зовнішньої поверхні t₃ = 80°С.

Рішення

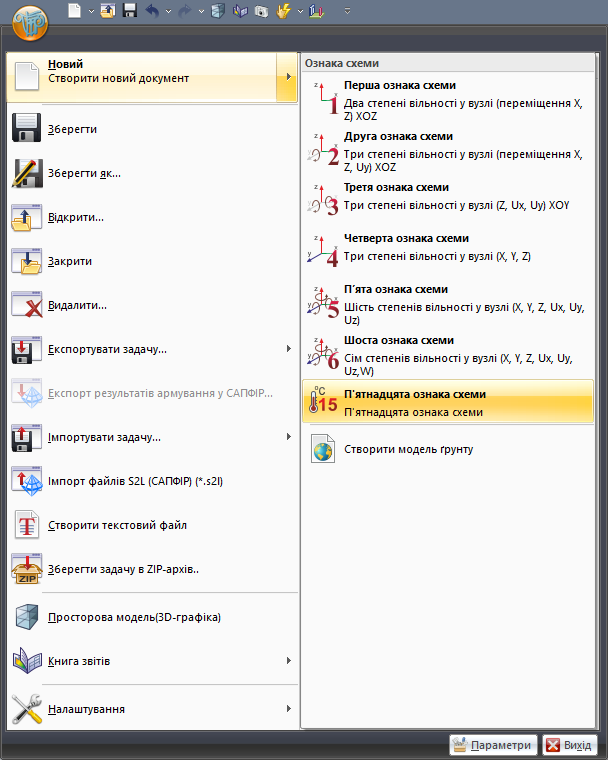
Створюємо задачу в 15-й ознаці схеми - задачі теплопровідності (одна ступінь свободи у вузлі – температура t) (рис. 2).

Розглянемо ділянку стіни висотою 1 метр. Товщина першого шару S₁ = 0,46 м (шар шамоту), товщина другого шару S₂ = 0,25 м (теплоізоляція).

КРОК 1. Геометрія

Задамо балку-стінку за допомогою команди Створення плоских фрагментів та сітей (рис.3).

У п'ятнадцятій ознаці схеми для 4-х вузлових пластин за умовчанням призначається тип КЕ 1509 – чотирикутний скінченний елемент теплопровідності.

КРОК 2. Характеристики матеріалів

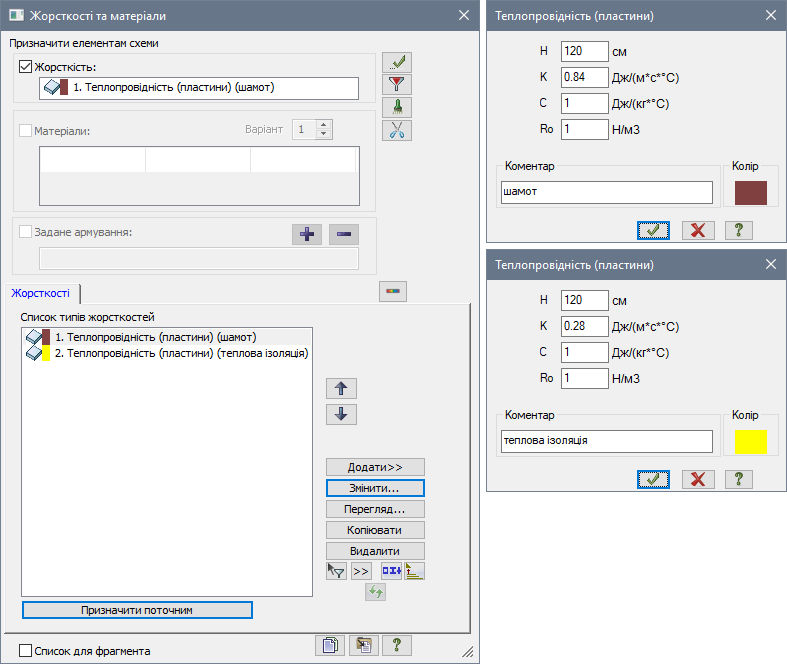
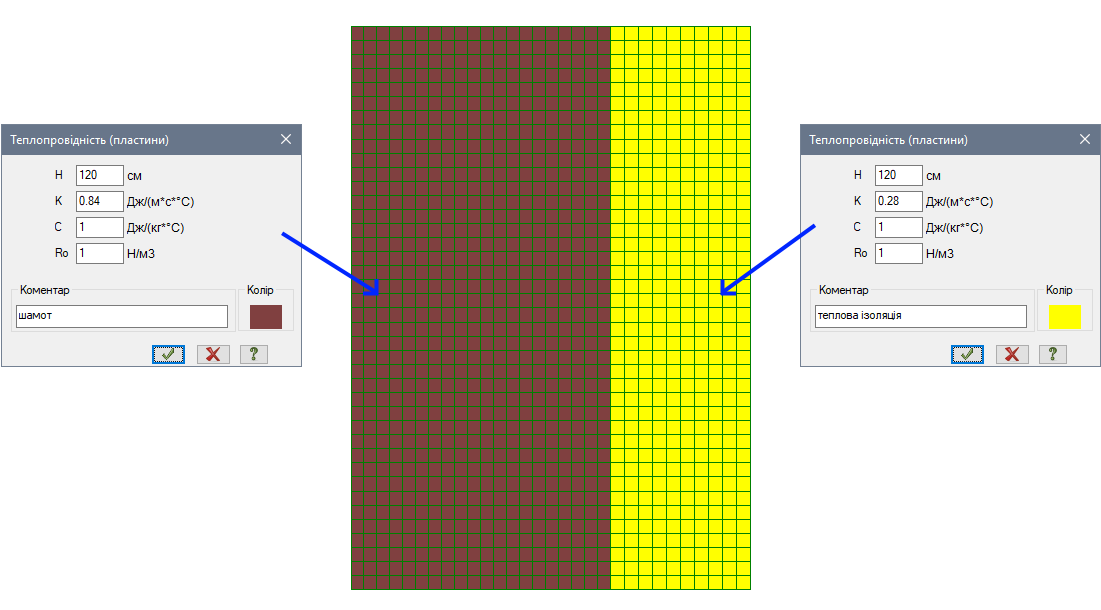
За допомогою діалогового вікна Жорсткості та матеріали (рис. 5) створимо набір жорсткостей Теплопровідність (пластини), де задамо відповідні коефіцієнти теплопровідності K для шарів стіни. Значення коефіцієнта теплопоглинання C та питомої ваги R_o у задачах стаціонарної теплопровідності не враховуються, тому їх можна задати рівними одиниці.

Призначимо жорсткість на елементи розрахункової схеми (рис.6).

КРОК 3. Зовнішнє навантаження

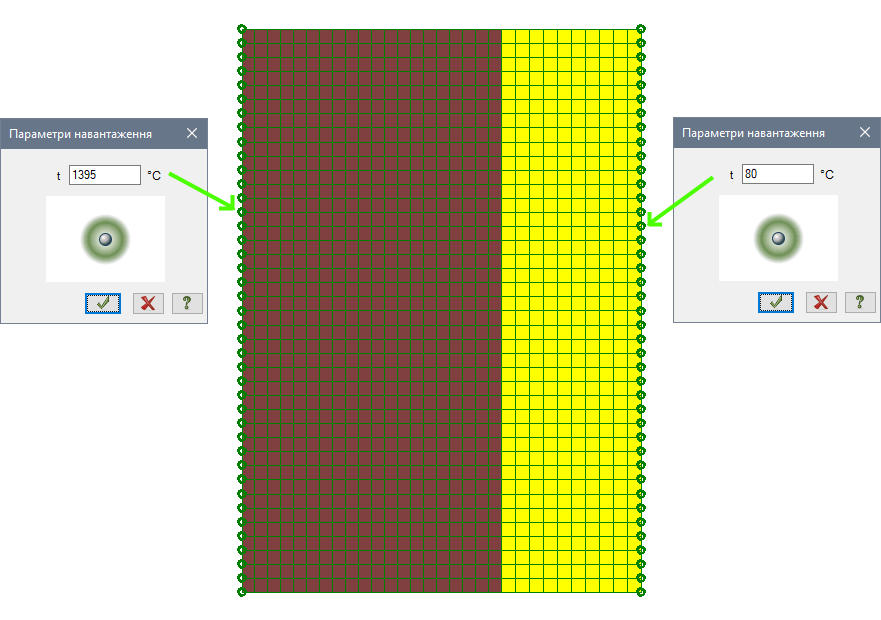
Температуру внутрішньої та зовнішньої поверхні стінки задаємо як задану температуру у вузлах. У діалоговому вікні Завдання навантажень вибираємо закладку Навантаження у вузлах → Задана температура , в у діалоговому вікні Параметри задаємо температуру:

- температура внутрішньої поверхні стінки t₁ = 1395°С;

- температура зовнішньої поверхні t₃ = 80°С(рис.7).

КРОК 4. Тепловий потік у вузлах

Щільність теплового потоку через двошарову стінку можна визначити за формулою (6):

(8)

Тепловий потік по формулі (7):

(9)

В ПК ЛІРА-САПР у процесі розрахунку визначається тепловий потік у вузлах розрахункової схеми від обраних елементів. Для цього у діалоговому вікні Розрахувати тепловий потік (рис.8) необхідно задати наступну інформацію:

– номери вузлів, в яких повинен бути обчислений тепловий потік;

– номери елементів, які передають тепловий потік у ці вузли.

Списки елементів та вузлів можна редагувати вручну, перерахувавши у відповідних полях їх номери. Якщо на схемі попередньо виділити елементи та вузли, то скласти списки для розрахунку теплового потоку у вузлах можна автоматично за допомогою кнопок Оновити. У відповідних полях Список елементів і Список вузлів відобразяться переліки номерів лише тих елементів/вузлів, які на момент натискання кнопки відмічені на схемі.

КРОК 5. Перегляд результатів

Виконуємо розрахунок схеми. Стає доступним перегляд результатів у вигляді Мозаїк теплового потоку (рис. 9).

Для визначення теплового потоку, що проходить через стінку при стаціонарному тепловому стані, необхідно виконати підсумовування теплового потоку у вузлах. Для цього виділяємо вузли, в яких було раніше обчислено тепловий потік і в діалоговому вікні Підсумовування навантажень натискаємо кнопку Застосувати (рис.10).

Знайдемо температуру границі шарів, пам'ятаючи, що тепловий потік через кожний шар є величина постійна, тобто:

(10)

З наведеного вище виразу випливає, що:

(11)

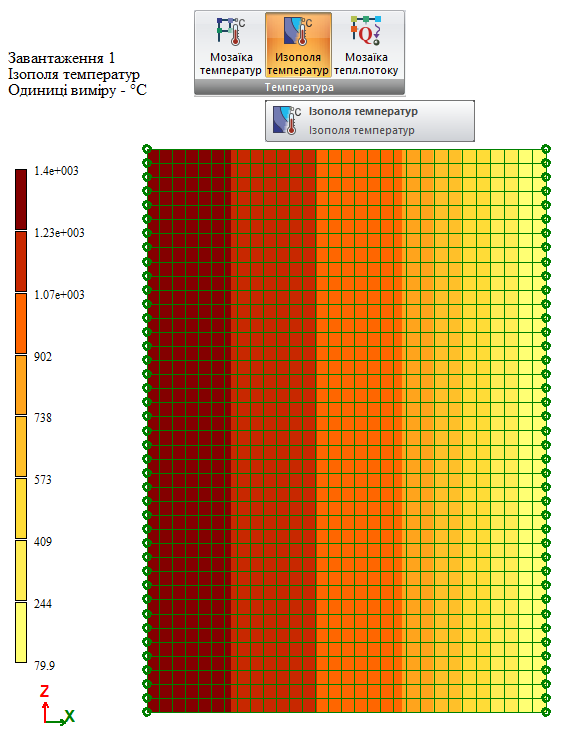
У ПК ЛІРА-САПР після розрахунку стає доступним перегляд результатів у виді Ізополів температур (рис.11).

Список літератури

1. Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е стереотип. «Энергия», 1977 – 344с.
2. Тепловая защита зданий. Актуализированная редакция СНиП 23-02-2003 (с Изменением N 1):СП 50.13330.2012. – [Введен в действие с 07-01-2013 ]. – M.: Минрегион России, 2012. – 100 с. – (Свод правил). (Приложение Н.)
3. Проектирование тепловой защиты зданий:СП 23-101-2004. – [Введен в действие с 01-06-2004 ]. – M., 2004. – 145 с. – (Свод правил). (Приложение М.)