Шостий ступінь вільності у КЕ оболонка

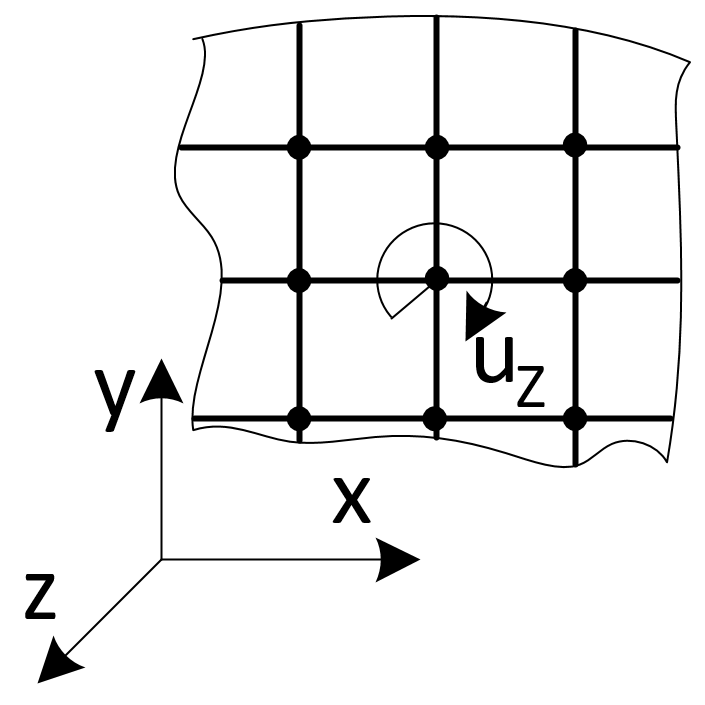
Розрахунки просторових стержневих систем, як правило, передбачають, що в кожному вузлі є шість переміщень (у дусі скінченно-елементного підходу – це шість ступенів свободи) і шість відповідних їм зусиль. Кожна ступінь свободи має фізичний сенс – при лінійних переміщеннях у напрямку осей Х, Y, Z і при куті повороту UX, UY, UZ відносно цих осей. При розрахунку пластинчастих систем куту повороту UZ (шоста ступінь свободи) відносно осі ортогональної площини пластини (рис. 1) надання фізичного сенсу пов'язане з деякою абстракцією.

Історія методу скінченних елементів містить приклади різних екзотичних ; і т.д. Проте всі вони рано чи пізно виявляли свою неспроможність. Так, наприклад, ступінь свободи ; та інші вищі похідні від переміщень при зміні орієнтації глобальної системи координат (необхідна процедура для універсальних розрахункових комплексів) породжують інші типи та ступені свободи.

Чотирьохвузловий скінченний елемент з обертальним ступенем свободи

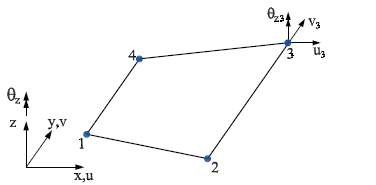
У різних публікаціях дається побудова матриці жорсткості. Так у [4] скінченний елемент виходить шляхом об'єднань апроксимуючих функцій Аллмана (переміщення в площині скінченного елементу) і функцій повороту нормалі (обертальні переміщення) [8] (рис. 2).

Поле обертальних переміщень інтерполюється таким чином:

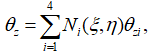
Поле переміщень у площині:

Де

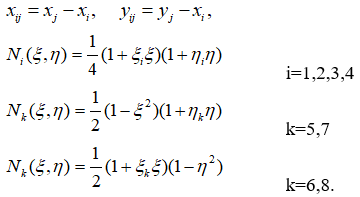
Де k, i, j визначаються як (5,1,2), (6,2,3), (7,3,4), (8,4,1).

Матриці деформацій ε_m визначається як

Де вектор вузлових переміщень.

Матриця похідних B_mi має форму:

Де N_x, N_y, несумісні функції форми визначені як:

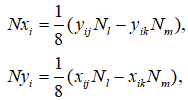
Індекси i, j, k, m приймають значення:

i = 1, 2, 3, 4; m = i + 4; l = m – 1 + 4 floor(1/i);

k = mod (m, 4) + 1; j = l – 4;

матриця деформацій (ε_sk) виражена як

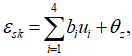
де

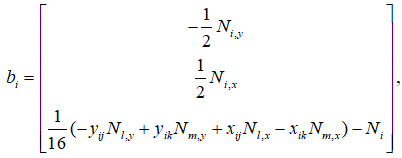
Індекси i, j, k, m визначаються виразом вище.

Варіаційне формулювання методу скінченних елементів, запропоноване [6], визначається як:

Результирующая матрица жесткости является K_mem сумою матриці K_m та штрафної матриці P_γ.

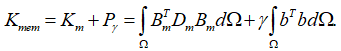
Додатний штрафний коефіцієнт γ у рівнянні є проблемним питанням. Однак прийнято прирівнювати коефіцієнт рівним модулю зсуву (γ=G) [7-8].

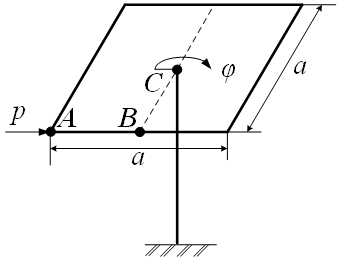
Апологети шостого ступеня свободи як правило наводять горезвісний приклад «парасолька» - задача обпирання плити на одиночну колону при необхідності сприйняття крутних впливів відносно вертикальної осі колони.

Якщо моделювати обпирання пластини на одиночну опору без шостого ступеня свободи у вузлі, то затискання пластини в колоні буде відсутнє, і пластина повертатиметься відносно колони. Розв'яжемо дану задачу з урахуванням шостого ступеня свободи в оболонці.

Приклад 1 – застосування шостого ступеня свободи в конструкціях типу «парасолька»

Вихідні дані: квадратна плита а=6 м, жорстко зчленована з колоною квадратного поперечного перерізу 0,5x0,5 м; довжиною l=6 м, під дією поздовжньої зосередженої сили p= 1 т.

Характеристика матеріалу: Е = 3х10⁶т/м²; ν = 0.2.

Граничні умови: колона біля основи жорстко защемлена. Розрахункова схема показана на рис. 3.

Рішення:

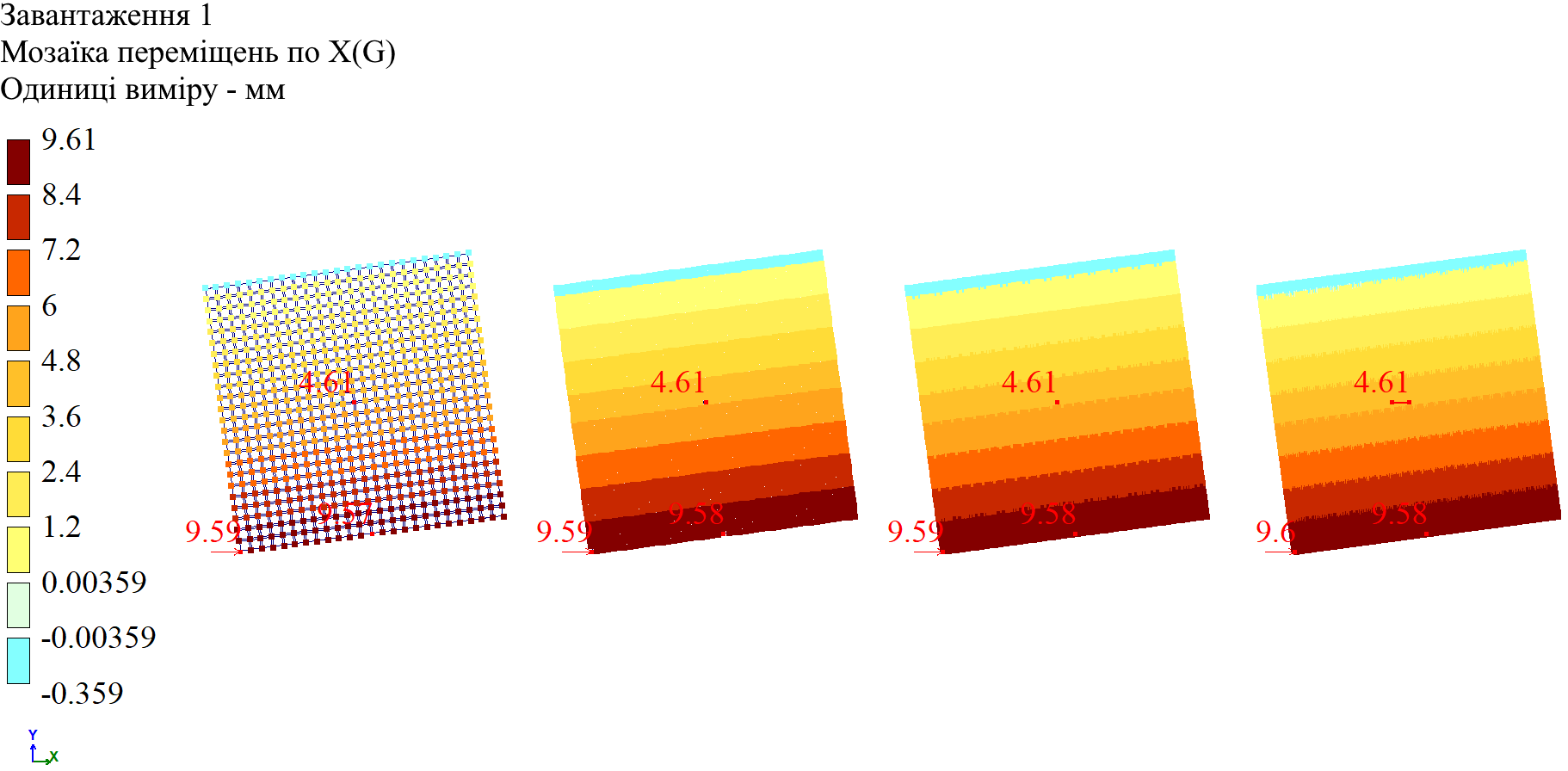
На рис. 4 і у табл. 1 наведено результати розрахунку конструкції типу «парасолька», виконані за допомогою ПК ЛІРА-САПР.

Табл. 1. Результати розрахунку конструкції типу «парасолька»

Аналізуючи результати, наведені в табл.1, можна зробити висновок, що згущення сітки не призводить до уточнення рішення, що свідчить про некоректність застосування шостого ступеня свободи. Подібні проблеми, у трохи іншій площині, розглядаються в [12].

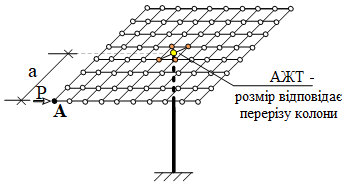
Слід зазначити, що сучасні прийоми моделювання передбачають врахування «тіла» колони. В цьому випадку вузол сполучення колони та пластини розраховується за допомогою абсолютно жорстких тіл (рис. 5,6) і без шостого ступеня можна обійтися. Абсолютно жорстке тіло (АЖТ) – забезпечує кінематичний зв'язок переміщень провідних вузлів та ведучих. У ПК ЛІРА-САПР такого типу жорсткі тіла вводяться в автоматизованому режимі. Жорсткі тіла, що вводяться, можуть моделювати «тіло» колони будь-якої конфігурації (хрестове, кутове, таврове та ін.). Реалізація в ПК ЛІРА-САПР припускає відповідність одному провідному вузлу довільної кількості керованих вузлів.

Такий метод моделювання, з одного боку, вирішує проблему врахування «тіла» колони, тобто «зрізання» піку моментів, що виникає при моделюванні обпирання на колону як на точкову опору. З іншого боку, забезпечує сприйняття колоною крутних деформацій. У більшості випадків, коли є принаймні хоча б дві колони, цього не вимагається, тому що. в цьому випадку крутний момент від деформацій у площині плити сприйматиметься парами поперечних сил у колонах, а крутні моменти будуть зневажливо малі та їх наявність просто можна не враховувати (ефект нехтування моментами в законструйованих жорстких вузлах ферм, коли в розрахунок були введені шарнірні вузли) [1].

Приклад 2 – застосування шостого ступеня свободи у конструкціях типу «складчаста оболонка»

В якості необхідності застосування шостого ступеня свободи наводять моделювання різних просторових пластинчастих систем (рис. 7).

Кожен вузол просторової конструкції такого типу має шість ступенів свободи (три лінійні та три кутові переміщення). Як правило, вузол скінченного елементу плоскої пластини має п'ять ступенів свободи. Це зумовлює появу в канонічній системі лінійно залежних рівнянь, тобто поділ на нуль в процесі виключення невідомих. Використання шостого ступеня свободи, у деяких випадках, вирішує цю проблему. Хоча у просунутих програмних комплексах є процедура, що обходить цю проблему [2]. Якщо у процесі виключення в діагональному канонічному рівнянні з'являється 0, то в цьому напрямку накладається в'язь – у разі відсутності навантаження по цьому напрямку. Ця проста процедура може виявитися корисною і в багатьох інших випадках [2, 10].

І тим не менш у ряді випадків шостий ступінь у руках недосвідчених користувачів може призвести до неправильних результатів.

Приклад 3 – стиковка рамного стержня з діафрагмою

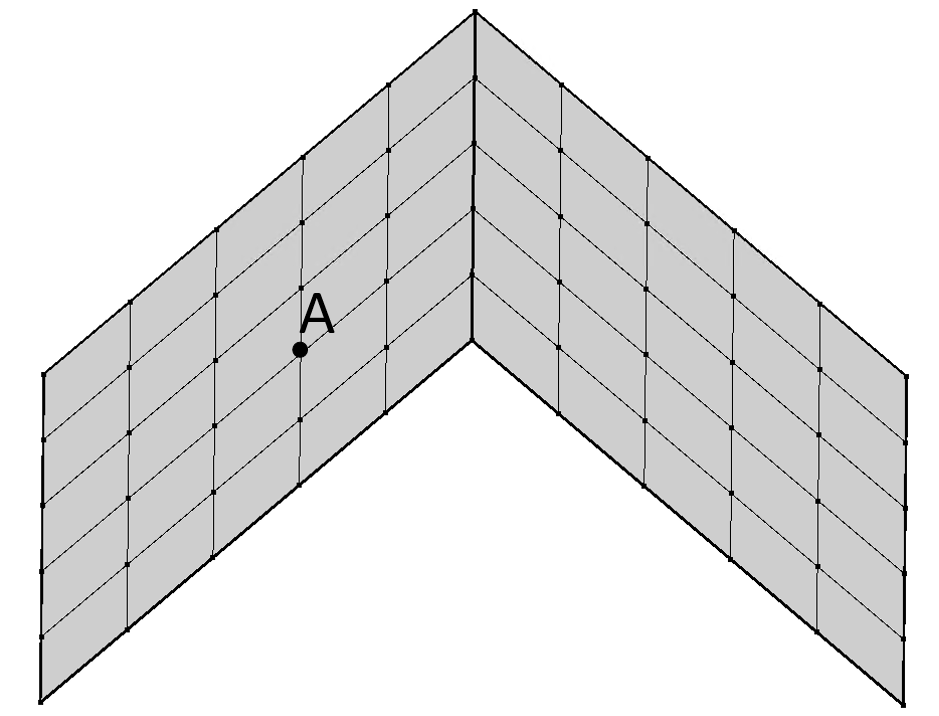
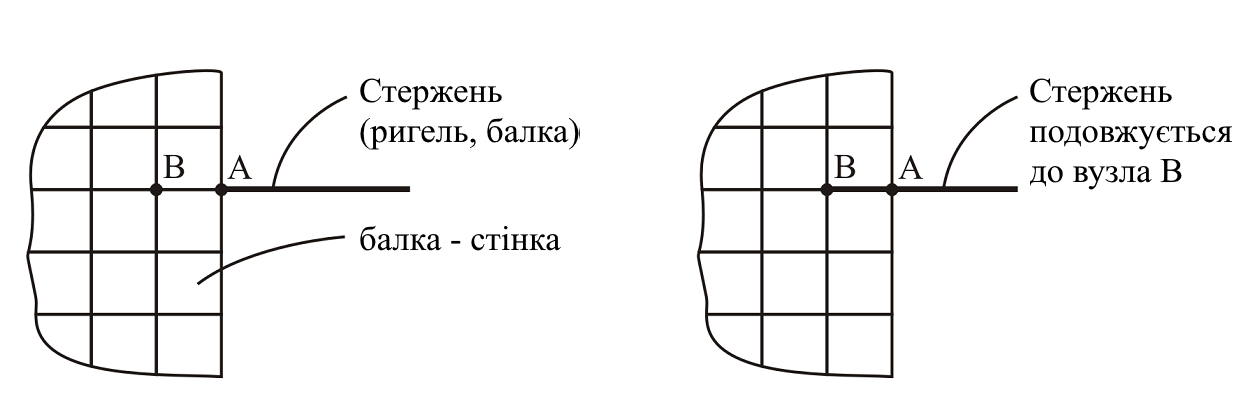
На рис. 8 наведено приклад моделювання защемлення ригеля у стіні. Тут труднощі обумовлені тим, що скінченні елементи плоского напруженого стану (балки-стінки) не мають вузлових невідомих, відповідних куту повороту відносно осі, ортогональної площини діафрагми. Тому вузол у точці А (рис.8) без будь-яких додаткових заходів буде для стержня шарнірним.

Моделювання защемлення за допомогою шостого ступеня свободи призводить до неправильних результатів. При згущенні сітки – момент у защемленні зменшується, тобто результат суттєво залежить від скінченно-елементної сітки, що неправильно.

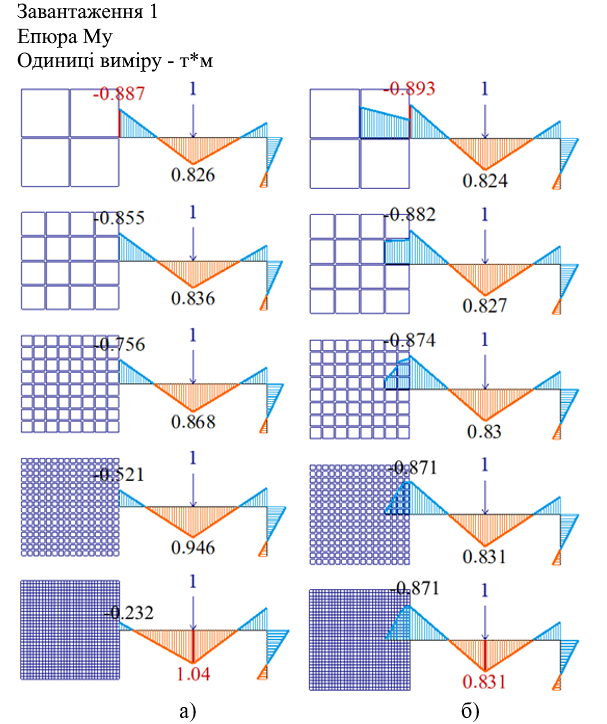
Розглянемо даний приклад. Досліджуємо згинальний момент у балці під дією зосередженої вертикальної сили р=1т при різній густоті сітки. Розрахункова схема показана на рис. 8. Результати розрахунку в ПК ЛІРА-САПР наведено на рис. 9 та в табл. 2.

Табл. 2. Згинальний момент My,т*м при різній густоті сітки

В даному випадку защемлення необхідно моделювати іншими способами (введення АЖТ, заведення ригеля в тіло стіни та ін.) [5]. Для організації защемлення рамного стержня у тілі діафрагми можна рекомендувати введення додаткового стержня між вузлами А та В (рис.9 б, 10). З одного боку, введення такого стержня вноситиме деякі локальні обурення, але, з іншого боку, в ряді випадків це буде моделювати конструктивне рішення вузла (заведення арматури сусіднього стержня з метою анкерування) [1].

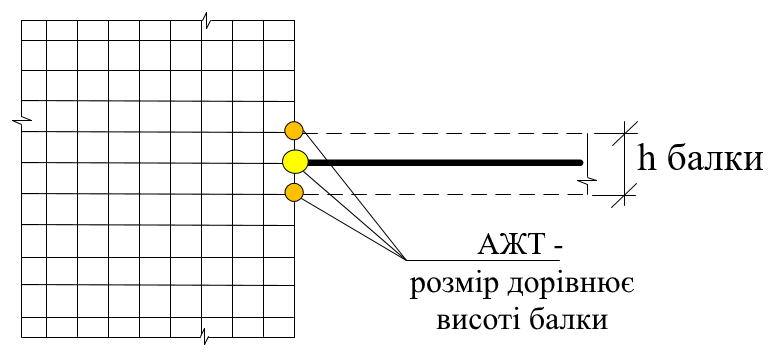
Інший спосіб - ввести абсолютно жорстке тіло (АЖТ) у місці примикання балки до діафрагми (висота АЖТ має бути рівною висоті балки, провідний вузол розташований у центрі ваги перерізу балки) (рис. 11). Це забезпечить кінематичну зв'язок між вузлами діафрагми та балки [11].

Як правило збільшення кількості ступенів свободи збільшує точність розв'язання задачі. З шостим ступенем свободи справа трохи інакша.

Приклад 4 – прямокутна балка-стінка, жорстко підвішена по боках, під дією рівномірно-розподіленого навантаження, розташованого на верхній стороні

Розглянемо задачу (рис. 12), яка має точне розв'язання [3].

Вихідні дані:

Навантаження: рівномірно розподілене навантаження, що діє в площині балки-стінки по осі Y: p = 500 Н/м.

Розміри: h = 0.1 м; b = 1.6 м; а = 1.6 м.

Характеристика матеріалу: Е = 2.65 х 10⁶ Па; ν = 0.15.

Граничні умови: балки-стінка жорстко підвішена по боках.

Розрахункова схема балки-стінки показана на рис. 12.

Завдання:

Визначити переміщення у вузлі А по осі Z для скінченних елементів балка-стінка при різній густоті сітки та порівняти з точним рішенням (табл. 3).

Табл. 3. Порівняння результатів розрахунку балки-стінки, в ПК ЛІРА-САПР та аналітичного розрахунку

У табл. 3 наведено значення переміщення по осі Z у вузлі А для різних КЕ-сіток з різними типами скінченних елементів плоскої задачі:

1. КЕ 21 з двома ступенями свободи у вузлі (X, Z);
2. КЕ 28 – прямокутний КЕ плоскої задачі (балка-стінка) з проміжними вузлами на сторонах, з двома ступенями свободи у вузлі (X, Z);
3. КЕ 21 з трьома ступенями свободи у вузлі (X, Z та наявність шостого ступеня свободи UY).

Аналізуючи результати, наведені в табл.3, можна відмітити, що введення шостого ступеня свободи не покращує точність рішення, хоча кількість ступенів свободи збільшується. Також слід враховувати, що зі збільшенням загальної кількості невідомих L обумовленість матриці К погіршується, а це може призвести до неможливості досягнення заданої точності, хоча порядок апроксимації для типів елементів, що використовуються, може обумовлювати цю точність. Критерієм обумовленості матриці може служити спектральне число обумовленості а(К). Чим гірша обумовленість, тим більше а(К). У роботі [9] дається оцінка а(К), яка при рівномірній сітці має вигляд:

де m – порядок системи рівнянь;

h – максимальний розмір скінченних елементів.

З оцінки (2) видно, що при конкретних розрахунках великих задач краще уникати надмірно густих розрахункових сіток, а задану точність досягати за рахунок більш високого порядку апроксимації.

Висновки:

1. У деяких випадках (рис.3, 7) запровадження шостого ступеня свободи має певний сенс. Хоча і в цьому випадку запровадження певних прийомів адекватного моделювання дозволяє уникнути необхідності використання шостого ступеня свободи.
2. При моделюванні конструктивних рішень защемлення (рис.8) застосування шостого ступеня свободи призводить до неправильних результатів.
3. Використання шостого ступеня свободи для поліпшення точності розв'язання задачі (рис.12) призводить до зворотних результатів: загальна кількість ступенів свободи збільшується, а точність погіршується.

Література

1. Городецкий А.С., Барабаш М.С., Сидоров В.Н. Компьютерное моделирование в задачах строительной механики Учебное пособие. / А. С. Городецкий, М. С. Барабаш, В. Н. Сидоров – М.: Издательство АСВ, 2016. – 338 с.
2. Городецкий А.С. Компьютерные модели конструкций / А. С. Городецкий, И. Д. Евзеров. – [2-е изд., доп.] – Киев: "ФАКТ", 2007. – 394 с.
3. Калманок А.С. Расчет балок-стенок / А.С. Калманок – Москва: Госстройиздат, 1956.
4. Allman, D. J. (1984) A compatible triangular element including vertex rotations for plane elasticity analysis. Computers and Structures, vol. 19, pp. 1–8.
5. Расчет и проектирование конструкций высотных зданий из монолитного железобетона: проблемы, опыт, возможные решения и рекомендации, компьютерные модели, информационные технологии / [А. С. Городецкий, Л. Г. Батрак, Д. А. Городецкий и др.]. – Киев: Факт, 2004. – 106 с.
6. Hughes, T. J. R.; Brezzi, F. (1989): On drilling degrees of freedom. Computer Methods in Applied Mechanics and Engineering, vol. 72, pp. 105–121.
7. Hughes, T. J. R.; Brezzi, F.; Masud, A.; Harari, I. (1989): Finite element with drilling degrees of freedom: Theory and numerical evaluations. In Proceedings of the fifth international symposium on numerical methods in engineering, pp. 3-17. Computational mechanics publications, Ashurst, U.K.
8. Ibrahimbegovic, A.; Taylor, R. L.;Wilson, E. L. (1990): A robust quadrilateral membrane finite element with drilling degrees of freedom. International Journal for Numerical Methods in Engineering, vol. 30, pp. 445–457.
9. Розин Л. A. Основы метода конечных элементов теории упругости / Леонид Александрович Розин. – Л. : Из-во ЛПИ, 1971. – 77 с.
10. Барабаш М.С. Компьютерное моделирование процессов жизненного цикла объектов строительства: Монография/ Мария Сергеевна Барабаш. – К.: Изд-вл «Сталь», 2014. – 301 с
11. Киpьязев П.Н. Компьютерные модели узлов примыкания перекрытия к диафрагме / П. Н. Киpьязев, Ю. В. Гензерский, М. А. Ромашкина // Науково-технічний збірник: Проблеми розвитку міського середовища. – К.: НАУ, 2014. – № 2 (12) – С. 236 – 246.
12. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа / А.В. Перельмутер, В.И. Сливкер. - K .: Сталь, 2002 .-- 600 с