Принцип "Визначальне навантаження"

Сучасні програмні комплекси дозволяють проводити комп'ютерне моделювання процесів життєвого циклу конструкцій - процесів навантаження, процесів зведення, процесів динамічного впливу, різних форс-мажорних ситуацій та ін.

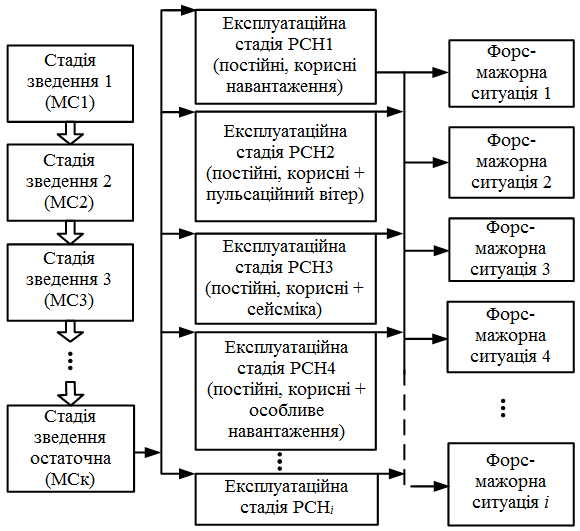
На рис.1 наведено структурну методологічну схему моделювання будівельного об'єкту з урахуванням усіх процесів зміни напружено-деформованого стану конструкцій на кожній стадії.

Стадії монтажу відповідають послідовності зведення конструкції, кожна з яких «зберігає» історію навантаження. Стадії послідовно змінюють одна одну, відповідно зведена конструкція на кожній стадії має змінене НДС. Остання MC_k стадія відповідає зведеній конструкції, та її НДС «зберігає» всю інформацію послідовності зведення, пов'язану із змінами конструктивної схеми, додаванням та зняттям монтажних навантажень і т.п.

Стадія МС_k є стартовою для розрахунку на експлуатаційні навантаження. НДС на експлуатаційних стадіях визначається розрахунком на різні сполучення навантажень (РСН₁ – експлуатаційні статичні навантаження; РСН₂ – корисні навантаження з урахуванням пульсаційної вітрової складової, РСН₂ – корисні навантаження з урахуванням сейсмічного впливу та ін.). Деякі експлуатаційні стадії, у свою чергу, є стартовими для моделювання форс-мажорних ситуацій.

Звичайно, таке моделювання, навіть з урахуванням зростаючих можливостей сучасних комп'ютерів, є громіздким крім великої кількості розрахунків різних конструктивних схем, кожен з них, як правило, треба проводити з урахуванням геометричної, фізичної, конструктивної, генетичної нелінійності. Особливо це стосується форс-мажорних ситуацій, коли необхідно визначати додаткові резерви несучої здатності конструкції з метою не допустити прогресуючого обвалення при мінімальних додаткових витратах матеріалів. Крім того, визначення НДС конструкції на експлуатаційних стадіях повинно враховувати тимчасові зміни реологічних властивостей матеріалу (усадка, повзучість та ін.), що також обумовлює необхідність проведення розрахунку в нелінійній постановці [4].

Проведення такого розрахунку все-таки є досить громіздким і в даний час застосовується лише при проектуванні унікальних об'єктів, що не мають аналогів. Як правило, переважну більшість розрахунків проводять за традиційною схемою (рис.2).

Розрахунок у лінійній постановці не враховує ряд важливих факторів, наприклад, фізичну нелінійність залізобетону. Цей фактор зумовлює не тільки значне збільшення переміщень (у 2-3 рази порівняно з розрахунком у нелінійній постановці), а й перерозподіл зусиль, що адекватно відображає дійсну роботу конструкцій.

Принцип «визначальне навантаження» з одного боку реалізує врахування різних факторів, недоступних при розрахунку в лінійній постановці, з іншого боку зберігає традиційну технологію розрахунку (рис.2).

Приклад принципу «Визначальне навантаження» у методиці «Інженерна нелінійність»

Приклад застосування принципу «Визначальне навантаження» при призначенні коефіцієнтів пружної основи

Величини коефіцієнтів пружної основи залежать від глибини стискуваної товщі, яка в свою чергу залежить від навантаження. Таким чином, це обумовлює нелінійну постановку задачі.

Приклад принципу «Визначальне навантаження» дозволяє здійснити розрахунок за наступною схемою:

1. Попередньо призначаємо рівномірне напруження під підошвою фундаменту шляхом розподілу маси будівлі на площу фундаменту (крок 1, рис.3). Отримуємо змінні коефіцієнти пружної основи по площі фундаменту від рівномірного напруження під підошвою. Прикладаємо відсіч ґрунту від обраного визначального навантаження (крок 2-4, рис.3).
2. Визначаємо коефіцієнти пружної основи для кожного скінченного елементу фундаментної конструкції від нерівномірного напруження під підошвою фундаменту (крок 5, рис.3).
3. Розрахунок за традиційною схемою на всі навантаження з урахуванням знайдених у п. 2 коефіцієнтів пружної основи.

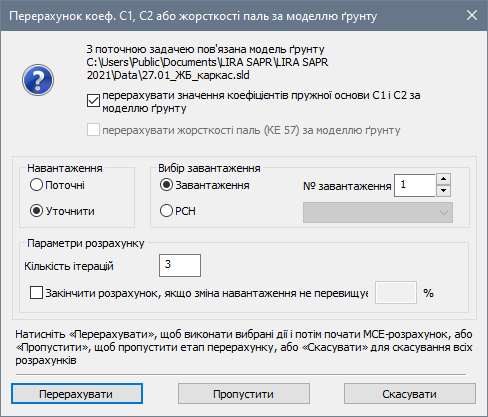
При моделюванні пальових фундаментів у ПК ЛІРА-САПР є можливість уточнювати навантаження на оголовки паль для перерахунку жорсткостей (жорсткості змінюються з урахуванням взаємовпливу осадки в групі паль, оскільки змінилися навантаження на оголовки сусідніх паль). Починаючи з версії ЛІРА-САПР 2019 реалізований інструмент для автоматизації виконання ітераційних розрахунків (без участі користувача) (рис.4).

Застосування принципу «Визначальне навантаження» при призначенні розмірів полиць для балкового ростверку

Посилення плит балками досить часто зустрічається у сучасному житловому будівництві. Розташування балок, як правило, нерегулярне, немає чітко вираженої системи головних та другорядних балок, балки можуть мати невелику висоту, і тут часто навантаження передаються на опори за рахунок роботи як плити, так і за рахунок балок.

У цьому випадку досвід розрахунку та проектування ребристих перекриттів (ці приклади є в кожному підручнику з залізобетонних конструкцій, де рекомендується збирати навантаження з плити на другорядні балки, вважаючи спирання плити на них жорстким, потім розрахувати другорядні балки, вважаючи їх спирання на головні балки жорстким і т. д.) малопридатний і може мати хіба що антикварну цінність.

З іншого боку, з точки зору методу скінченних елементів начебто не повинно бути жодних проблем: вводиться скінченно-елементна сітка плити з базовими точками на лініях балок, навантаження прикладається по верху плити і т.д. Але тут виникає багато проблем, пов'язаних зі стиковкою в скінченно-елементної моделі елементів різної мірності. Головна проблема тут – як призначити жорсткість балки.

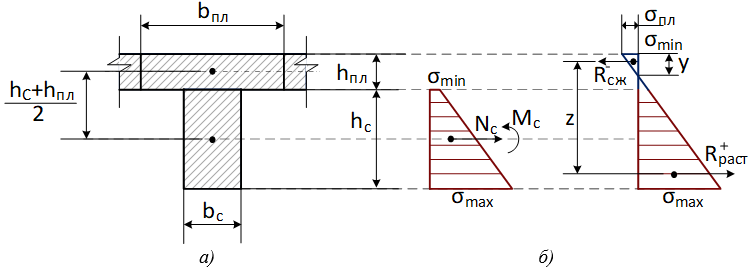
Якщо в скінченно-елементну модель плити, вузли сітки якої лежать на серединній поверхні, ввести стержні перерізом h_сxb_с, то буде розрахована система із взаємним розташуванням плити та балки, представленим на рис.5б. Звичайно, така модель не витримує жодної критики. Можна ввести тавровий переріз балки. Взаємне розташування плити та балки в цьому випадку представлене на рис.5в. Але тут виникає питання про те, як призначити ширину полиці. Різні методичні матеріали дають різні рекомендації – від 6 до 15 товщин плити. Крім того, по цій схемі робота плити враховується двічі. Щоправда, це цілком припустимо, оскільки скінченні елементи плити моделюють згинальну групу зусиль, а частина плити у складі полиці балки моделює мембранну групу зусиль, яка викликає в плиті невеликі напруження у порівнянні з напруженнями від згинальної групи. Досить адекватною є модель, запропонована в [10], де взаємодія плити та балки представлена на рис.5г.

У цьому випадку стержні перерізом h_сxb_с, підвішуються за допомогою абсолютно жорстких вставок до вузлів скінченно-елементної моделі плити, що лежать у її серединній поверхні. Тут (на відміну від моделей рис. 5б і рис. 5в, де в скінченних елементах плити та стержнів виникає лише згинальна група зусиль, а кожен вузол скінченно-елементної схеми має три вузлові невідомі – вертикальне переміщення і два кути повороту) кожен вузол скінченно-елементної схеми має п'ять вузлових невідомих – три лінійних переміщення і два кути повороту, а скінченні елементи плити випробовують крім згинальної також мембранну групу зусиль, а в стержневому елементі, крім згинального моменту (М_с) та поперечної сили, виникає ще й нормальна сила (N_с).

Хоча остання модель найбільш повно відображає дійсну роботу конструкції, і знімає питання про призначення ширини полиці у тавровій балці, разом з тим на останніх етапах проектування балки виникають труднощі. Звичайно, можна просто розрахувати переріз стержня h_сxb_с, на отримані у ньому зусилля М_c, і N_c. Однак, як правило, значення N_c велике, і переріз буде законструйований як позацентрово розтягнутий елемент, а підібрана арматура в ньому буде розподілена по всьому периметру, у той час як за правилами конструювання балкових ростверків арматура має бути розташована біля нижньої та верхньої грані. Таким чином, для конструювання бажано розглядати тавровий переріз балки, підданий згину, проте неясно, який згинальний момент діє на балку і який переріз балки треба розраховувати. В даному випадку можна розглядати наступний інженерний підхід, заснований на гіпотезі про те, що рівнодіюча мембранна сила плити, яка врівноважує нормальну силу у підвішеному стержні (N_с), прикладена в центрі плити (точка А рис.6а). Тоді можна вважати, що згинальний момент, який діє на балку таврового перерізу, дорівнює М_б=М_с+N_сх0,5(h_с+h_n). Залишається тільки визначити ширину полиці таврової балки. Тут можна з деякою натяжкою використати вище прийняту гіпотезу: якщо центр тяжіння мембранних сил прикладений у центрі плитної частини (точка А), то полиця має бути рівномірно стиснута. Так як арматура розраховуватиметься в рамках припущень про граничний стан перерізу, то напруження в полиці буде R_б. Тому ширина полиці b<_n = N_c/(h_nR_б).

Поперечна сила в балці визначається як перша похідна (при чисельних розрахунках використовується скінченнорізницевий підхід) від моментів М_б(х). Так як епюри М_с и N_с у стержні мають ступінчастий вид, тобто в кожному перерізі є два значення моменту та нормальної сили, то їх слід або усереднити, або брати їх значення у серединах відрізків. Звичайно, припущення про те, що напруження в полиці для визначення М_б, прийняті постійними, а при визначенні b_n, рівні R_б, у ряді випадків можуть виявитися недостатньо вдалими, тому нижче наводиться дещо інший підхід, що ґрунтується на гіпотезі плоских перерізів (рис.6б). Деформація перерізу визначається на основі епюри напружень у перерізі стержня:

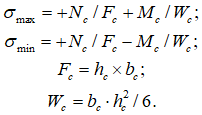
Далі нахил перерізу продовжується в область плити та з геометричних співвідношень визначається .

Після цього визначення М_б і b_n представляється справою техніки:

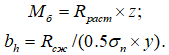
В даному випадку принцип «визначальне навантаження» дозволяє провести розрахунок за наступною схемою.

1. Призначення визначального навантаження.
2. Визначення ширини полиці за вищезгаданою методикою для кожної ділянки балкового ростверку.
3. Розрахунок балочного ростверку на всі навантаження з призначеними по п. 2. розмірами полиць.

Висновок: Розглянуті приклади застосування принципу «визначальне навантаження», мабуть, не вичерпують усі області його застосування. Інженерна практика підказуватиме ці області, які й реалізовуватимуться в ПК ЛІРА-САПР.

Література

1. Барабаш М. С. Влияние процесса возведения на пространственную работу несущих систем зданий / М. С. Барабаш // Строительство, материаловедение, машиностроение // Сб. научн. Трудов. – Дн-вск: ПГАСА, 2012. – № 65. – С. 29 - 34.
2. Барабаш М. С. Компьютерное моделирование процессов жизненного цикла объектов строительства: Монография / Мария Сергеевна Барабаш. – К.: «Сталь», 2014. – 301 с
3. Бондаренко В. М. Инженерные методы нелинейной теории железобетона / В.М. Бондаренко – М.: Стройиздат, 1982. – 287 с.
4. Городецкий А. С. Компьютерные модели конструкций / А. С. Городецкий, И. Д. Евзеров. – [2-е изд., доп.] – Киев: "ФАКТ", 2007. – 394 с.
5. Городецкий А. С., Барабаш М. С. Компьютерное моделирование процесса возведения строительных конструкций / А. С. Городецкий, М. С. Барабаш // Строительная механика и расчет сооружений: Научно-технический журнал. – Москва: ЦНИИСК им. В. А. Кучеренко, 2014. – Вып. 5 (256). – С. 28–33.
6. Городецкий А.С., Барабаш М.С., Сидоров В.Н. Компьютерное моделирование в задачах строительной механики Учебное пособие. / А. С. Городецкий, М. С. Барабаш, В. Н. Сидоров – М.: Издательство АСВ, 2016. – 338 с.
7. Городецкий А. С. К расчету физически нелинейных плоских рамных систем /А. С. Городецкий, В. С. Здоренко // Строительная механика и расчет сооружений. – 1969. – № 4. – С. 61-68.
8. Городецкий А. С. Компьютерное моделирование процесса нагружения железобетонных конструкций. Сборник научных трудов Луганского национального университета, серия «Технические науки» N49/52, - Л.: Из-во «ЛНАУ», 2004, с.3-10.
9. Городецкий А. С. Учет нелинейной работы железобетонных конструкций в практических расчетах / А. С. Городецкий, М. С. Барабаш // Строительство, материаловедение, машиностроение // Сб. научн. Трудов. – Дн-вск: ПГАСА, 2014. – Вып. 77. – С. 54–59.
10. Метод конечных элементов: теория и численная реализация / [Городецкий А. С., Евзеров И. Д., Стрелец-Стрелецкий Е. Б. и др.]. – К. : Факт, 1997. – 138 с. – (Программный комплекс ЛИРА-Windows).
11. Пикуль А. В. Определение жесткостных характеристик сечения железобетонного стержня с учетом нелинейных свойств материала / А.В. Пикуль, Д.А. Городецкий // Актуальные проблемы компьютерного моделирования конструкций и сооружений: тезисы докладов IV Международного симпозиума. – Челябинск.: Издательский центр ЮУрГУ, 2012. – С. 228.