Heat Transfer Analysis

General principles

In heat transfer analysis, temperature in analytical model nodes is unknown (similar to displacement in structural analysis). Consequently, the equilibrium equation may be written as:

Thermal analysis	Structural analysis

Thermal conductivity matrix is formed from the thermal conductivity coefficients K, which are specified in the stiffness of the finite element. In the case of plates, the thermal conductivity matrix is multiplied by the thickness of the element H.

Picture 1. Material properties of a plate finite element

To investigate the transient heat transfer process, the specific heat matrix (equivalent to the damping matrix in structural analysis) must be included into the equilibrium equation:

The specific heat matrix depends on the product of the specific heat coefficient C and density of the material R_O. In case of plates, the specific heat matrix is multiplied by the thickness of the element H.

Picture 2. Material properties of a plate finite element

Thermal finite element types

Thermal conduction finite elements
No. 1505
	Two-node thermal conduction finite element
No.1508
	Three-node thermal conduction finite element
No.1509
	Four-node thermal conduction finite element
No.1512
	Tetrahedral thermal conduction finite element
No.1514
	Six-node thermal conduction finite element
No.1516
	Eight-node thermal conduction finite element
Thermal convection finite elements
No.1551
	One-node thermal convection finite element
No.1555
	Two-node thermal convection finite element
No.1558
	Three-node thermal convection finite element
No.1559
	Four-node thermal convection finite element

Load types

Steady-state load types

1. Temperature on node (Derichlet's boundary condition) When the value of temperature in some node is determined: , '' It is similar to initial displacements in structural analysis.

Picture 3. Loads on nodes

 

2. Heat flux (Newmann's boundary condition)

When external load is determined:

By definition, heat flux is the amount of heat that is transferred per unit of area and per unit of time in some material.

It is measured in (or , because 1 W = 1 ).

In 'LIRA-SAPR' there is an opportunity to apply the heat flux on nodes, plates or tridimensional bodies. The heat flux applied on nodes called the heat flow and measured in .

2.1. Heat flow (heat flux applied on a node)

To apply the heat flux on a node, one has to evaluate the surface area, through which the heat transfers (for a beam it would be the cross-section area). For example, if the value of the heat flux      q = 100 , and the area through which the heat transfers is 0.1 m², then the value of the defined load on the node P is 100*0,1 = 10 .

Heat flow

 

 

2.2. Heat flux applied on edge

To apply the heat flux on edge, one has to multiply the value of the heat flux by the plate thickness. For example, if the value of the heat flux q = 100 , and the thickness of the plate is 0,1 m, then the value of the applied load P is equal to 100*0,1 = 10 .

  

Heat flux applied on edge

 

 

 

 

2.2. Heat flux applied on a solid body

To apply the heat flux on a side plane, one doesn't have to multiply the value of the heat flux neither by area nor by length 🙂. One just has to define the value of the applied heat flux (for example q = 100 ), and the number of the side plane on which the flow is applied.

Heat flux applied on a side plane

 

3. Convection (or Newton's boundary condition)

External load is determined:

Convection heat transfer is the process of heat loss by a solid body caused by moving of fluids (gases and liquids). It happens when individual particles with different temperatures come into contact to each other. During convection, heat passes from the surface of the body to the moving environment (for example air).

One applies the convective load on the analytical model in two steps:

At the first step, it is necessary to create a convective finite element at a place of contact between analytical model and air.

For a bar ' contact is modeled by one-node convective FE (FE No. 1551).

For a plate ' contact is modeled by two-node convective FE (FE No. 1555).

For a volume body ' by plate convective FE (FE No. 1558 and No. 1559).

Within stiffness of convective finite element, it is necessary to define the heat transfer coefficient (film coefficient) and the area of the contact surface (for one-node FE) or the height of the contact surface (for two-node FE). The heat transfer coefficient h is measured in .

Contact surface

Picture 4. Convection heat transfer

At the second step, it is necessary to apply a load on the convective contact element. The external air temperature is modeled through the applied load.

Picture 5. External temperature

The examples of applying of convective load you may find further in the text in sections "Example 1. Steady-state heat transfer analysis" and "Example 2. Transient heat transfer in fire resistance analysis".

Transient load types

From all types of transient loads, only the time-dependant heat flow can be applied directly on a node (or an element). All other types of unsteady loads can be specified only by using the dialog box called 'Time history analysis from static load cases'.

1. Time dependant Heat flux.

1.1. On node

There are three types of time-dependant loads on node (similar to the structural analysis): polyline with arbitrary step; sinusoidal; polyline with equal step.            The value of the applied load is determined similarly to the steady-state heat flux, in other words, the value of the heat flux is multiplied by the surface area, through which the heat transfers. Transient heat flow (transient heat flux on node)

Picture 6. Unsteady load types

1.2. On a plate edge or on a volume body side plane

The load, which is specified in the stationary load, is multiplied by this coefficient z(i)

To apply transient heat flux on a plate edge or on a face of a solid finite element, one has to apply steady-state heat flux in any 'Load case', except 'Load case No. 4'. Since the 'Load case No. 4' is intended to specify only the damping loads. After that, in the window called 'Time history analysis from static load cases' (see Pic. 7), one has to modify a transient load type from the corresponding steady-state one, by specifying the law of time-dependant load variation. The following transformation laws can be used to modify heat flux: polyline with arbitrary step (1); sinusoidal (2); polyline with equal step (4).

Picture 7. Generation of the transient heat flux

2. Time dependant Convection.

(convective heat flux)

This type of load can be used if the temperature of the moving fluid (for example, air) is much variable in time.

One can define the transient convection in the same way as the transient heat flux on a plate edge or on a face of a solid finite element (that is, to modify a steady-state convection into the transient one).

3. Time dependant Radiation.

(radiative heat flux)

When external load is determined:

is the configuration factor;

is the surface emissivity of the member;

is the emissivity of the fire;

is the Stephan Boltzmann constant (= );

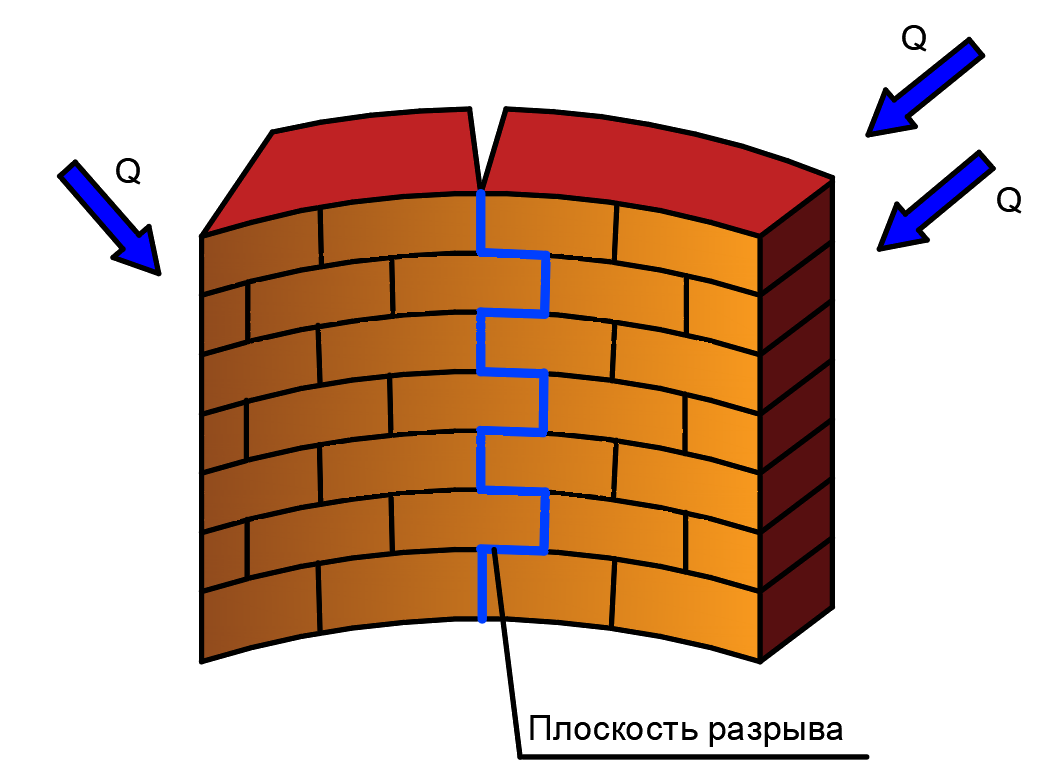is the temperature of the environment [ ];

is the surface temperature of the solid body [ ].

Radiative heat flux occurs due to the fact that the part of the thermal (internal) energy of the body (which exists due to the mechanical motin of elementary particles of the body) is transformed into radiation energy. Radiation energy is the energy of electromagnetic oscillations with waves of different lengths. Electromagnetic waves arise due to the oscillation of charged particles (electrons or ions) which are part of the body. When radiation energy arrives at a body, one part of this energy is absorbed by the body, another part passes through the body, and some part is reverberated. The degree of absorption of the radiation energy could be taken into account through the coefficient . For example, for concrete, this coefficient is equal to 0.75, and for blackbody it is equal to 1.

The configuration factor ' is usually equal to 1, it introduces the location of the radiation source in relation to the absorber material.

The example of applying the radiation load you may see in the section "Example 2. Transient heat transfer in fire resistance analysis".

In summary, heat is the energy that arises due to the movement of tiny particles of the body (atoms, molecules or ions). Basically, there are three main types of heat transfer: heat conduction, convection and radiation.

1. Thermal conduction. In this case, a body transfers heat by chaotic motion of particles, from a more heated part of the body to a less heated one.	Thermal conduction
2. Convection. It is a kind of heat transfer, that occurs due to the moving of fluids (gases and liquids) adjacent to the body.	Convection
3. Radiation. In this case, heat is transferred by the electromagnetic waves.	Radiation

---