Objective
To determine the stress–strain state of a narrow cantilever plate subjected to a couple of forces that cause torsion.
Reference
J. Robinson, Element evaluation. A set of assessment parts and tests, Proceeding of Finite Element Methods in the commercial environment, vol. 1, October 1978.
J.L. Batoz et M.B. Tahar, Evaluation of new quadrilateral thin plate boundary element, International Journal for numerical methods in engineering, vol. 18, Jon Wiley & Sons, 1982.
Problem statement
To determine the vertical displacement Z at the corner of the free edge of the plate (point C).
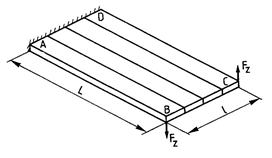
Design model
A narrow cantilever plate subjected to vertically applied, balanced concentrated loads acting at the corners of the free edge.
|
a |
b |
Geometry
Plate thickness h = 0.05 m;
Cantilever projection L = 12 m;
Relative thickness h/L = 0.0042;
Plate width l = 1 m.
Material properties
Modulus of elasticity Å = 1.0 * 107 Pa;
Poisson's ratio ν = 0.25.
Boundary conditions
Along segment AD, the plate finite elements are fully fixed in all degrees of freedom (X, Y, Z, uX, uY, uZ).
Loads
Vertical concentrated load Fz = 1 N.
Note
The problem is solved in a 3D formulation (model type 5).
The model is generated with FE type 41 – arbitrary rectangular FE of shell.
The FE mesh consists of:
– 50 elements along the cantilever length;
– 16 elements across the width.
Size of finite elements 0.24 × 0.0625 m.
Nodes: 867. Elements: 800.
Output data
Comparison of calculation results
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % |
| Ñ | w, m | 0,03537 | 0,03533 | 0,1131 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.



Comments