Objective
To determine the stress–strain state of a torus subjected to internal pressure.
Reference
R.J. Roark et W.C. Young, Formulas for stress and strain, 5e edition, New York, McGraw-Hill, 1975.
Problem statement
To determine the radial displacements ΔR at the inner and outer guides of the torus, as well as the stresses σ11 and σ22 in the torus wall.
Design model
The torus is free of restraints and is subjected to a uniform internal pressure q.
|
a |
b |
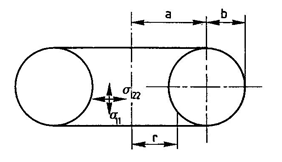
Geometry
Radius of generatrix b = 1 m;
Distance from the axis of revolution to the centre of the generatrix a = 2 m;
Wall thickness h = 0,02 m.
Material properties
Modulus of elasticity Å = 2,1 * 1011 Pa.
Poisson's ratio ν = 0,3.
Boundary conditions
Symmetry restraints.
Loads
Uniformly distributed across the area P = 10000 Pa.
Note
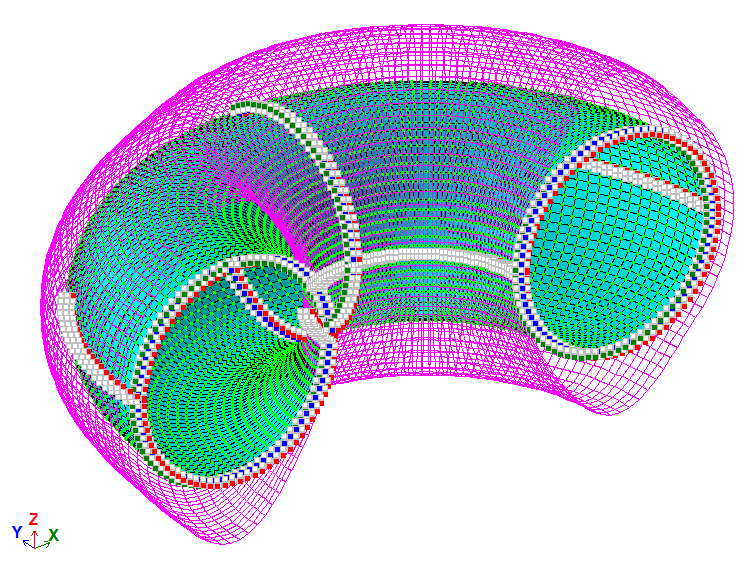
The problem is solved in a 3D formulation (model type 5).
The model is generated with FE type 44 – arbitrary quadrilateral FE of shell.
A fragment of the torus (180°) is considered in the design model. Symmetry restraints are applied to account for the truncated part of the torus.
The finite element mesh consists of:
– 80 elements along the circumference of the cross-sectional circle;
– 90 elements along the circumference of the torus wall.
Nodes: 7280. Elements: 7200.
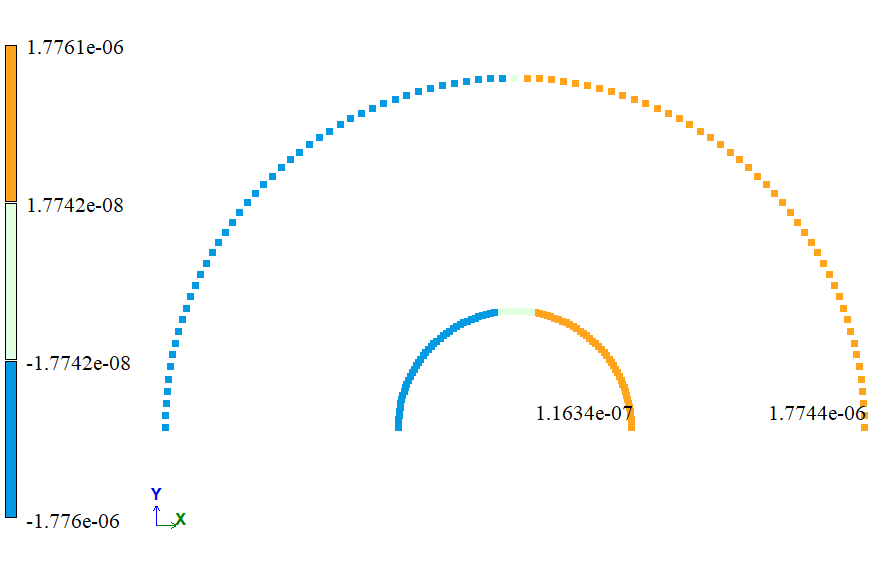
Output data
|
a |
b |
Analytical solution
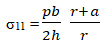

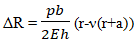
Comparison of calculation results
Without additional side nodes:
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % |
| ∀r | σ22, Pa | 2,5 * 105 | 2,4915 * 105 | 0,34 |
| r = a - b | σ11, Pa | 7,5 * 105 | 7,4917 * 105 | 0,1107 |
| ΔR, m | 1,19 * 10-7 | 1,1634 * 10-7 | 2,2353 | |
| r = a + b | σ11, Pa | 4,17 * 105 | 4,1663 * 105 | 0,0887 |
| ΔR, m | 1,79 * 10-6 | 1,7744 * 10-6 | 0,8715 |
With additional side nodes:
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % |
| ∀r | σ22, Pa | 2,5 * 105 | 2,4941 * 105 | 0,236 |
| r = a - b | σ11, Pa | 7,5 * 105 | 7,4739 * 105 | 0,348 |
| ΔR, m | 1,19 * 10-7 | 1,2349 * 10-7 | 3,6359 | |
| r = a + b | σ11, Pa | 4,17 * 105 | 4,1668 * 105 | 0,0676 |
| ΔR, m | 1,79 * 10-6 | 1,7732 * 10-6 | 0,9385 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.



Comments