Objective
To determine the stress–strain state of a cylinder with free ends subjected to internal pressure.
Reference
Warren C. Young, Richard G. Budynas. Roark’s Formulas for Stress and Strain. Seventh Edition. New York, McGraw-Hill, 2002.
Problem statement
To determine the stresses in the cylinder wall in the meridional direction (σ₁) and the circumferential direction (σ₂), as well as the meridional displacements Δy and radial displacements ΔR.
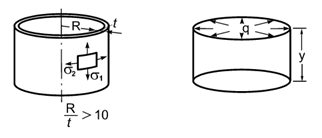
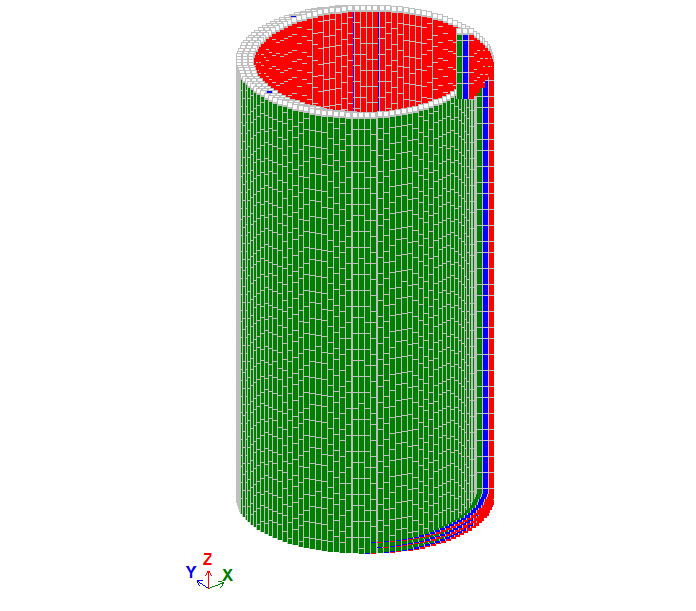
Design model
The cylinder is free of restraints and is subjected to a uniform internal pressure q.
|
Variant 1 |
Variant 2 |
Geometry
Cylinder radius R = 1 m;
Cylinder wall thickness t = 0,02 m;
Cylinder height L = 4 m.
Material properties
Modulus of elasticity Å = 2,1 * 1011 Pa.
Poisson's ratio ν = 0,3.
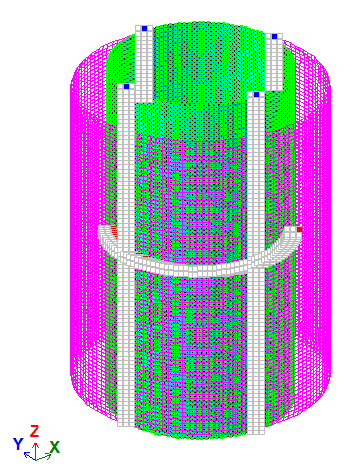
Boundary conditions
Symmetry restraints.
Loads
Internal pressure p = 10000 Pa.
Note
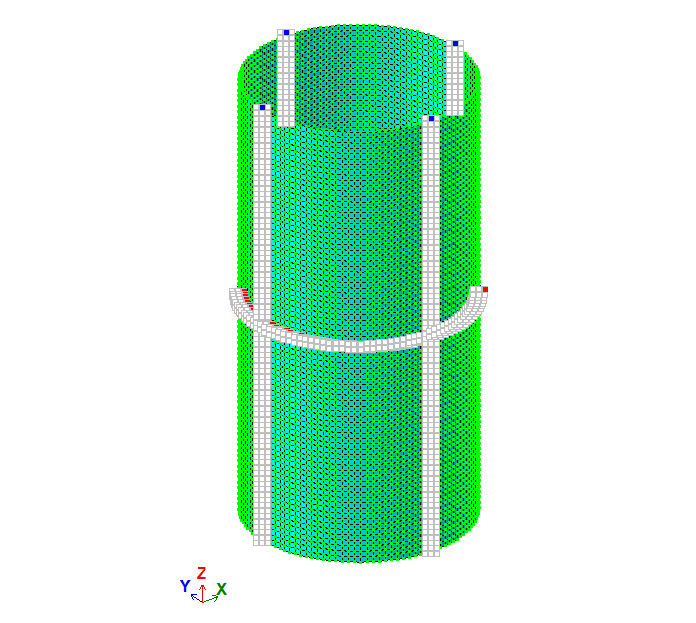
The problem is solved in a 3D formulation (model type 5).
The model is generated with FE type 44 – arbitrary quadrilateral FE of shell.
Two solution variants were considered:
-
Shell membrane theory (Variant 1);
-
General shell theory (Variant 2).
The behaviour of the cylindrical shell according to the membrane theory is achieved by imposing restraints on all rotational degrees of freedom (DOF) at all nodes of the design model.
A local coordinate system is assigned to the nodes of the model (the local X1-axes are directed outward from the cylinder centre).
The finite element mesh consists of:
– 80 elements along the cylinder height;
– 120 elements along the circumference.
Size of finite elements: 0.05 õ 0.0525 m.
Nodes: 9720. Elements: 9600.
Output data
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
Analytical solution
σ1 = p/t
σ2 = 0
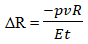
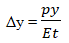
Comparison of calculation results
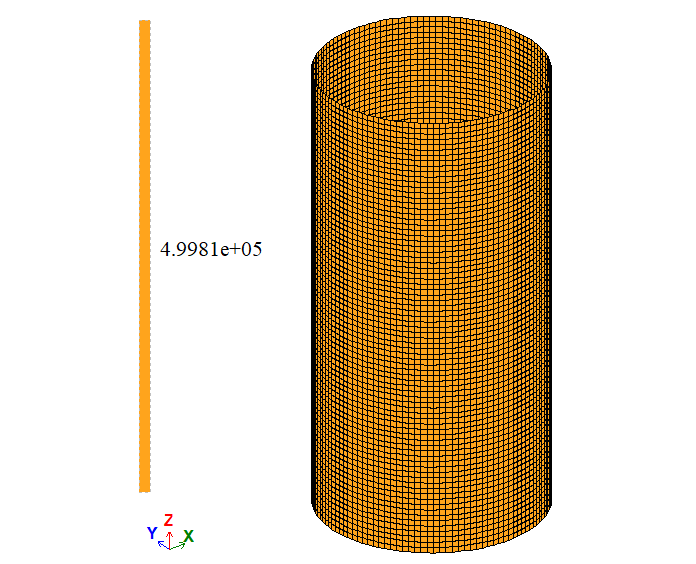
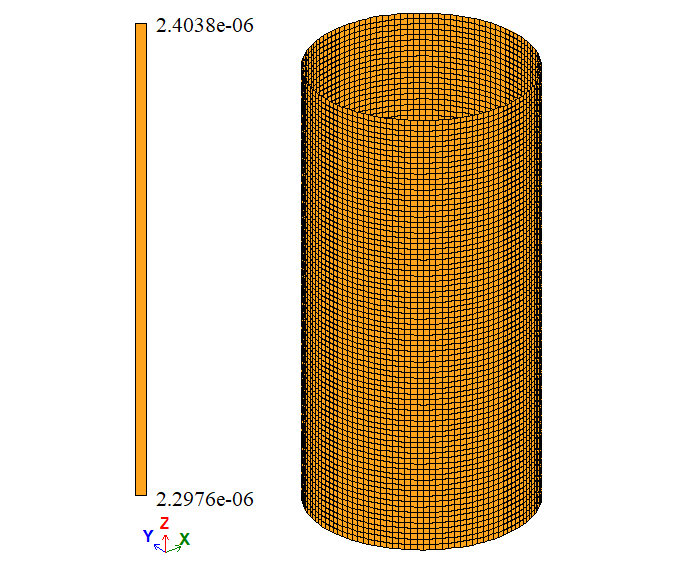
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % | ||
| Variant 1 | Variant 2 | Variant 1 | Variant 2 | |||
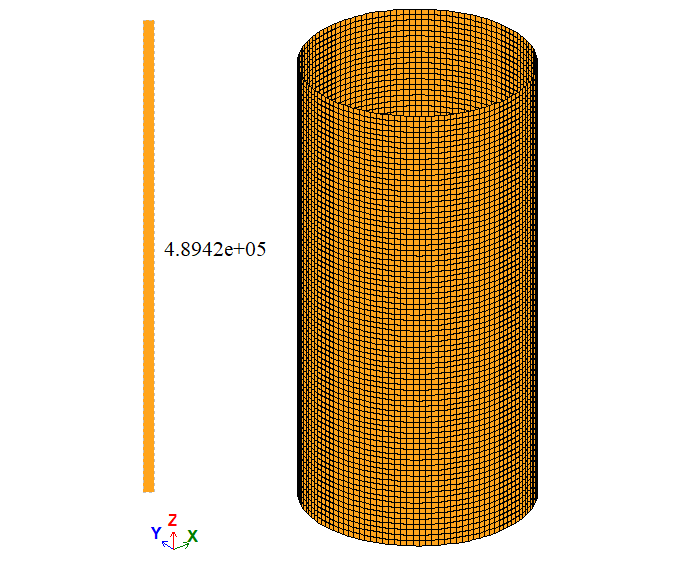
| Point on the surface | σ1, Pa | 5 * 105 | 4,8942*105 | 4,9981*105 | 2,116 | 0,038 |
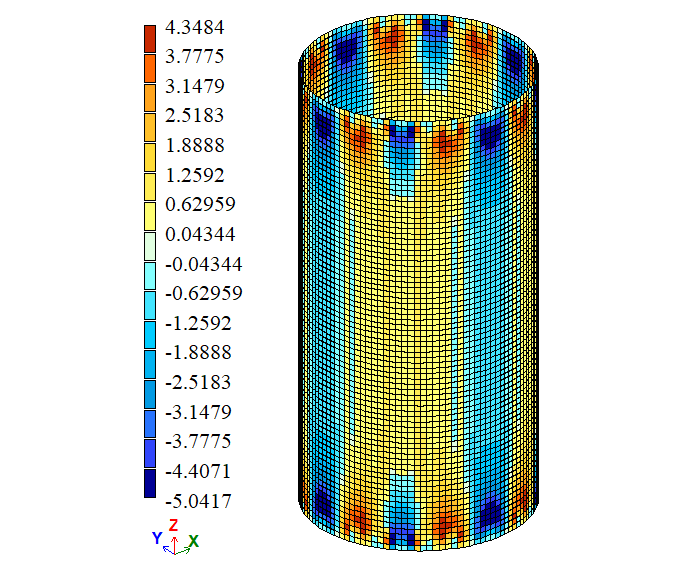
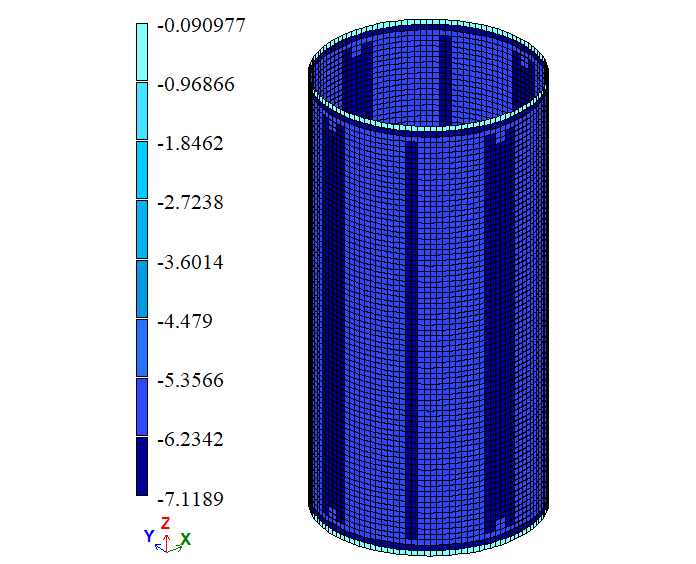
| σ2, Pa | 0 |
-5,0417 4,3484 |
-7,1189 -0,09097 |
- | - | |
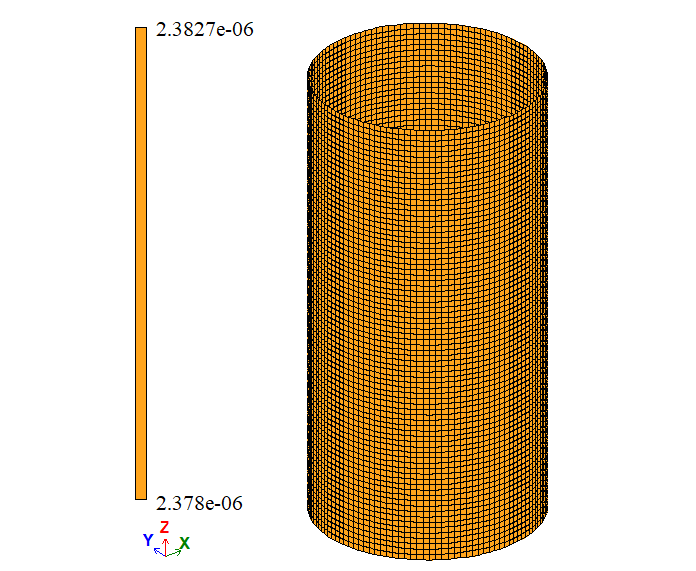
| ΔR, m | 2,38 * 10-6 | 2,3798*10-6 | 2,3803*10-6 | 0,0084 | 0,0126 | |
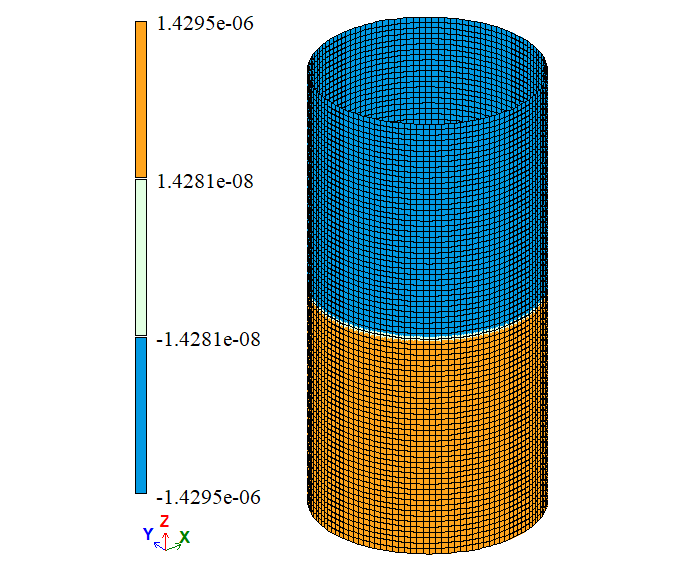
| Δy, m | -2,86 * 10-6 | -2,859 * 10-6 | -2,859 * 10-6 | 0,038 | 0,035 | |
|
Note: As symmetry restraints were used in the boundary conditions (restraint in the Z direction at the cylinder mid-height), the vertical displacement Δy reported in the table has been doubled. |
||||||
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.

Comments