Objective
Combined longitudinal and transverse bending in one plane.
Reference
Strength Calculations in Mechanical Engineering / S. D. Ponomaryov, V. L. Biderman, K. K. Likharyov et al., 1956.
Problem statement
To determine the vertical displacements w(x) and the bending moments M(x) under compressive and tensile axial load.
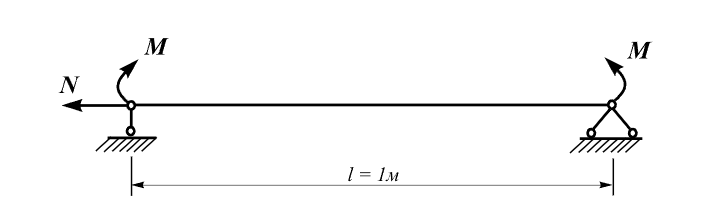
Design model
A beam on two supports subjected to pure bending with an additional axial load.
Geometry
Beam length l = 1,0 m
Cross-sectional area F1 = 1,0 * 10-2 m2
Material properties
Modulus of elasticity E = 2,0 * 1010 Pa
Poisson's ratio μ = 0,3
Moment of inertia of the cross-section I = 8,333 * 10-6 m4
Loads
Concentrated load N = 200 kN
Bending moment M = 10 kN * m
Note
The linear analysis is carried out for an energetically equivalent model in the form of a bar FE on an elastic foundation that resists rotation of its sections with a stiffness coefficient per unit length kφ = N.
The design model is a plane frame; 16 bar elements, type 2; 17 elements type 51, concentrated rotational springs with stiffness CUY = -12,5 kN*m/rad (-6,25 kN*m/rad) for the bar under compression and CUY = 12,5 kN*m/rad (6,25 kN*m/rad) for the bar under tension; 17 nodes.
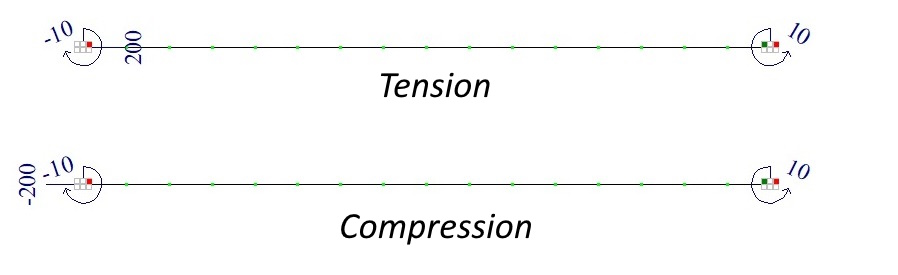
Output data
|
Deflection w under compressive axial load (mm)
|
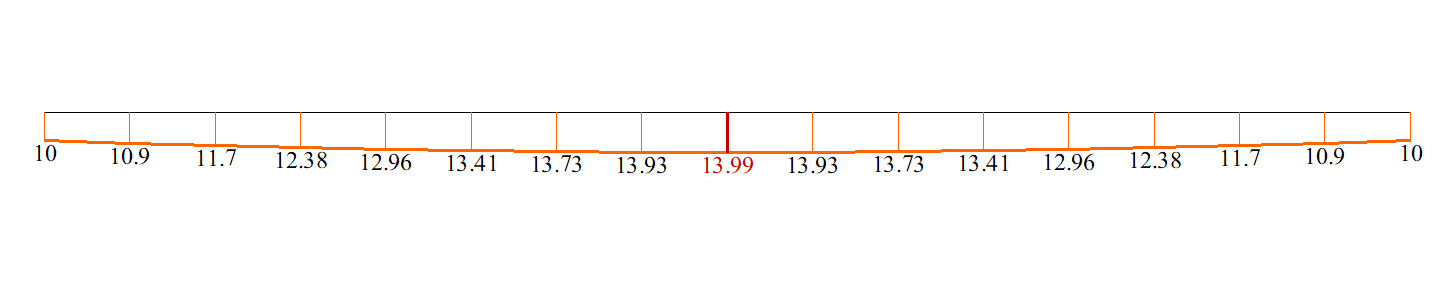
Bending moment M under compressive axial load (kN*m)
|
|
Deflection w under tensile axial load (mm)
|
Bending moment M under tensile axial load (kN*m)
|
Analytical solution
In the analytical solution, the equations of the elastic curve w(x) and the bending moment M(x) under compressive axial load are determined by the following formulas:
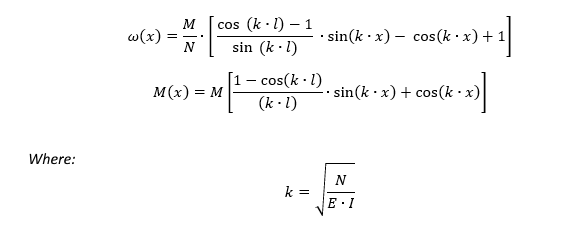
In the analytical solution, the equations of the elastic curve w(x) and the bending moment M(x) under tensile axial load are determined by the following formulas:
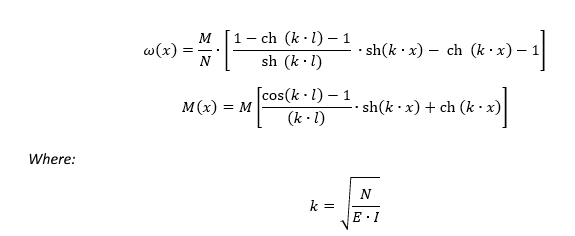
Comparison of calculation results
| Parameter | Compressive axial load | Tensile axial load | ||||
| Analytical solution | SCAD | Error, % | Theory | LIRA-FEM | Error, % | |
| Transverse deflections w(0,5*l), mm | -19,959 | -19,96 | 0 | -11,986 | -11,99 | 0 |
| Bending moment M(0,5*l), kN*m | 13,992 | 13,992 | 0 | 7,603 | 7,603 | 0 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.
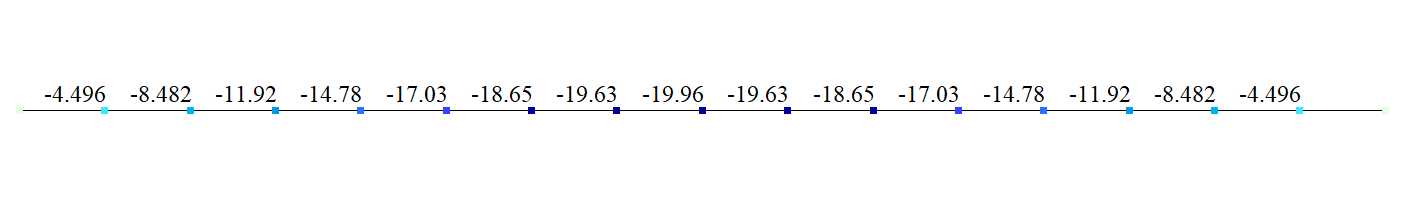
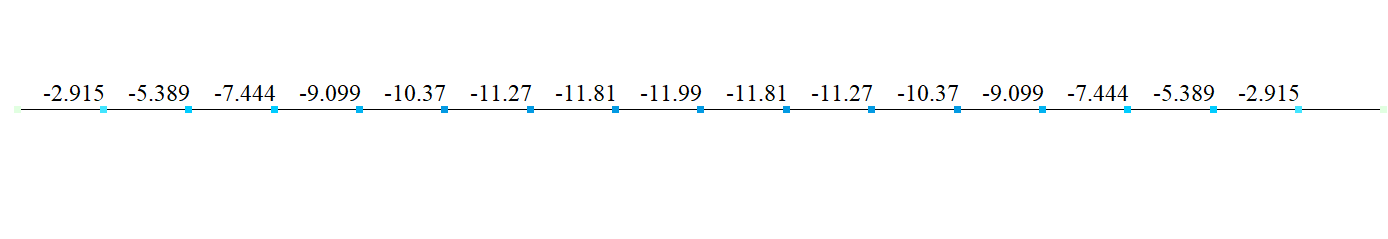

Comments