Objective
To determine the stress state of a beam fixed at both ends under the transverse displacement of one end.
Reference
JM Gere and W. Weaver, Jr., Analysis of Framed Structures, New York, D. Van Nostrand Co., 1965.
Problem statement
To determine the shear force Q and the bending moment M at the displaced end.
Design model
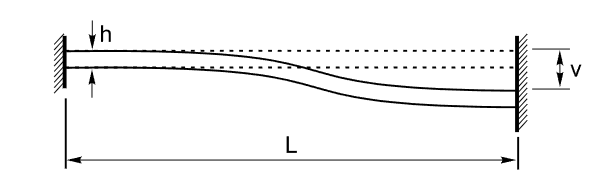
A beam with a rectangular cross-section, fixed at both ends, is subjected to transverse displacement of one end.
Geometry
Beam length L = 80,0 m
Beam cross-section width b = 2,0 m
Beam cross-section depth h = 2,0 m
Value of transverse displacement v = 1,0 m
Material properties
Modulus of elasticity Е = 3 * 107 Pa
Note
The design model is a plane frame consisting of four elements of type 2.
The FE mesh is generated along the longitudinal axis (along the X axis of the global coordinate system) with a step of 20 m.
The boundary conditions at the fixed ends are defined by applying restraints for the U degrees of freedom.
The effect of the specified transverse displacement is modelled by imposing a displacement along the Z axis of the global coordinate system on the corresponding restraint.
Number of nodes in design model: 5.
Output data
Comparison of calculation results
| Parameter | Analytical solution | LIRA-FEM | Error, % |
| Shear force Q at the displaced end, N | 937,5 | 937,5 | 0 |
| Bending moment M at the displaced end, N*m | 37500 | 37500 | 0 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.



Comments