Objective
To determine the stress–strain state of a two-span simply supported beam with an intermediate elastic support subjected to concentrated transverse forces applied at the mid-spans.
Reference
C. Massonnet, Application des ordinateurs au calcul des structures, Paris, Eyrolles, 1968, p. 233.
Problem statement
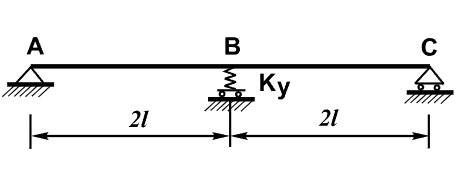
To determine the vertical displacement Z and the vertical reaction N of the intermediate elastic support, as well as the bending moment M in the beam above the intermediate elastic support (point B).
Design model
A two-span simply supported beam with an intermediate elastic support is subjected to concentrated transverse forces F applied at the mid-spans (at a distance l from the end supports).
Geometry
Length of beam span 2l = 6 m
Cross-sectional area A = 0,4762 * 10-2 m2
Moment of inertia for the cross-section I = 6,3 * 10-4 m4
Material properties
Modulus of elasticity Å = 2,1 * 1011 Pa
Stiffness of the intermediate elastic support k = 2,1 * 1011 N/m
Loads
Concentrated transverse forces F = 42 kN
Note
A simple frame consisting of four bar elements of type 2.
The boundary conditions are specified by applying restraints in the X and Z degrees of freedom at the left support A and the right support C, and by imposing a restraint with finite stiffness in the Z degree of freedom at the intermediate support.
Number of nodes in the design model: 5.
Output data
Comparison of calculation results
| Parameter | Analytical solution | LIRA-FEM | Error, % |
| Vertical displacement Z (point Â), m | -0,01 | -0,01 | 0 |
| Vertical reaction H (point B), N: | -21000 | -21000 | 0 |
| Bending moment M (point B), kN*m | 63000 | 63000 | 0 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.


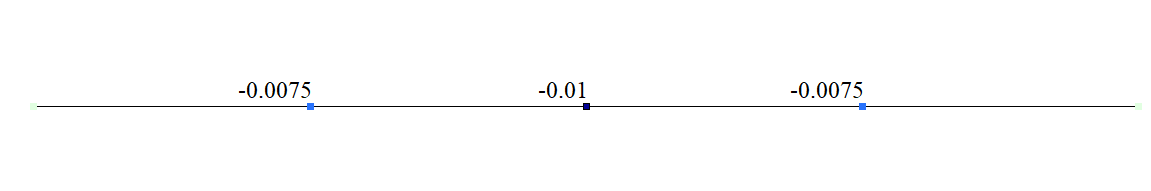
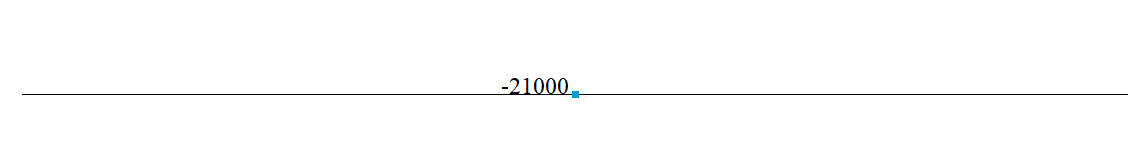

Comments