Objective
To determine the stress state in the elements of a spatial pin-jointed bar system subjected to a concentrated load.
Reference
F. P. Beer, E. R. Johnston Jr., D. F. Mazurek, P. J. Cornwell, E. R. Eisenberg, Vector Mechanics for Engineers, Statics and Dynamics, New York, McGraw-Hill Co., 1962, p. 47.
Problem statement
To determine the axial forces N in each bar.
Design model
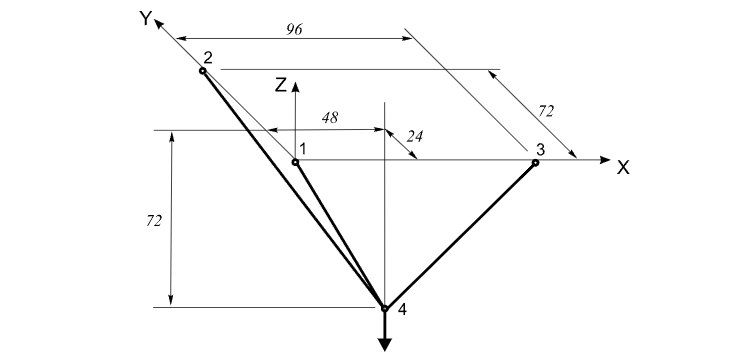
Three bars of a spatial system are connected at a common joint (node 4) and are pin-supported at the opposite joints (nodes 1, 2 and 3).
|
|
|
|
Initial geometry of analytical model
|
Initial geometry of FE model
|
Geometry
Cross-sectional area of bars ААС = 1,0 m2
Material properties
Modulus of elasticity Е = 3,0 * 107 Pa.
Loads
Vertical concentrated load: F = 0,05 kN.
Note
The design model is a spatial pin-jointed bar system with three bar elements of type 4.
Boundary conditions at the support nodes are imposed by restraining the X, Y, and Z degrees of freedom. Number of nodes in design model: 4.
Output data
|
|
|
|
Design and deformed shape of a truss
|
Diagram of axial forces, N (N)
|
Analytical solution
In the analytical solution, the axial forces N in the elements of the spatial pin-jointed bar system under a vertical concentrated load are obtained from the following formulas:
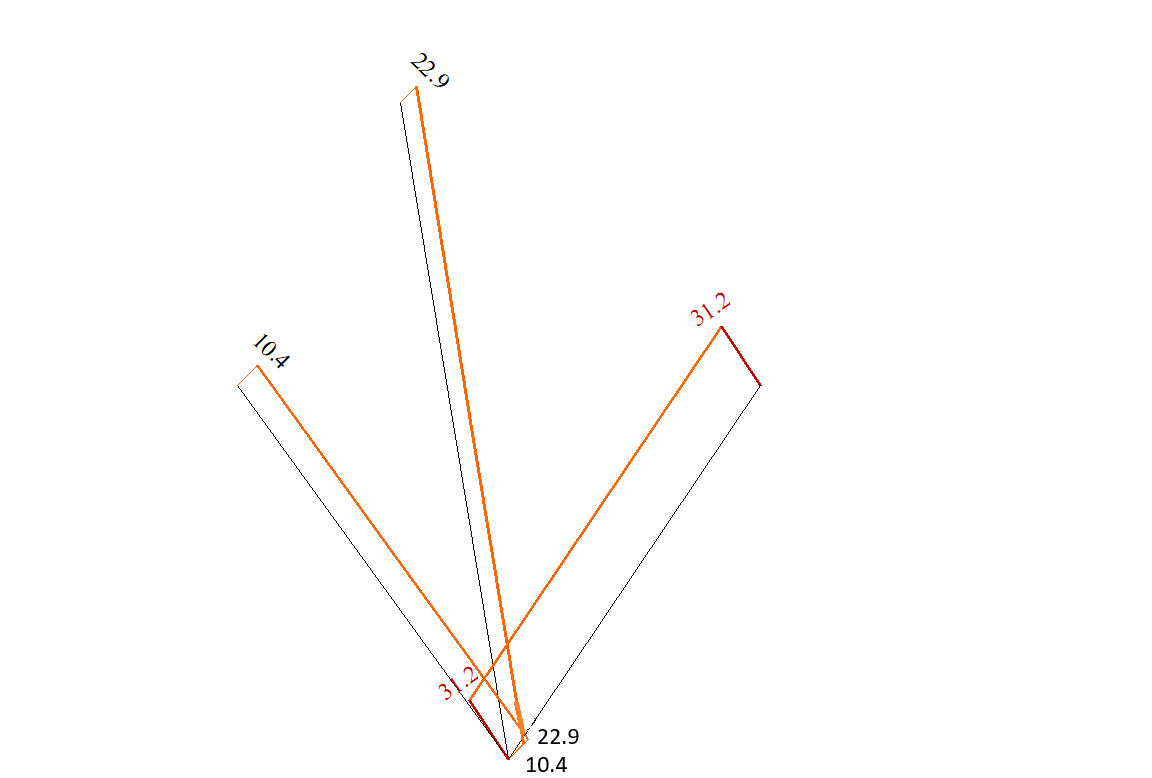
Comparison of calculation results
Values of axial forces, N (N)
| Bar(nodes) | Analytical solution | LIRA-FEM | Error, % |
| 1 (1-4) | 10,39 | 10,4 | 0,1 |
| 2 (2-4) | 22,91 | 22,9 | 0,04 |
| 3 (3-4) | 31,18 | 31,2 | 0,06 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.
Comments