Objective
To determine the stress–strain state of a system of intersected bars subjected to a distributed load and a concentrated load acting in the plane of the system.
Reference
S. Timoshenko et D.H. Young, Theorie des constructions, Paris, Librairie Polytechnique Beranger, 1949, p. 412-416.
Problem statement
To determine the horizontal (X) and vertical (Z) displacements of the common joints of the first (point C) and second (point D) pairs of bars of the system.
Design model
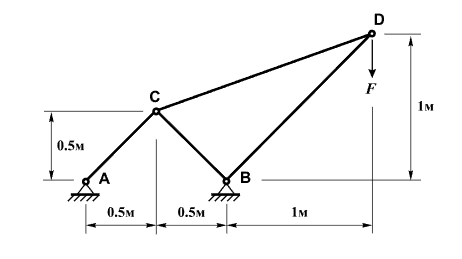
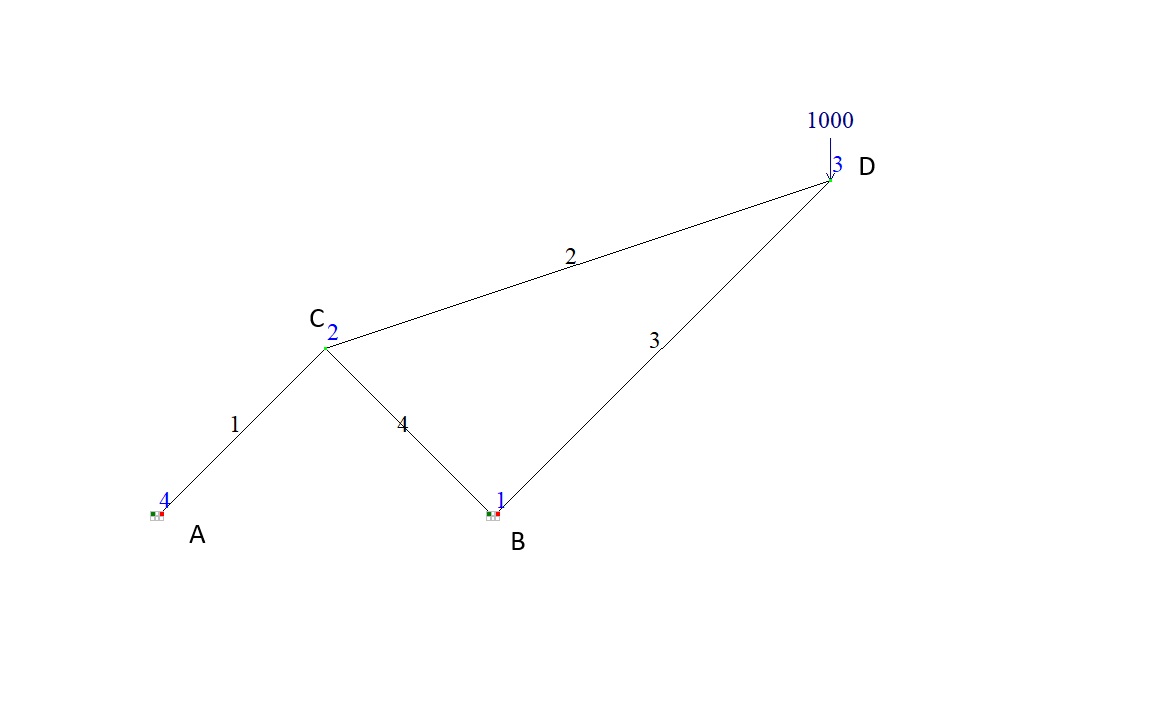
The plane pin-jointed bar system consists of four inclined bars.
In the first pair, the bars have equal lengths and identical cross-sectional stiffnesses, are connected to a common node (point C), and are pin-supported at the opposite nodes (points A and B).
In the second pair, the bars have identical cross-sectional stiffnesses, are connected to a common node (point D), and are connected at the opposite nodes (points C and B) to one of the bars of the first pair.
A vertical concentrated load F is applied at the common joint of the second pair of bars.
|
|
|
|
Initial geometry of analytical model
|
Initial geometry of FE model
|
Geometry
Coordinate of node A: XА = 0,0 m;YА = 0,0 m;
Coordinate of node A: XB = 1,0 m;YB = 0,0 m;
Coordinate of node A: XC = 0,5 m;YC = 0,5 m;
Coordinate of node A: XD = 2,0 m;YD = 1,0 m;
Cross-sectional area of the bar AC ААС = 2,0 * 10-4 m2;
Cross-sectional area of the bar BC АBC = 2,0 * 10-4 m2;
Cross-sectional area of the bar CD АCD = 1,0 * 10-4 m2;
Cross-sectional area of the bar BD АBD = 1,0 * 10-4 m2;
Material properties
Modulus of elasticity Е = 2,0 * 1010 Pa.
Loads
Vertical concentrated load: F = 1 kN.
Note
The structural model is a plane pin-jointed bar system consisting of four bar elements FE type 10.
The boundary conditions are defined by restraints applied in the X and Z directions at the pinned support nodes (points A and B).
Number of nodes in design model: 4.
Output data
|
|
|
|
|
Design and deformed model of the truss
|
Horizontal displacements X (m)
|
Vertical displacements Z (m)
|
Comparison of calculation results
| Parameters | Analytical solution | LIRA-FEM | Error, % |
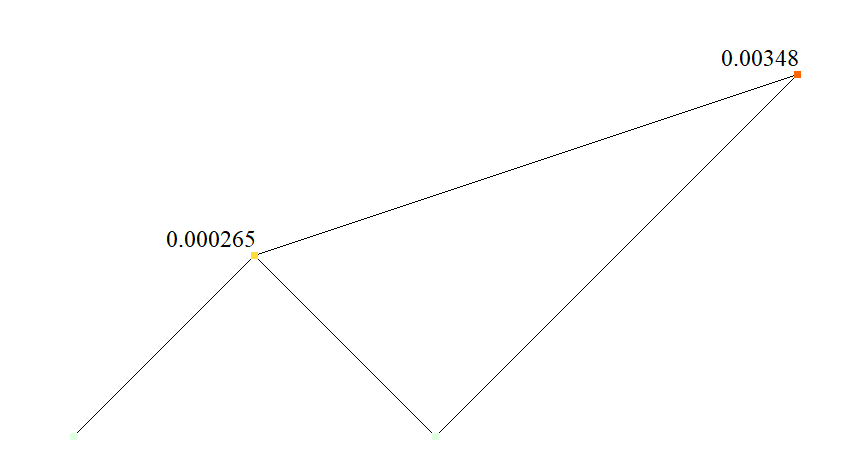
| Horizontal displacement X (point C), m | 2,6517 * 10-4 | 2,6517 * 10-4 | 0 |
| Vertical displacement Z (point C), m | 0,8839 * 10-4 | 0,8839 * 10-4 | 0 |
| Vertical displacement X (point D), m | 34,7903 * 10-4 | 34,7904 * 10-4 | 0,00026 |
| Vertical displacement Z (point D), m | -56,0035 * 10-4 | -56,0037 * 10-4 | 0,00036 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.
Comments