Objective
To determine the stress–strain state of a plane truss under mechanical, thermal and kinematic loads.
Reference
M. Laredo, Résistance des matériaux, Paris, Dunod, 1970, P. 579.
Problem statement
Determine the axial force in the diagonal element at support BD and the vertical displacement v at point D.
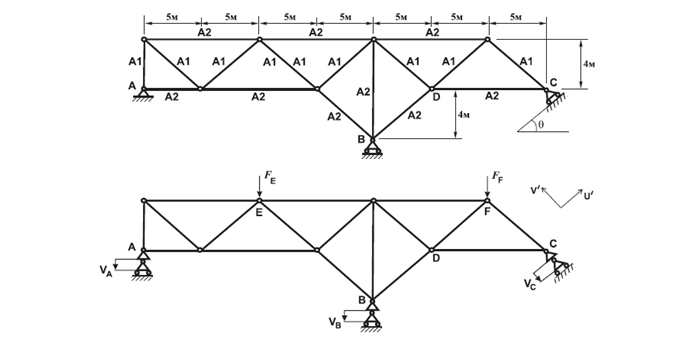
Design model
The two-span truss is subjected to:
-
two concentrated loads FE and FF applied at the nodes of the top chord,
-
uniform heating of all cross-sections of the elements by ΔT,
-
displacements of its supports by VA, VB and VC.
Geometry
The inclination angle of the support zone at node C relative to the horizontal is θ = 30°.
Cross-sectional areas of the bars À1 = 1,41 * 10-3 m2; À2 = 2,82 * 10-3 m2.
Material properties
Modulus of elasticity Å = 2,1 * 1011 Pa.
Coefficient of thermal expansion α = 10-5 C-1.
Boundary conditions
In both linear and nonlinear analyses, no restraint is imposed in the direction of a prescribed displacement. Since all loads are applied within a single load case, the model is restrained only at node A against displacement along the global X-axis (X(uA) = 0).
Loads
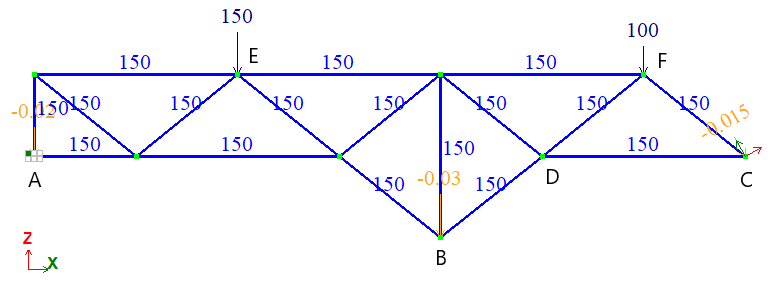
Forced displacements: VA = -0,02 m; VÂ = -0,03 m; VC = -0,015 m.
Vertical concentrated loads: FE = 150 kN; FF = 100 kN.
Thermal load: all bars are heated to a temperature of 150°C.
Note
The problem is solved in a plane formulation (model type 1 – XOZ plane).
The model is generated with FE type 1 – FE of 2D truss. Since the nodes of FE type 1 have two degrees of freedom – translations along the global X and Z axes – the connections between these elements at the nodes are pinned.
A local coordinate system is assigned to the node at point C, with the X1-axis aligned with the direction of the load applied at this node.
Number of nodes: 10. Number of elements: 17.
Output data
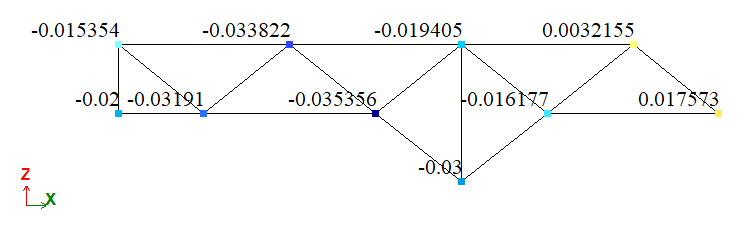
Comparison of calculation results
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % |
| D | Displacement VD, m | -0,01618 | -0,016177 | 0,0185 |
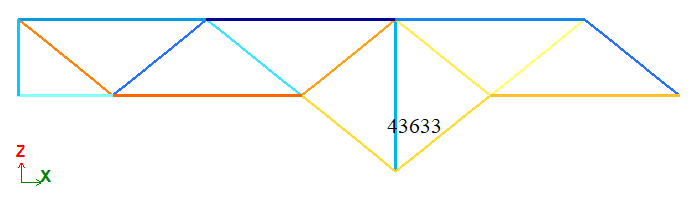
| BD | Axial force, N | 43633 | 43633 | 0 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.
Comments