Objective
To determine the stress–strain state of a vertical prism subjected to loading due to its self-weight.
Reference
S. P. Timoshenko, J. N. Goodier. Theory of Elasticity, M., Nauka, 1975, pp. 289–291.
Problem statement
To determine the vertical displacements Z (w) at points B and C, the horizontal displacement X (u) at point D, as well as the stresses near the upper face and at mid-height of the bar.
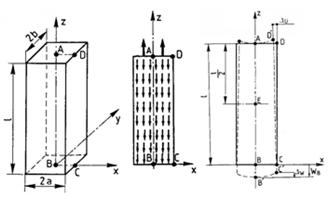
Design model
A vertical prism subjected to its self-weight and to a load applied at the upper face, equal to the weight of the bar.
|
Variant 1 |
Variant 2 |
Geometry
Length L = 3 m
Dimensions of cross-section a = b = 0,5 m
Material properties
Modulus of elasticity Å = 2 * 107 tf/m2
Poisson's ratio ν = 0,3
Unit weight R0 (ρg) = 7,8 tf/m3
Boundary conditions
Point A is restrained in the Z direction (Z (w_A) = 0) to prevent geometric instability.
Restraints are applied in the Y direction (v = 0) on the XZ cut plane, and in the X direction (u = 0) on the YZ cut plane.
Loads
Self-weight acting on the prism (downwards).
A uniformly distributed load (equal in total value to the unit weight of the prism) is applied to the upper face of the prism (acting upwards).
Note
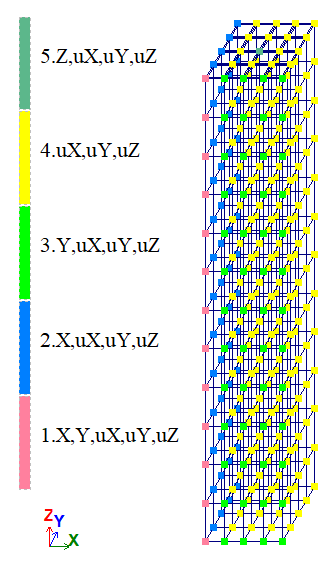
The problem is solved in a 3D formulation (model type 5).
The model is generated with FE type 31 – parallelepiped.
Only one quarter of the prism is considered in the design model; symmetry restraints are applied on the cut planes.
To apply the load to the upper face of the prism, FE type 11 plate elements with E = 0 and ν = 0 are used.
Variant 1:
FE mesh 4×4×12.
Number of nodes: 325. Number of elements: 208.
Variant 2:
FE mesh 8×8×24.
Number of nodes: 2025. Number of elements: 1600.
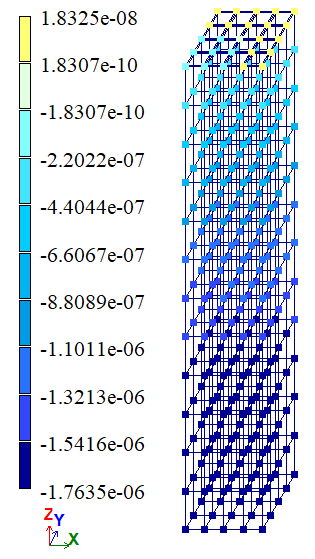
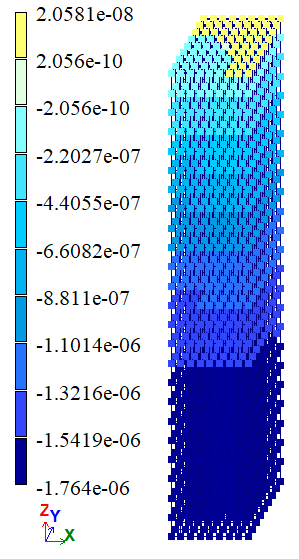
Output data
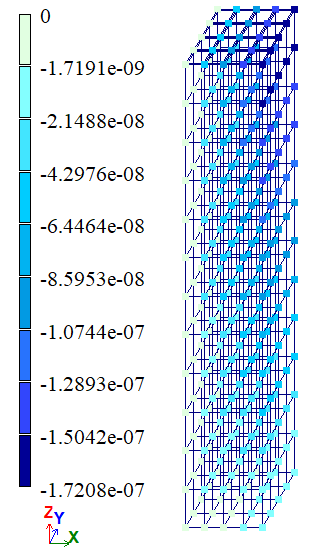
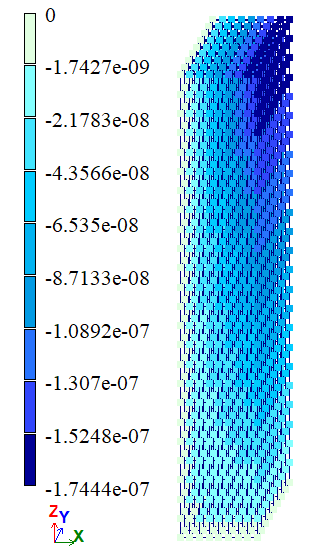
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
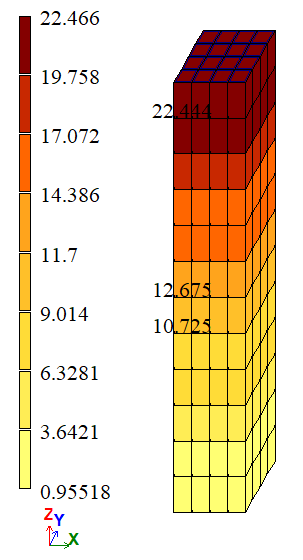
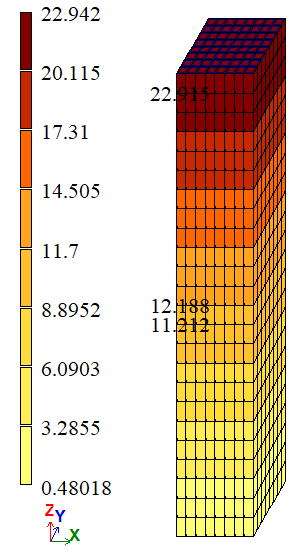
|
Variant 1 |
Variant 2 |
Analytical solution
σzz = ρgz
σxx = σyy = σxy = σyx = σzx = 0
u = -νρgxz/E

Comparison of calculation results
Without additional side nodes:
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % | ||
| Variant 1 | Variant 2 | Variant 1 | Variant 2 | |||
| Â | w (Δz), m | -1,755*106 | -1,755*106 | -1,755*106 | 0 | 0 |
| Ñ | w (Δz), m | -1,74*106 | -1,7584*106 | -1,7447*106 | 1,0464 | 0,2694 |
| D | u (Δx), m | -1,755*107 | -1,7182*107 | -1,7418*107 | 2,0969 | 0,7521 |
| À | σZZ, tf/m2 | 23,4 | 22,444 | 22,9148 | 4,0855 | 2,0735 |
| Å | σZZ, tf/m2 | 11,7 | 11,7 | 11,7 | 0 | 0 |
With additional side nodes:
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % | ||
| Variant 1 | Variant 2 | Variant 1 | Variant 2 | |||
| Â | w (Δz), m | -1,755*106 | -1,7547*106 | -1,7549*106 | 0,0171 | 0,0057 |
| Ñ | w (Δz), m | -1,74*106 | -1,7437*106 | -1,7439*106 | 0,2122 | 0,2236 |
| D | u (Δx), m | -1,755*107 | -1,7533*107 | -1,7545*107 | 0,0969 | 0,0285 |
| À | σZZ, tf/m2 | 23,4 | 22,444 | 22,9226 | 4,0855 | 2,0402 |
| Å | σZZ, tf/m2 | 11,7 | 11,7 | 11,7 | 0 | 0 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.

Comments