Objective
To determine the stress–strain state of a prismatic beam subjected to a bending moment.
Reference
S. Timoshenko, Théorie de l’élasticité, Paris, Librairie Polytechnique Ch. Béranger, 1961, P. 284-289.
Problem statement
To determine the displacement in the X direction at point A, in the Z direction at point B, and in the Y direction at points D, E, F, and G.
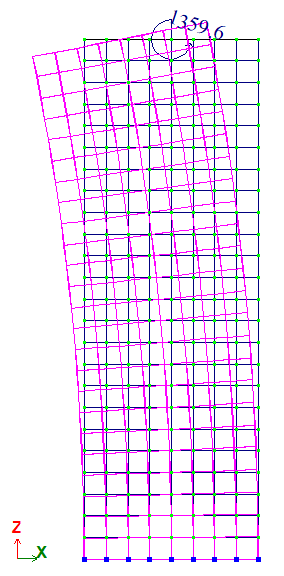
Design model
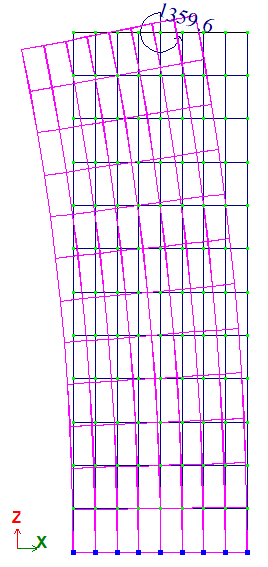
A cantilever prismatic beam subjected to a bending moment applied at the free end.
|
Variant 1 |
Variant 2 |
Geometry
Length l = 6 m
Dimensions of a cross-section a = b = 1 m
Ordinate of the control section l′ = (2/3)l = 4 m
Material properties
Modulus of elasticity Å = 2 * 105 MPa
Poisson's ratio ν = 0,3.
Boundary conditions
Restraints in all displacement directions at point B (X=Y=Z=0).
On the plane passing through point B, restraints preventing displacement in the Z direction are applied, together with symmetry restraints.
Loads
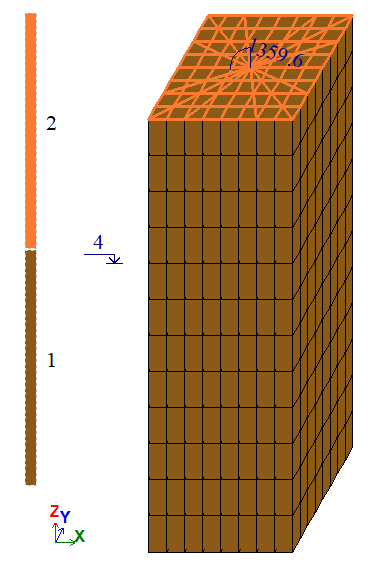
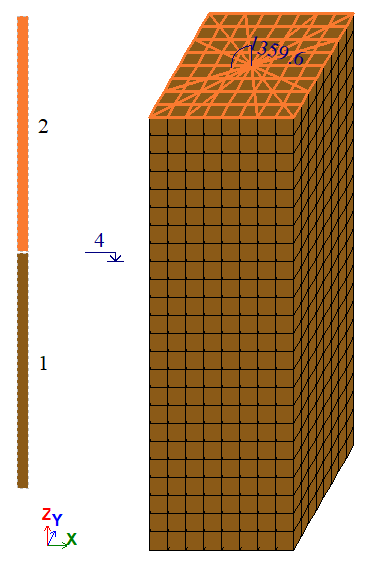
A moment about the Y axis is applied at point C: My = 4/3 * 107 N*m = 1359,62 t*m.
Note
The problem is solved in a 3D formulation (model type 5).
The model is generated with FE type 31 – parallelepiped.
The entire prism is considered in the design model.
A 'spider' made of FE type 10 bar elements was introduced to apply the bending moment to the end face of the prism. This spider simulates a perfectly rigid body (PRB) end face of the prism the end-face plane while maintaining zero stiffness within the plane so as not to restrain transverse deformations. In other words, the bending stiffness assigned out of the cross-section plane is very high, while the axial and bending stiffnesses assigned in the plane of the cross-section are zero.
Variant 1:
FE mesh 8×8×12.
Number of nodes: 1053. Number of elements: 944.
Variant 2:
FE mesh 8×8×24.
Number of nodes: 2025. Number of elements: 1712.
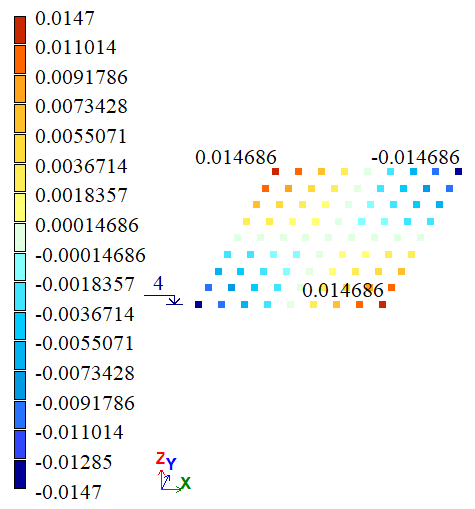
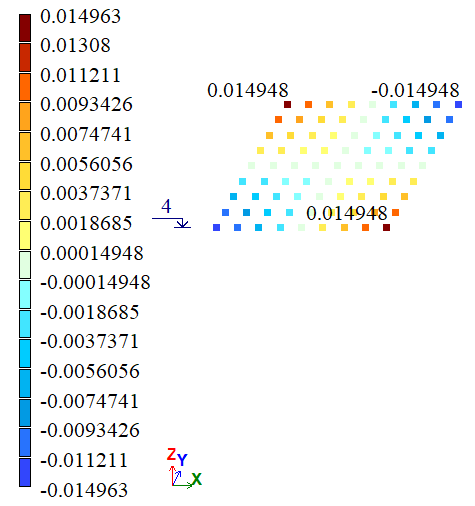
Output data
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
|
Variant 1 |
Variant 2 |
Analytical solution
σxx = σyy = σxy = σyx = σzx = 0
u = -l’2/2R
w = l’2/R
v = ν(a2/R)
Comparison of calculation results
| Point | The unknown | Analytical solution | LIRA-FEM | Error, % | ||
| Variant 1 | Variant 2 | Variant 1 | Variant 2 | |||
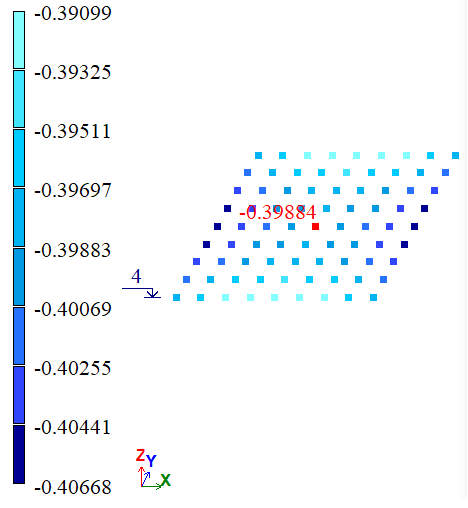
| À | Õ, m | -4*10-4 | -3,9174*10-4 | -3,9884*10-4 | 2,065 | 0,29 |
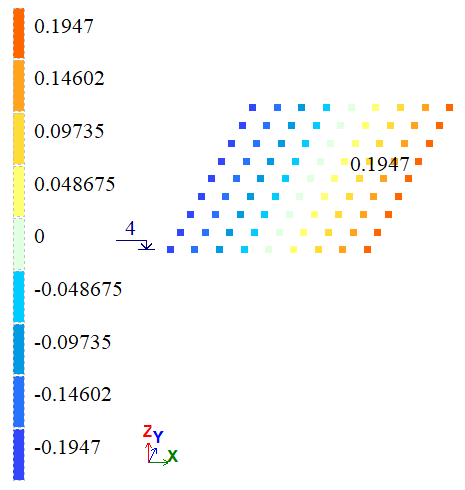
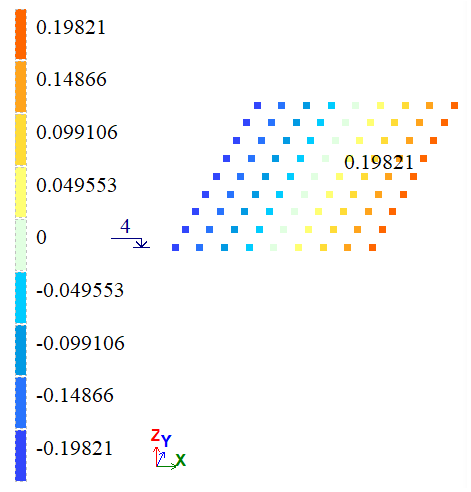
| À | Õ, m | 2*10-4 | 1,947*10-4 | 1,9821*10-4 | 2,65 | 0,895 |
| F, G, D, E | Y, m | 0,15*10-4 | 0,14686*10-4 | 0,14948*10-4 | 2,0933 | 0,3467 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.

Comments