Objective
To determine the stress–strain state of a 3D bar system with elastic restraints subjected to a concentrated load.
Reference
M. Laredo, Résistance des matériaux, Paris, Dunod, 1970, P. 165.
Problem statement
Determine:
-
the vertical displacement Z at the joint of bars AD and HD (point D);
-
the horizontal displacement and rotation at point A;
-
the torsional and bending moments Mx, My, Mz at the support nodes of the 3D system (points A and B).
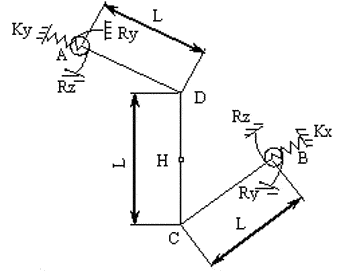
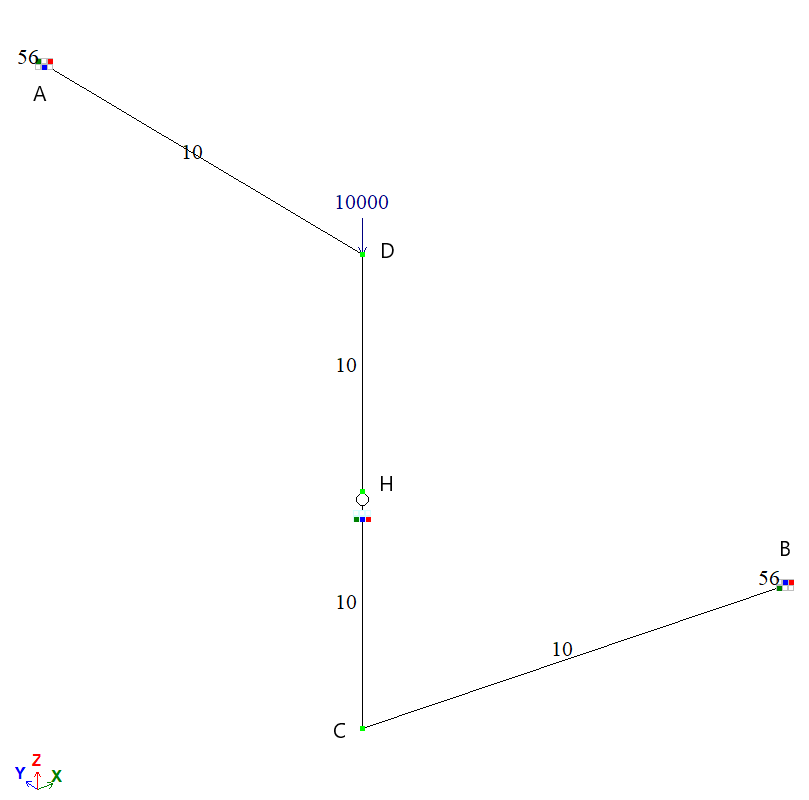
Design model
The 3D model consists of four bars. The horizontal bars lie orthogonally in two parallel horizontal planes and are connected by vertical bars that are hinged to each other (point H).
At the support nodes of the 3D model (points A and B), rigid restraints are provided for translational and rotational degrees of freedom (DOF) in the plane of the cross-section, and elastic restraints are provided for translational and rotational DOF out of the plane of the cross-section.
At the joint of the upper horizontal bar and the vertical bar (point D) a vertical concentrated load F is applied.
|
|
|
|
a |
b |
Geometry
Length of horizontal bars L = 2 m;
Length of vertical bars 0,5L = 1 m;
Moments of inertia for a cross-section Iy = Ix = I = 10-6 m4;
Polar moment of inertia (torsional constant) J = 2 * 10-6 m4;
Cross-sectional area A = 0,001 m2.
Material properties
Modulus of elasticity Е = 2,1 * 1011 Pa;
Shear modulus G = 7,875 * 1010 Pa.
Boundary conditions
At point A:
- rigid restraints for the degrees of freedom uY (θY=0), X and Z (uA=wA=0);
- elastic restraints for degrees of freedom Y, uX, uZ:
Rу = 52500 N/m, Rux = Ruz = 52500 N*m/rad.
At point B:
- rigid restraints for the degrees of freedom uX (θX=0), Y and Z (uB=wB=0);
- elastic restraints for degrees of freedom X, uY, uZ:
Rх = 52500 Н/м, Ruy = Ruz = 52500 Н*м/рад.
At point Н: hinge.
Loads
Vertical concentrated load F = 10000 Н applied at point D.
Note
The problem is solved in 3D formulation (model type 5).
The FE type 10 (arbitrary 3D bar) are applied to generate the model.
Elastic restraints at points A and B are defined with FE type 56 (1-node FE of elastic springs).
At point H of bar CD, a hinge is introduced for degrees of freedom uY, uX, uZ.
Number of nodes: 5.
Number of elements: 6.
Output data
|
|
|
|
|
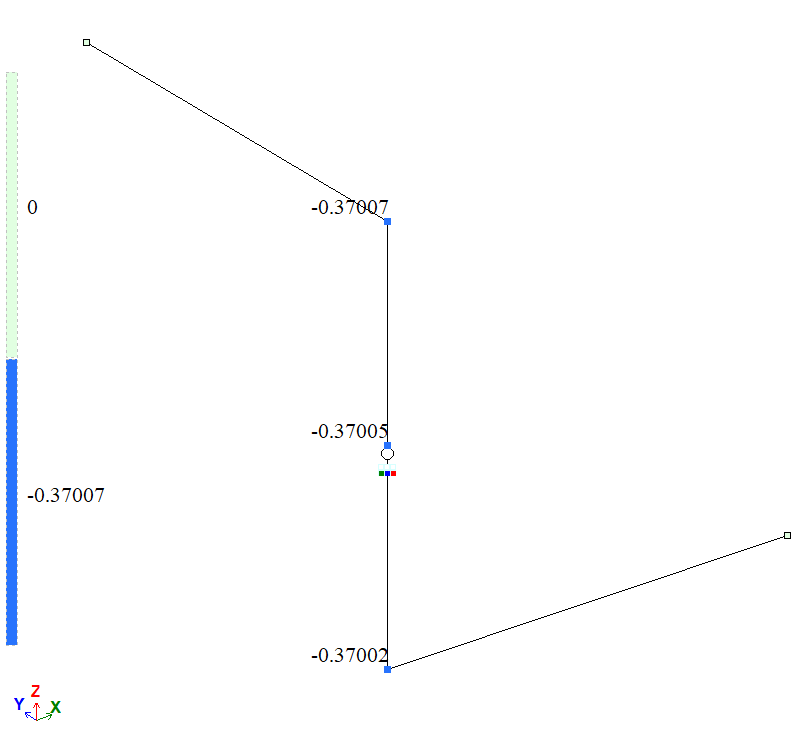
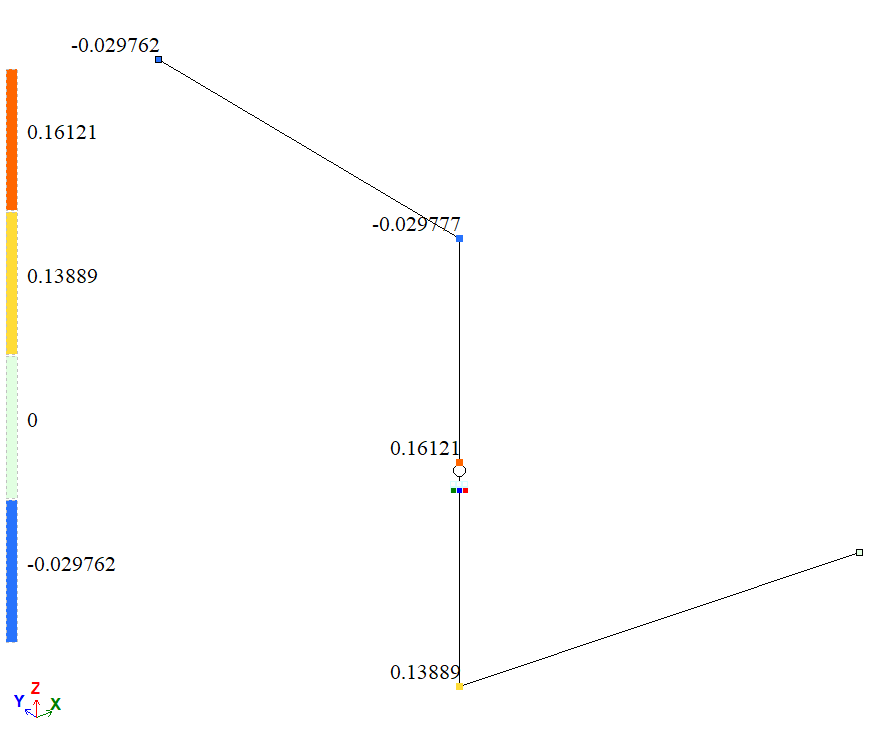
Mosaic plot of vertical displacements along the global Z-axis (w), m |
Mosaic plot of horizontal displacements along the global Y-axis (v), m |
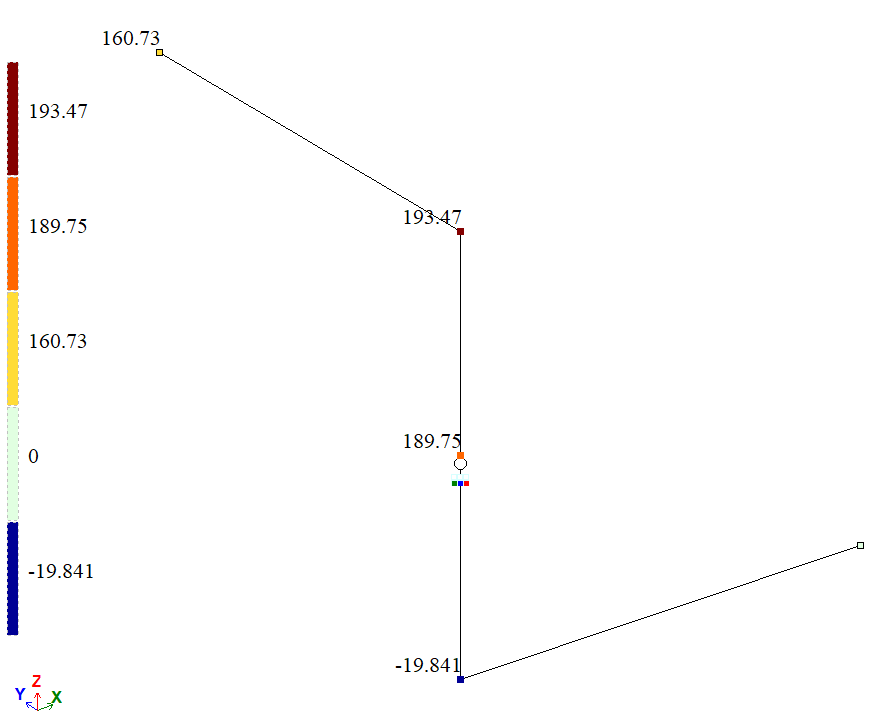
Mosaic plot of rotation angles about the global X-axis (u), rad*1000 |
|
|
|
|
|
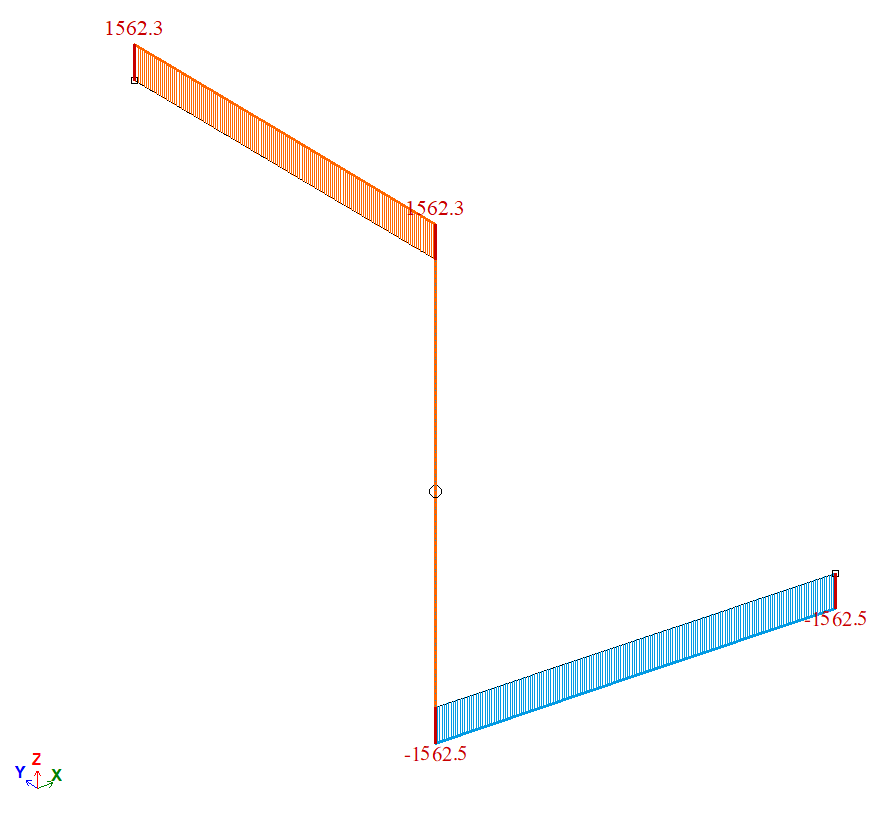
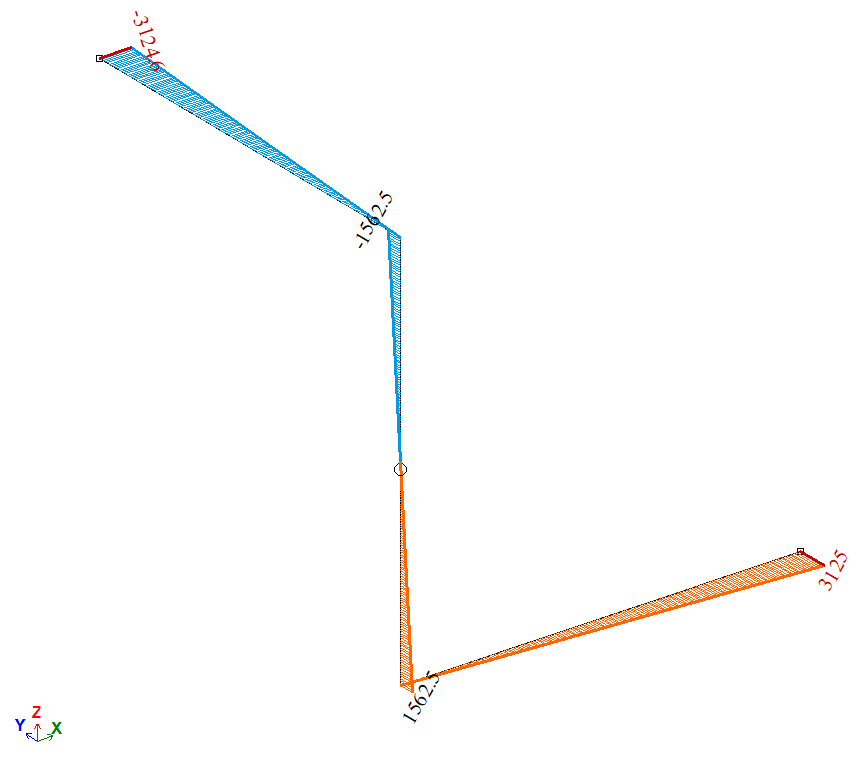
Diagram of twisting moments Мх, N*m
|
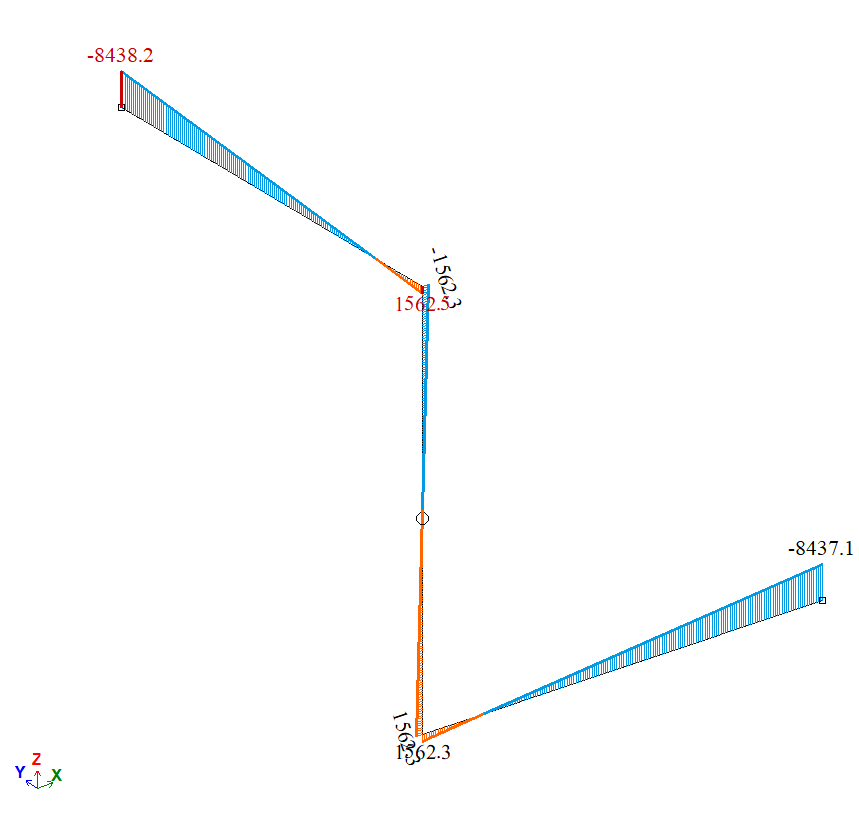
Diagram of bending moments My, N*m
|
Diagram of bending moments Мz, N*m
|
Analytic solution
MAx = 5*F*l/64
MAy = 27*F*l/64
MAz = -5*F*l/32
MBx = -27*F*l/64
MBy = -5*F*l/64
MBz = -5*F*l/32
νA = 5*F*l/(64*EI)
θAx = -27*F*l2/(32*EI)
ωD = 373*F*l3/(384*EI)
Comparison of calculation results
| Point | The unknown | Analytic solution | LIRA-FEM | Error, % |
| А | Moment Мх, N*m | 1562,5 | 1562,3 | 0,0128 |
| А | Moment Му, N*m | 8437,5 | 8438,2 | 0,083 |
| А | Moment Мz, N*m | 3125 | 3124,6 | 0,0128 |
| B | Moment Мх, N*m | 1562,5 | 1562,5 | 0 |
| B | Moment Му, N*m | 8437,5 | 8437,1 | 0,0047 |
| B | Moment Мz, N*m | 3125 | 3125 | 0 |
| А | Displacement νA, m | 0,02976 | 0,02977 | 0,001 |
| А | Rotation angle θAX, rad | 0,16071 | 0,16073 | 0 |
| D | Displacement ωD, m | 0,37004 | 0,37007 | 0,0027 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.
Comments