Врахування нелінійної роботи залізобетону в ПК ЛІРА-САПР. Метод «Інженерна нелінійність»

У статті розглядається ітераційний метод «інженерна нелінійність». Пропонований метод дозволяє визначити реальні жорсткістні характеристики перерізу, які можуть бути зниженими у зв'язку з появою тріщин, пластичними деформаціями бетону та арматури.

Пропонований метод «інженерна нелінійність», з одного боку, дозволяє більш точно враховувати розподіл жорсткостей, з іншого боку по технології практично аналогічний традиційним методам розрахунку в лінійній постановці, тобто дозволяє виконати розрахунок на всі навантаження, отримати РСЗ та РСН, підбір арматури.

Постановка задачі

Повзучість, тріщини та інші специфічні особливості залізобетону зумовлюють зміну жорсткістних характеристик елементів на ранніх етапах навантаження, включаючи і експлуатаційну стадію. Це призводить до перерозподілу зусиль, значного збільшення переміщень порівняно з лінійно-пружним розрахунком. Нормативні документи орієнтують інженера на врахування цих факторів. Так у Єврокоді та нормативах Російської Федерації рекомендується проводити розрахунок з урахуванням фізичної нелінійності. Програмний комплекс ЛІРА-САПР надає можливість інженеру виконувати такі розрахунки. Однак розрахунок конструкції з урахуванням фізичної нелінійності [2, 3, 6] у строгому математичному розумінні цього процесу при використанні в масових інженерних розрахунках має низку недоліків:

• такий розрахунок може бути виконаний тільки на одне навантаження та його не можна використовувати в РСЗ або РСН;
• такий розрахунок потребує великих ресурсовитрат – кроковий метод обумовлює необхідність багаторазового вирішення систем лінеаризованих рівнянь;
• такий розрахунок вимагає завдання арматури (діаметри та розташування) у кожному перерізі стержня або пластинчастого елемента.

З іншого боку, нормативи Російської Федерації СП 52-103-2007, для врахування цих факторів в інженерних розрахунках, пропонують просто вводити понижуючі коефіцієнти на жорсткість 0,3 - для елементів, що згинаються, і 0,6 - для елементів, що стискаються. Звичайно, таке грубе припущення не враховує, що зниження жорсткості залежить від величини та характеру напружено-деформованого стану перерізу. Про зниження жорсткості розтягнутих елементів взагалі нічого не йдеться.

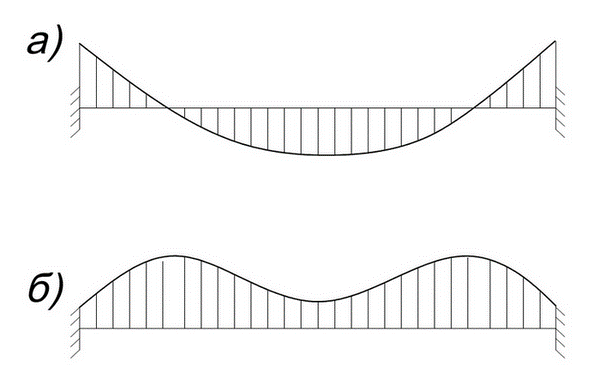
Такий підхід досить грубо оцінює дійсну ситуацію. Це можна продемонструвати на прикладі елементарної защемленої балки (рис.1).

У реальних розрахунках ситуація ще складніша. Колони часто відчувають значні нормальні зусилля: балки зазнають значних згинальних зусиль; у пластичних елементах, як правило, виникають сумірні мембранні та згинальні зусилля.

Метод «Інженерна нелінійність» орієнтовано деяке усунення цієї невідповідності (деякі ідеї у цьому напрямку пропонувалися раніше [1]) і цей метод треба позиціонувати як метод уточненого диференційованого врахування зниження жорсткістних характеристик залізобетонних елементів.

Концепция метода

Метод «Інженерна нелінійність» полягає в наступному:

1. Задається "визначальне навантаження", яке на думку інженера в основному визначає напружено-деформований стан конструкції (розвиток тріщин, пластичні деформації бетону та арматури) протягом життєвого циклу конструкції. «Визначальне навантаження» може складатися на основі набору навантажень (власна вага, корисні навантаження та ін.), які задаються інженером для наступного традиційного розрахунку або призначається інженером на основі інших припущень.
2. Розраховується на «визначальне навантаження» у фізично нелінійній постановці з одночасним підбором арматури. Розрахунок виконується ітераційним методом та проводиться підбір арматури.
3. У результаті ітераційного розрахунку на основі НДС кожного перерізу стержня та КЕ пластинчастої конструкції визначаються жорсткістні характеристики.
4. Виконується традиційний розрахунок конструкції, елементи якої мають жорсткістні характеристики, які визначаються в результаті ітераційного розрахунку. Традиційний розрахунок передбачає розрахунок у лінійно-пружній постановці на весь набір навантажень (власна вага, корисне навантаження, сейсміка та ін.), складання РСЗ або РСН, підбір чи перевірку перерізів стержнів залізобетонних та сталевих елементів, конструювання.

Найбільш відповідальним і складним у постановці та реалізації є етап визначення жорсткістних характеристик перерізів стержня та пластинчастого елементу [4,5].

Визначення жорсткістних характеристик перерізу стержня

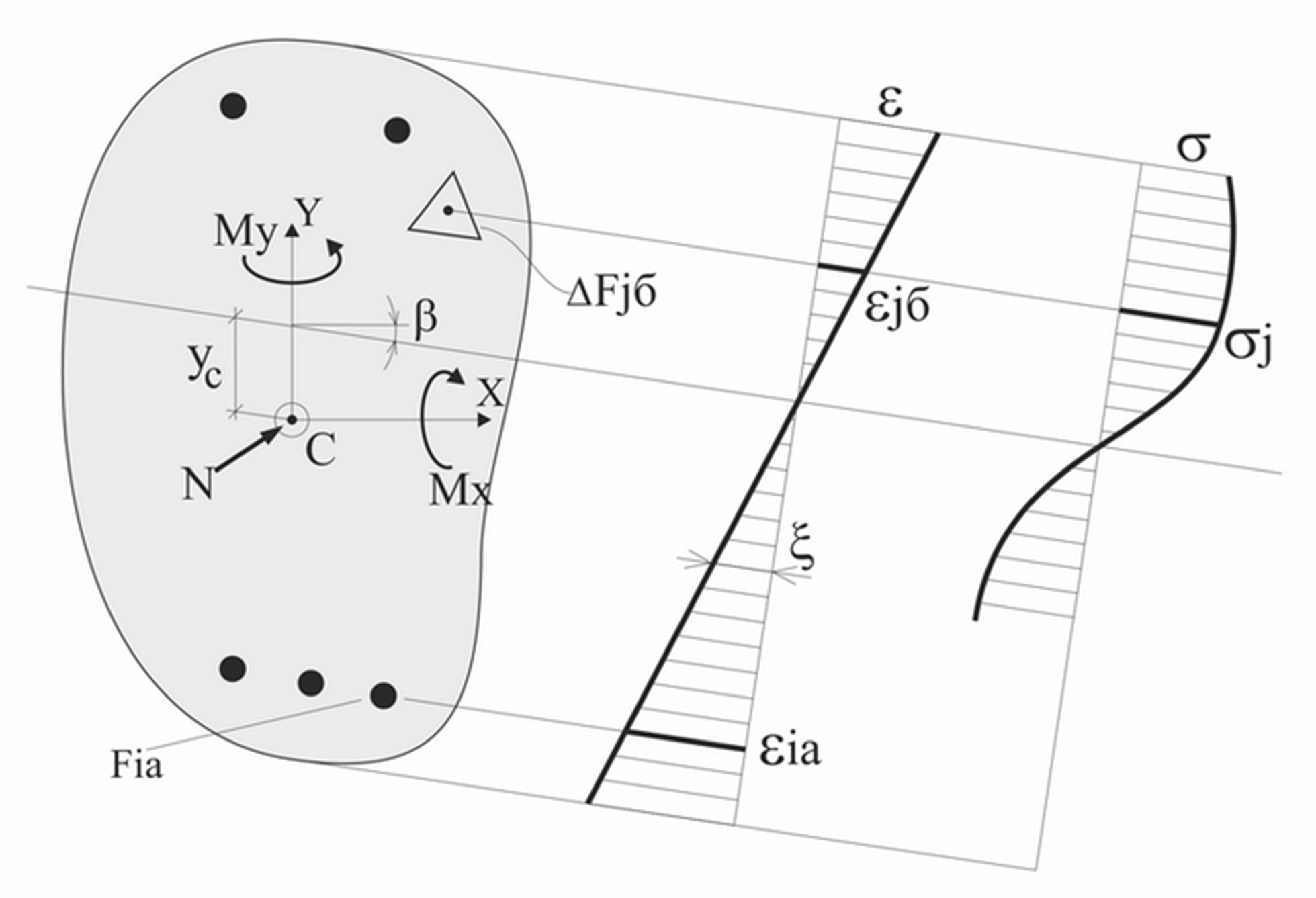
На рис. 2 представлений довільний переріз стержня, на який діє два моменти Mx та My, нормальна сила N. Моменти діють відносно головних осей перерізу x та y. Нормальна сила прикладена у точці С – перетинанні геометричної осі стержня з площиною перерізу. Потрібно: визначити жорсткістні характеристики перерізу, що відповідають модулям деформацій бетону та арматури.

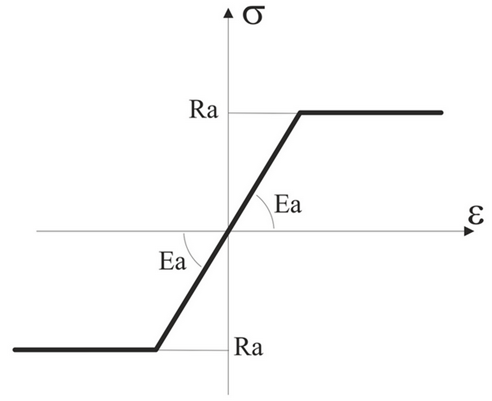
Залежність  ддля бетону представлено на рис. 3, для арматури – на рис. 4.

Для визначення НДС перерізу необхідно знайти положення нейтральної осі, яке характеризується двома величинами ,  та кривизною перерізу  (рис.2):
– зсув нейтральної осі;
  – кут повороту нейтральної осі;
  – кривизна перерізу.
Розв'язання задачі виконується чисельним методом. В результаті ітераційного процесу визначаються три невідомі , , , які знаходяться із трьох рівнянь рівноваги: 

Тут – елементарні ділянки, на які розчленовується переріз бетону та площі окремих стержнів арматури.

n – кількість ділянок бетону, m – кількість арматурних стержнів.

 

– січні модулі деформацій бетону та арматури, які визначаються на основі залежностей  (рис. 2,3).

Х_jб, Y_jб, X_ia, Y_ia – відстань центру тяжкості j-ї ділянки бетону та i-ї ділянки арматурного стержня до головних осей, положення яких (, ) визначено у результаті ітераційного розрахунку.

Для бетону у визначення входить лише стиснута частина бетону зі змінним по перерізу січним модулем деформації. Для кожного арматурного стержня також використовується відповідний січний модуль деформації.

Матриця жорсткості стержня, що має змінні по довжині січні жорсткістні характеристики (рис.1) також будується чисельним методом (кожен стержень розглядається як своєрідний суперелемент).

Приклади застосування

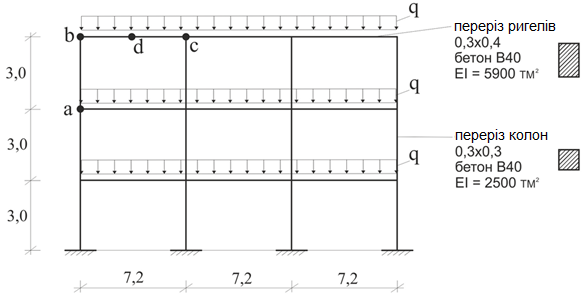
Нижче наводяться результати розрахунку рами на основі інженерної нелінійності (рис. 4).

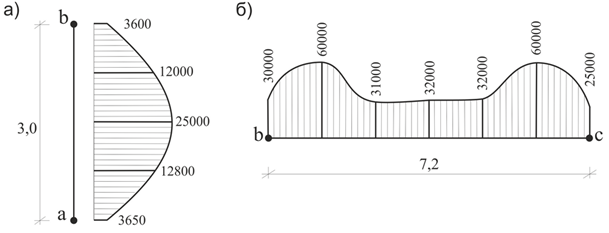
В якості визначального навантаження було прийняте навантаження q=15 т/п.м. на рис. 6 наведені відповідні жорсткості для ригеля b – с та колон а – b.

Аналізуючи епюри жорсткістних характеристик можна зробити висновок, що рекомендоване нормативами зниження жорсткістних характеристик для колон на знижувальний коефіцієнт 0,6 (у цьому випадку епюра для колон виглядала б постійною та рівною 0,6х2500=1500 тм²) і для ригелів 0,3 (у цьому випадку епюра виглядала б постійною та рівною 0,3х5900=1770 тм²) виглядає досить грубим наближенням.

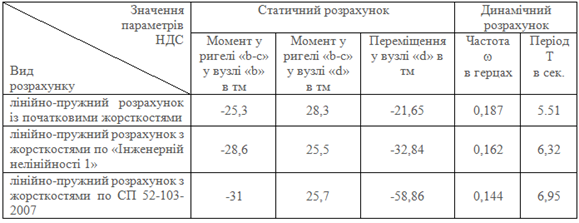
У таблиці 1 наведено результати лінійно-пружного розрахунку рами на навантаження q=20 т/п.м. з урахуванням диференційованого розподілу жорсткостей для всіх елементів, отриманих на основі режиму «Інженерна нелінійність».

Таблиця 1. Результати лінійно-пружного розрахунку рами.

Аналізуючи результати розрахунку наведені у табл. 1 можна зробити наступні висновки:

• отримано деякий перерозподіл зусиль – у менш навантаженому перерізі «b» ригеля момент збільшився, у більш навантаженому перерізі «d» ригеля момент зменшився;
• переміщення вузла «d» збільшилося більш ніж у 2 рази;
• частота власних коливань (перша форма) зменшилася, а період збільшився.

Відображення мозаїк інтегральних жорсткістних характеристик

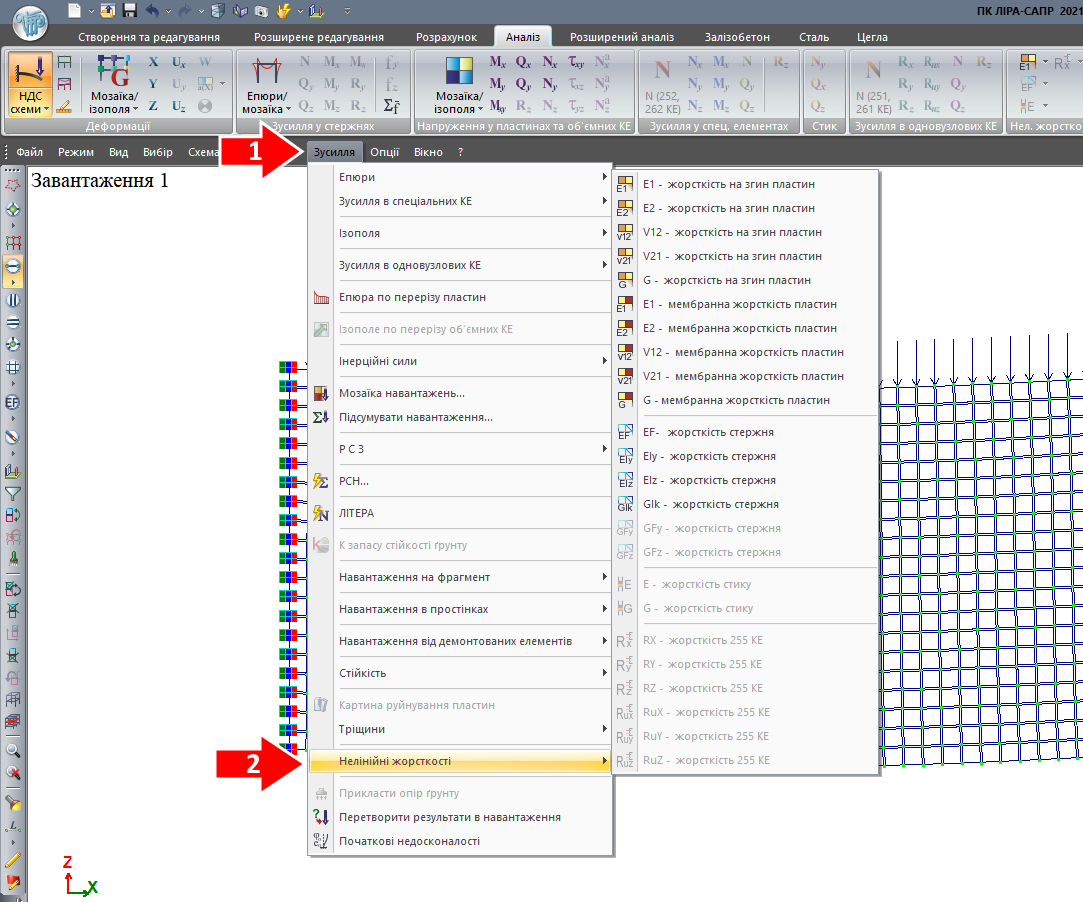
Для розрахунку залізобетонних конструкцій з використанням інженерної нелінійності в ЛІРА-САПР введено побудову мозаїк інтегральних жорсткістних характеристик стержнів та пластин. Мозаїки інтегральних жорсткостей можна включити з меню «Зусилля» в результатах розрахунку.

Приклад мозаїки інтегральної згинальної жорсткості для пластинчастих елементів: у місцях згинальних моментів близьких до нуля (на шарнірній опорі праворуч та на відстані 1/4 прольоту від опори із защемленням) спостерігається локальне збільшення жорсткості перерізу. В інших місцях плити жорсткість знизилася.

Приклад мозаїки інтегральної згинальної жорсткості для стержневих елементів: зверніть увагу – у місцях, де епюра моментів у ригелі перетинає нуль, спостерігається збільшення згинальної жорсткості, в порівнянні з початковою жорсткістю лінійного перерізу з початковим модулем пружності бетону. Це пов'язано з тим, що при розрахунку інтегральних жорсткостей було враховано конструктивну арматуру, установка якої підвищила жорсткість перерізу.

Як видно на мозаїці – балки та колони постійного перерізу перетворилися на елементи змінної жорсткості.

Де перерізи більше навантажені (виникають тріщини, жорсткості елементарних майданчиків перерізу падають відповідно до заданої діаграми роботи матеріалу), там жорсткість зменшується значніше.

Висновки

На закінчення ще раз слід відмітити, що метод «Інженерна нелінійність» призначений лише для врахування зниженої жорсткості залізобетонних конструкцій у масових інженерних розрахунках і в жодному разі не замінює розрахунок з урахуванням фізичної нелінійності.

Метод «Інженерна нелінійність» реалізований у програмному комплексі ЛІРА-САПР. Таким чином, інженери-проектувальники отримали ще один інструмент, що дозволяє враховувати у практичних розрахунках вплив зниженої жорсткості залізобетонних конструкцій на НДС проектованої споруди. Такий підхід дозволяє виконати більш ефективне армування залізобетонних елементів та отримати наближені до реальних переміщень конструкції. При цьому суттєво скорочується і час завдання вихідних даних для розрахунку, і час самого розрахунку, стосовно крокового фізнелінійного розрахунку. Крім того, «Інженерна нелінійність» доступна у всіх конфігураціях програми, а крокова фізнелінійність лише у комплексах PRO і FULL.

---

В ЛІРА-САПР 2018 розроблений другий варіант інженерної нелінійності. На відміну від розробленої раніше, в «інженерній нелінійності 2» – реалізовані нові підходи.

Концепції	Інженерна нелінійність 1 (колишня версія)	Інженерна нелінійність 2
визначальне навантаження	можна включати довільні навантаження	включаються реальні постійно діючі навантаження
розрахунок на визначальне навантаження	ітераційний	кроковий
завдання арматури	арматура підбирається у процесі ітераційного розрахунку	арматура задається
розрахунок по традиційній схемі	розрахунок виконується на всі навантаження на основі модулів деформації	розрахунок на тимчасові навантаження виконується на основі дотичного модуля деформації, що відповідає останньому кроку крокового розрахунку
врахування фізичної нелінійності в монтажі	відсутнє	можливе
врахування нелінійності в роботі платформних стиків	відсутнє	можливе

Список літератури

1. Бондаренко В. М. Инженерные методы нелинейной теории железобетона / В.М. Бондаренко – М.: Стройиздат, 1982. – 287 с.
2. Барабаш М. С. Компьютерное моделирование процессов жизненного цикла объектов строительства: Монография / Мария Сергеевна Барабаш. – К.: «Сталь», 2014. – 301 с
3. Городецкий А. С. К расчету физически нелинейных плоских рамных систем /А. С. Городецкий, В. С. Здоренко // Строительная механика и расчет сооружений. – 1969. – № 4. – С. 61-68.
4. Пикуль А. В. Определение жесткостных характеристик сечения железобетонного стержня с учетом нелинейных свойств материала / А.В. Пикуль, Д.А. Городецкий // Актуальные проблемы компьютерного моделирования конструкций и сооружений: тезисы докладов IV Международного симпозиума. – Челябинск.: Издательский центр ЮУрГУ, 2012. – С. 228.
5. Городецкий А. С. Учет нелинейной работы железобетонных конструкций в практических расчетах / А. С. Городецкий, М. С. Барабаш // Строительство, материаловедение, машиностроение // Сб. научн. Трудов. – Дн-вск: ПГАСА, 2014. – Вып. 77. – С. 54–59.
6. Городецкий А. С. Компьютерное моделирование процесса нагружения железобетонных конструкций. Сборник научных трудов Луганского национального университета, серия «Технические науки» N49/52, - Л.: Из-во «ЛНАУ», 2004, с.3-10.

• інженерна нелінійність
• фізична нелінійність
• визначальне навантаження
• ітераційний розрахунок
• визначення жорстких характеристик перерізу
• знижена жорсткість залізобетонних конструкцій