Методи чисельного моделювання та розрахунку осідання будівлі

У програмному комплексі «ЛІРА-САПР» є можливість проводити розрахунок основи по різних моделях, в основі яких лежить тривимірна модель ґрунту, побудована на основі інженерно-геологічних досліджень.

Комп'ютерну модель основи можна здійснювати наступними методами:

1. Використання коефіцієнтів жорсткості пружної основи С₁ та С₂.
2. Моделювання ґрунтового масиву через об'ємні CЕ:

• при використанні універсальних просторових КЕ № 34, 36 для опису лінійної деформації ґрунту;
• при використанні фізично нелінійних об'ємних КЕ №271, 272, 273 (при завданні різних варіантів умов міцності).

Найбільш поширеними видами апроксимації роботи неоднорідної основи при статичному розрахунку конструкції є одновузлові, пластинчасті або об'ємні скінченні елементи. При використанні пластинчастих КЕ в ПК «ЛІРА-САПР» реалізовано три методи визначення коефіцієнтів постелі: модель Пастернака, Вінклера-Фусса та модифікований розрахунок моделі Пастернака.

Також, користувач має можливість вибрати схему розрахунку осадки основи (лінійно-деформованого напівпростору або лінійно-деформованого шару).

Розглянемо різні методи моделювання роботи основи на прикладі розрахункової схеми будівлі торговельно-розважального центру.

У першій задачі робота ґрунту моделювалася за допомогою коефіцієнтів постелі, які були розраховані за моделлю Пастернака: С₁=25087.1кН/м³, С₂=4886.04кН/м.

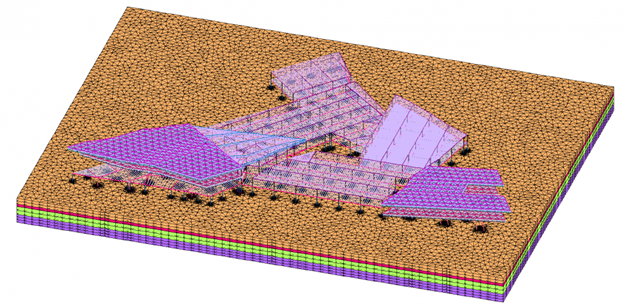
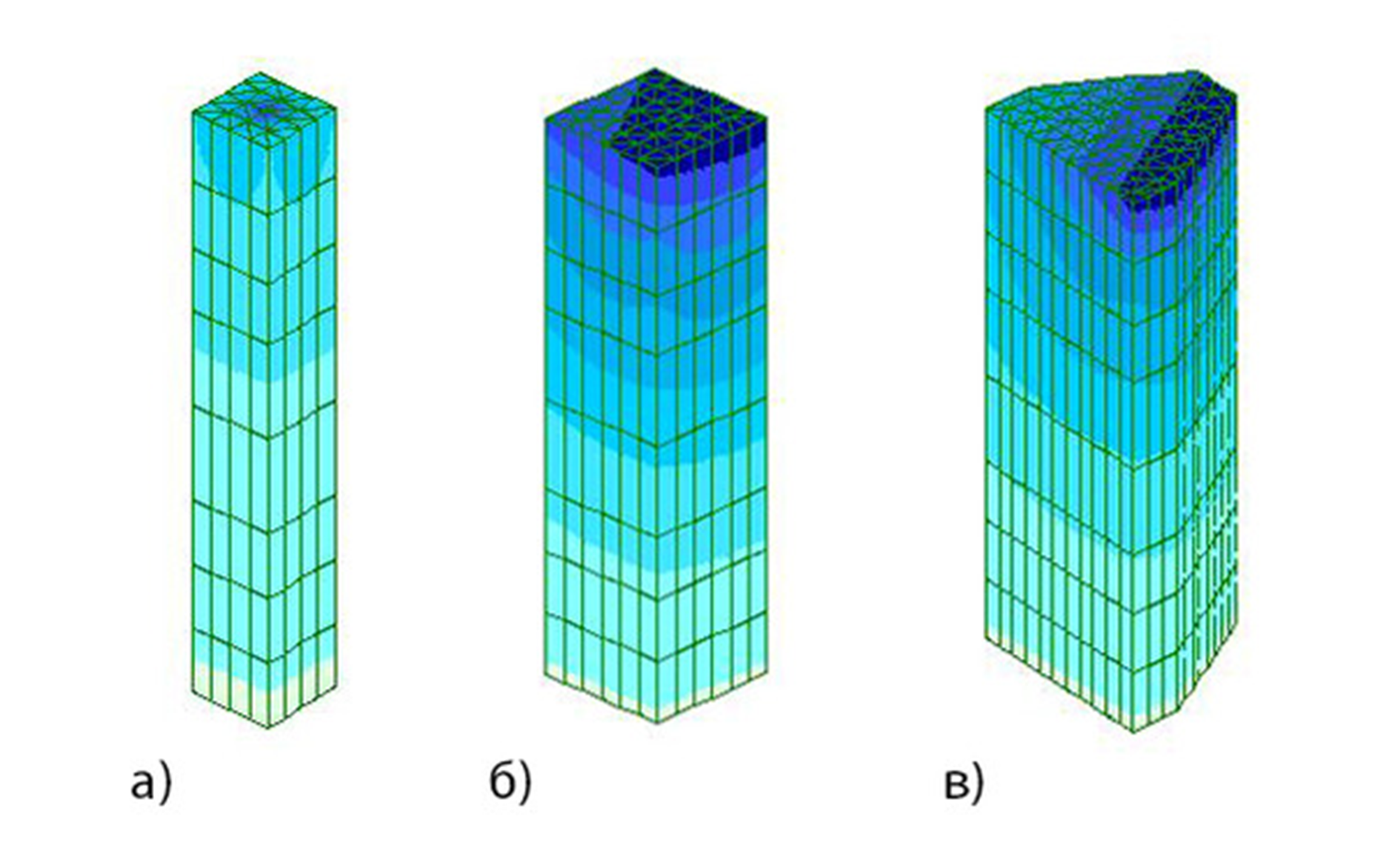
У другій задачі, ґрунтова основа була змодельована за допомогою об'ємних КЕ. Дана задача складається з двох частин: розрахунок основи в лінійній постановці, та з урахуванням фізичної нелінійності поведінки основи (при завданні різних критеріїв міцності). Комп'ютерну модель будівлі та ґрунтового масиву наведено на рисунку 2.

Якщо ґрунтове середовище моделювати як лінійно деформоване, у ПК «ЛІРА-САПР» реалізується обчислення осадки основи від заданих навантажень з використанням розрахункової схеми у вигляді лінійно деформованого напівпростору (задача Буссинеска). У цій моделі приймаються два припущення: перше – осадка  точки поверхні основи прямо пропорційна величині завантаження  у цій точці, друге – осадка розповсюджується і за межі площі завантаження.

На відміну від попереднього методу, модель лінійно деформованого напівпростору при спільному розрахунку споруди з основою дозволяє визначити крім контактних напружень, напружено-деформований стан ґрунту всієї основи.

При такому моделюванні основи, за допомогою об'ємних скінченних елементів, в якості вихідних даних вводяться тільки модуль загальних деформацій E, коефіцієнт Пуассона η та питома вага кожного шару. Товщина шару задається при завданні геометрії скінченних елементів. При цьому розрахункова модель фактично зводиться до стиснутого шару кінцевої міцності.

У розглянутій задачі, скінченним елементам були задані наступні характеристики шарів ґрунтового масиву:

ИГЭ-1 (E= 28000 кН/м2, n = 0,3), ИГЭ-2 (E= 25000 кН/м2, n = 0,3), ИГЭ-3 (E= 13000 кН/м2, n = 0,3), ИГЭ-4 (E= 16000 кН/м2, n = 0,35).

Але деформацію ґрунту можна описати за допомогою лінійної моделі середовища лише до певного рівня зусиль, за межами якого лінійний зв'язок напружень та деформацій порушується.

Необоротні деформації ґрунту, як гетерогенного середовища, виникають значно раніше за досягнення граничного стану, і вони суттєво перевищують пружні деформації. Тому розглянемо розрахунок осадки ґрунтового масиву з урахуванням фізично-нелінійної роботи основи.

При вирішенні цієї задачі, для моделювання роботи ґрунту, використовувався КЕ 273, який дозволяє враховувати односторонню роботу ґрунту з урахуванням зсуву. У даному випадку, у користувача є можливість обрати модель роботи ґрунту (по Кулону-Мору, Друккеру-Прагеру або Боткіну).

У прикладі, що розглядається, для чисельного моделювання нелінійних властивостей ґрунтового масиву, скінченним елементам №273 були задані наступні характеристики:

– ИГЭ-1 (E= 28000 кН/м2, n = 0,3, R0= 17,4 кН/м3, ke= 1, C= 2 кН/м2, Rt= 2 кН/м2, Fi= 32˚, Ϭp= 300 кН/м2);

– ИГЭ-2 (E= 25000 кН/м2, n = 0,3, R0= 19,3 кН/м3, ke= 1, C= 1 кН/м2, Rt= 1 кН/м2, Fi= 30˚, Ϭp= 300 кН/м2);

– ИГЭ-3 (E= 13000 кН/м2, n = 0,3, R0= 19,1 кН/м3, ke= 1, C= 12 кН/м2, Rt= 5 кН/м2, Fi= 23˚, Ϭp= 280 кН/м2);

– ИГЭ-4 (E= 16000 кН/м2, n = 0,35, R0= 19,1 кН/м3, ke= 1, C= 25 кН/м2, Rt= 30 кН/м2, Fi= 22˚, Ϭp= 250 кН/м2);

де C – зчеплення, R_t – граничне напруження при розтягуванні, яке було визначене із співвідношення F_i – кут внутрішнього тертя, Ϭ_p – граничне напруження стиснення.

Простою нелінійною моделлю роботи ґрунту є загальновідома ідеально пружно-пластична модель з граничною поверхнею, що визначається критерієм Кулона-Мора. Перевага моделі полягає у простоті призначення параметрів, які можна отримати зі звіту з інженерно-геологічних досліджень. Для цієї моделі умова міцності виражається по формулі:

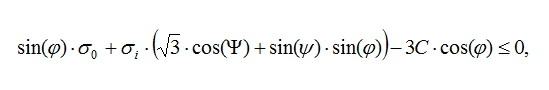
Однак, ця модель передбачає однакову поведінку матеріалу на стадії первинного завантаження та розвантаження, що зовсім не характерно для ґрунтів (у яких модуль завантаження та розвантаження відрізняється, як відомо, у 5...10 разів). Крім того, недоліком даної моделі є те, що в розрахунку виключено головне проміжне напруження та його вплив на ґрунт, що не відповідає дійсності, а наявність кутів на поверхні плинності ускладнює чисельне вирішення просторових задач. Ці недоліки виключені з розрахунку по критерію міцності Друккера-Прагера.

Модель Друккера-Прагера також реалізує пружну ідеально-пластичну поведінку ґрунтів. А поверхня пластичності згідно з моделлю Друккера-Прагера є правильним круговим конусом відносно гідростатичної осі  у просторовій системі головних напружень.

Умову міцності для моделі Друкера-Прагера виражають по формулі:

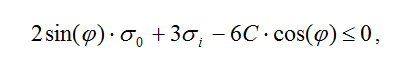
Також, у ПК «ЛІРА-САПР» реалізовано умову міцності ґрунту Боткіна. Відповідно до цієї умови, на відміну від Кулона-Мора, передбачається, що на міцність ґрунту впливають всі три головні напруження, а граничний стан настає на октаедричній площині (площина, є рівнопохилою до всіх головних напрямків напружень).

Умови міцності для моделі Боткіна:

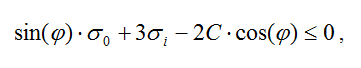
Порівняння та аналіз результатів розрахунку було виконано по ряду показників: напружений стан найбільш завантажених колон, величина максимального прогину консольних стержневих елементів конструкції, кінематичні характеристики – переміщення розрахункових характерних точок будівлі за напрямком «Z».

Чисельні значення максимальних прогинів консолей для кожного варіанту моделювання ґрунтової основи наведені в таблиці 1. Номери секцій будівлі показані на рисунку 3.

Таблиця 1. Максимальні прогини консольних частин будівлі, мм

З таблиці видно, що отримані переміщення по результатах розрахунку при нелінійній постановці значно вищі, ніж при використанні коефіцієнтів постелі та CЕ 34. Це пояснюється тим, що CЕ 273 краще моделює поведінку основи, робота якого, безсумнівно, впливає на НДС елементів конструкції.

На рисунку 4 показано порівняння значень поздовжніх зусиль, що виникають у скінченних елементах, які моделюють роботу найзавантаженіших колон секції 2.

Результати розрахунку в лінійній постановці задачі та з урахуванням фізичної нелінійності основи характеризуються значним ступенем подібності. А похибка в результатах по різних варіантах моделювання нелінійної роботи основи менша 1%. Це вказує на те, що вибір методу опису нелінійної деформації елементів майже не відіграє ролі при визначенні несучої здатності та підборі перерізів елементів конструкції.

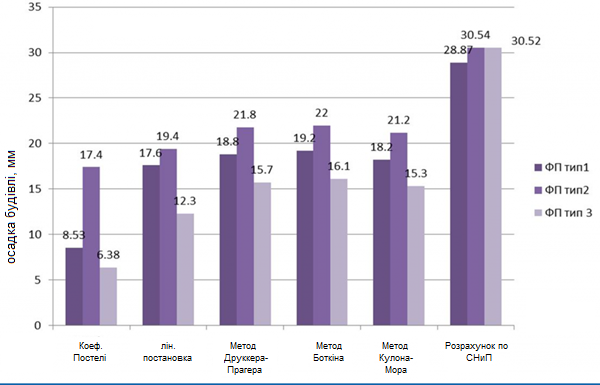
На рисунку 6 наведена гістограма по вертикальних переміщеннях розрахункових характерних точок фундаментних плит (ФП), які позначені колами на рисунку 5. Ізополя вертикальних переміщень, які розглянуті ФП, показані на рисунку 7.

ВИСНОВКИ

Виконаний аналіз НДС по різних варіантах моделювання ґрунтового масиву показав, що максимальні значення осадки були отримані при розрахунку методом пошарового підсумовування. Різниця між чисельним моделюванням основи та при розрахунку ґрунтового масиву по методиці лінійно-деформованого напівпростору з умовним обмеженням глибини товщини, що стискається, можна аргументувати декількома факторами:

• у кожному елементарному шарі вертикальні напруження приймаються як середнє значення між додатковим тиском на вершині та на підошві кожного шару. Така апроксимація епюр напружень не дає достатньої можливості описати роботу дисперсного середовища;
• відсутність сил взаємодії між елементарними шарами;
• у методі пошарового підсумовування не враховується нелінійна зміна величини модуля деформацій для кожного елементарного шару.

Похибка при розрахунках осадки будівлі по різних методах моделювання нелінійної роботи ґрунту становить переважно менше 1%. При врахуванні пластичної роботи основи метод Кулона-Мора показав найменші значення осадки. Це можна пояснити тим, що дана модель не враховує впливу головного проміжного напруження. Цей фактор був врахований у методі Боткіна, де береться до уваги зв'язок інтенсивності дотичних напружень та середнього тиску. Саме при використанні цього методу було отримано максимальне значення осадки конструкції при комп'ютерному моделюванні системи.

• чисельне моделювання
• напружено-деформований стан
• осадка
• метод пошарового сумування
• фізична нелінійність