Цель:
Определение напряженно-деформированного состояния тора под внутренним давлением.
Литература:
R.J. Roark et W.C. Young, Formulas for stress and strain, 5e edition, New York, McGraw-Hill, 1975.
Формулировка задачи:
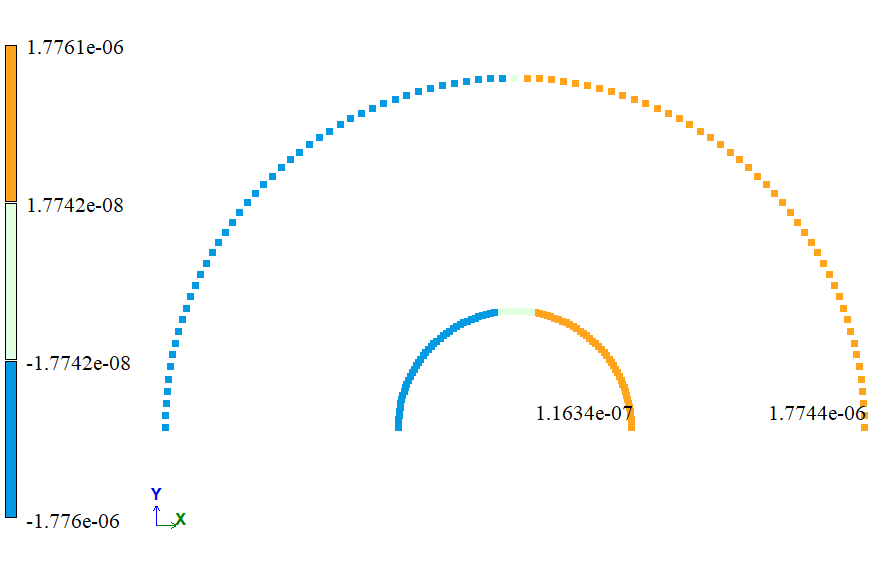
Определить радиальные перемещения ΔR на внутренних и внешних направляющих тора, а также напряжения σ11 и σ22 в его стенках.
Описание расчетной схемы:
Тор свободен от закреплений под воздействием внутреннего равномерного давления q.
|
а |
б |
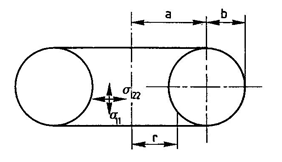
Геометрия:
Радиус образующей b = 1 м;
Расстояние от центра вращения до центра образующей a = 2 м;
Толщина стенки h = 0,02 м.
Характеристика материала:
Модуль упругости Е = 2,1 * 1011 Па;
Коэффициент Пуассона ν = 0,3.
Граничные условия:
Связи симметрии.
Нагрузки:
Равномерно распределенная по площади P = 10000 Па.
Примечание:
Задача решается в пространственной постановке (признак схемы 5).
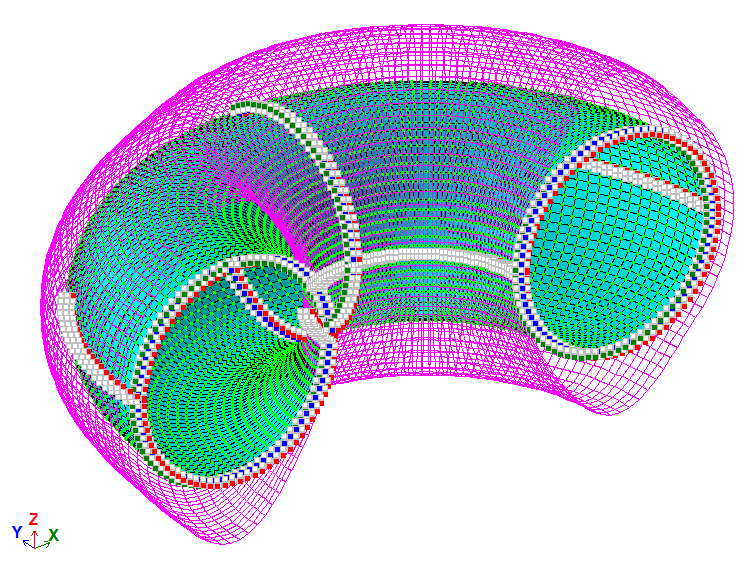
Для построения схемы использованы КЭ 44 – универсальный четырехугольный КЭ оболочки.
В расчетной схеме рассмотрен фрагмент тора (180°). Для учета отсеченной части приложены связи симметрии.
Сетка конечных элементов имеет 80 элементов вдоль окружности круга сечения и 90 элементов вдоль окружности стенки.
Количество узлов: 7280. Количество элементов: 7200.
Результаты расчета:
|
а |
б |
Аналитическое решение:
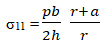

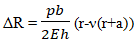
Сравнение результатов расчета:
Без дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| ∀r | σ22, Па | 2,5 * 105 | 2,4915 * 105 | 0,34 |
| r = a - b | σ11, Па | 7,5 * 105 | 7,4917 * 105 | 0,1107 |
| ΔR, м | 1,19 * 10-7 | 1,1634 * 10-7 | 2,2353 | |
| r = a + b | σ11, Па | 4,17 * 105 | 4,1663 * 105 | 0,0887 |
| ΔR, м | 1,79 * 10-6 | 1,7744 * 10-6 | 0,8715 |
С использованием дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| ∀r | σ22, Па | 2,5 * 105 | 2,4941 * 105 | 0,236 |
| r = a - b | σ11, Па | 7,5 * 105 | 7,4739 * 105 | 0,348 |
| ΔR, м | 1,19 * 10-7 | 1,2349 * 10-7 | 3,6359 | |
| r = a + b | σ11, Па | 4,17 * 105 | 4,1668 * 105 | 0,0676 |
| ΔR, м | 1,79 * 10-6 | 1,7732 * 10-6 | 0,9385 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.



Комментарии