Цель:
Определение напряженно деформированного состояния консольной пластины.
Литература:
S. Timoshenko, Résistance des matériaux, t. 1, Paris, Librairie Polytechnique Ch. Béranger, 1949.
Формулировка задачи:
Определить вертикальное перемещение Z(w) свободного края пластины, а также изгибающий момент в жестком закреплении.
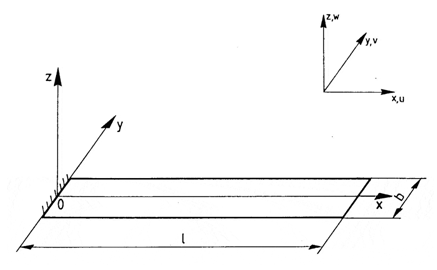
Описание расчетной схемы:
Консольная пластина, загруженная равномерно распределенной нагрузкой q.
|
а |
б |
Геометрия:
Толщина пластины h = 0,005 м;
Вылет консоли l = 1 м;
Относительная толщина пластины h/l = 0,005;
Ширина пластины b = 0,1 м.
Характеристика материала:
Модуль упругости Е = 2,1 * 1011 Па;
Коэффициент Пуассона ν = 0.
Граничные условия:
Связи на левой грани пластины жестко ущемлены по всем степеням свободы КЭ плиты (Z, uX, uY).
Нагрузки:
Равномерно распределенная нагрузка по площади: q = 1700 Па.
Примечание:
Задача решается в плоской постановке (признак схемы 3 – плоскость XOY).
Для построения схемы использованы КЭ 11 – прямоугольная КЭ плиты. КЭ 11 имеет три степени свободы в узле – перемещение вдоль глобальной оси Z и повороты вокруг глобальных осей uX и uY.
Размер конечных элементов: 0,01 × 0,01 м.
Количество узлов: 1111. Количество элементов: 1000.
Результаты расчета:
|
Изополя вертикальных перемещений Z(w), м
|
Мозаика изгибающих моментов Мх, Н*м/м
|
Аналитическое решение:
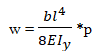
M = −ql2/2
Сравнение результатов расчета:
Без дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| x = 1 | Вертикальное перемещение, м | -0,0973 | -0,0972 | 0,1028 |
| x = 0 | Изгибающий момент, Н*м/м | -850 | -842,38 | 0,8965 |
С использованием дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| x = 1 | Вертикальное перемещение, м | -0,0973 | -0,0972 | 0,1028 |
| x = 0 | Изгибающий момент, Н*м/м | -850 | -842,36 | 0,8988 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.




Комментарии