Цель:
Определение напряженно-деформированного состояния балки с затяжкой с учетом деформаций поперечного сдвига в балке.
Литература:
M. Laredo, Résistance des matériaux, Paris, Dunod, 1970, P. 77.
Формулировка задачи:
Определить продольное усилие в затяжке РЕ, изгибающий момент М в балке в точке Н и вертикальное перемещение v(Z) в точке D.
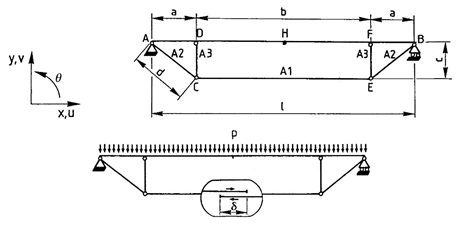
Описание расчетной схемы:
Однопролетная балка с затяжкой, стянутой на величину смещения δ, загружена равномерно распределенной нагрузкой q.
Геометрия:
Длина стержней а = 2 м; b = 4 м; l = 8 м; с = 0,6 м; d = 2,088 м;
Площадь поперечного сечения балки AD, DF, FB: А = 0,01516 м2; Аr = A/2,5 = 0,006064 м2;
Момент инерции балки I = 2,174 * 10-4 м4;
Площадь поперечного сечения стержней AC, CE, EB: А1 = А2 = 4.5 * 10-3 м2;
Площадь поперечного сечения стержней DC, FE: А3 = 3,48 * 10-3 м2.
Характеристика материала:
Модуль упругости Е = 2,1 * 1011 Па;
Модуль сдвига G = 0,4 * Е = 0,84 * 1011 Па.
Граничные условия:
В точках А и В заданы связи, которые запрещают перемещение по вертикали вдоль глобальной оси Z (Z (vA, vВ) = 0). В точке Н перенесена связь, запрещающая перемещение по горизонтали вдоль глобальной оси Х (X(uH) = 0), для симметрии перемещений.
Нагрузки:
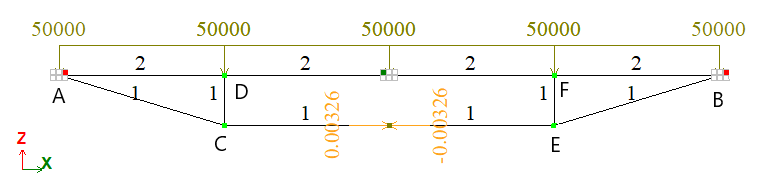
Интенсивность равномерно распределенной нагрузки q = 50000 Н/м.
Величина зміщення δ = 6,52 * 10-3 м.
Примечание:
Задача решается в плоской постановке (признак схемы 2 – плоскость XOZ).
Для описания работы затяжки (стержни AC, CE, EB) и распорок (стержни DC, FE) использованы КЭ 1 – КЭ плоской фермы. Для описания работы балки (стержни AD, DF, FB) использованы КЭ 2 – КЭ плоской рамы (с учетом сдвига). Поскольку узлы КЭ 1 имеют две степени свободы – перемещение вдоль глобальных осей X и Z, то соединение этих элементов в узлах является шарнирным.
Для задания нагрузки от вынужденного смещения стержень КЭ был разделен на 2 элемента с расшивкой узлов. Нагрузка прикладывалась к каждому из расшитых узлов.
При этом величина вынужденного смещения каждого узла δi = δ/2 = 3,26 * 10-3 м.
Количество узлов: 9. Количество элементов: 12.
Результаты расчета:
|
Расчетная и деформированная схема балки |
Мозаика вертикальных перемещений v(Z), м |
|
Мозаика продольных усилий N, Н |
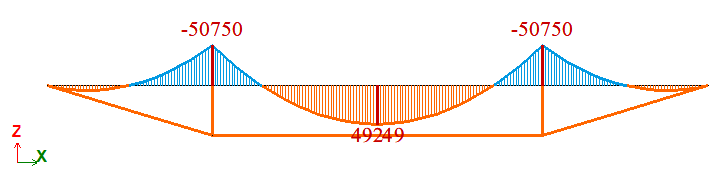
Эпюра изгибающих моментов М, Н*м |
Аналитическое решение:
μ = 1-(4/3)(a/l)
k = A/Ar = 2,5
t = √(I/A)
γ = (l/c)2(1+(A/A1)(b/l)+2(A/A2)(d/a)2(d/l)+2(A/A3)(C/A)2(c/a)2(c/l))
τ = k(2Et2/(Gal))
ρ = μ+γ+τ
μ0 = 1-(a/l)2(2-a/l)
τ0 = 6k(E/G)(t/l)2(1+b/l)
ρ0 = μ0+ τ0
NCE = -(1/12)(pl2/c)(ρ0/ρ)+(EI/(lc2))(δ/ρ)
MH = -(1/8)pl2(1-(2/3)(ρ0/ρ))-(EI/(lc))(δ/ρ)
Сравнение результатов расчета:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| КЭ | Продольное усилие, Н | 584584 | 58458 | 0,0007 |
| Н | Момент М, Н*м | 49249,5 | 49249,5 | 0 |
| D | Перемещение vD, м | -0,0005428 | -0,0005428 | 0 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.



Комментарии