Цель:
Определение напряженно деформированного состояния пространственной стержневой системы с упругими связями под действием сосредоточенной силы.
Литература:
M. Laredo, Résistance des matériaux, Paris, Dunod, 1970, P. 165.
Формулировка задачи:
Определить вертикальное перемещение Z для узла соединения стержней AD и HD (точка D), горизонтальное перемещение и угол поворота точки А, а также крутящий и изгибающий моменты Mx, My, Mz для узлов закрепления пространственной системы (точки А, В).
Описание расчетной схемы:
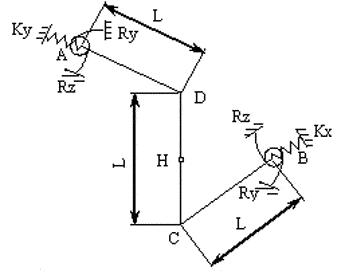
Пространственная система состоит из четырех стержней. Горизонтальные стержни ортогонально лежат в параллельных горизонтальных плоскостях и соединены вертикальными стержнями, которые соединяются шарнирно между собой (точка Н).
В опорных узлах пространственной системы (точки А, В) установлены жесткие связи по направлениям линейных и угловых степеней свободы в плоскости поперечного сечения и упругие связи по направлениям линейной и угловой степеней свободы из плоскости поперечного сечения.
В узле соединения верхнего горизонтального и вертикального стержней (точка D) приложена вертикальная сосредоточенная сила F.
| Начальная геометрия аналитической схемы | |
|
а |
б |
Геометрия:
Длина горизонтальных стержней L = 2 м;
Длина вертикальных стержней 0,5L = 1 м;
Моменты инерции сечения Iy = Ix = I = 10-6 м4;
Полярный момент инерции (постоянная кручения) J = 2 * 10-6 м4;
Площадь сечения A = 0,001 м2.
Характеристика материала:
Модуль упругости Е = 2,1 * 1011 Па;
Модуль сдвига G = 7,875 * 1010 Па.
Граничные условия:
В точке А: жесткие связи по направлениям степеней свободы uY (θY=0), X і Z (uA=wA=0);
связи конечной жесткости по направлениям степеней свободы Y, uX, uZ: Rу = 52500 Н/м, Rux = Ruz = 52500 Н*м/рад.
В точке В: жесткие связи по направлениям степеней свободы uX (θX=0), Y і Z (uB=wB=0);
связи конечной жесткости по направлениям степеней свободы X, uY, uZ: Rх = 52500 Н/м, Ruy = Ruz = 52500 Н*м/рад.
В точке Н: шарнир.
Нагрузки:
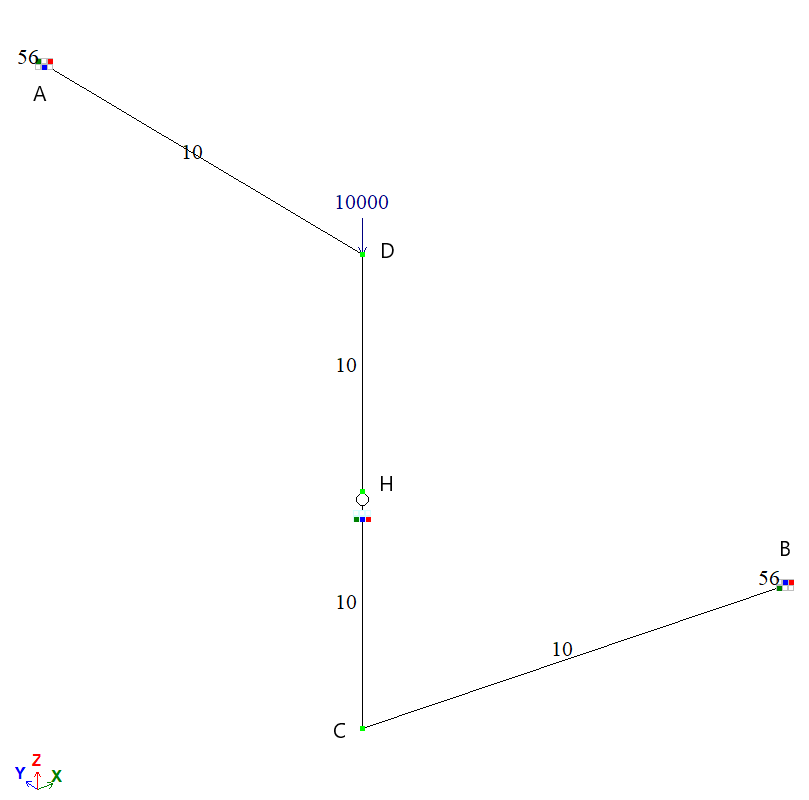
Вертикальная сосредоточенная сила F = 10000 Н, приложенная в точке D.
Примечание:
Задача решается в пространственной постановке (признак схемы 5).
Для построения схемы использованы КЭ 10 – универсальный пространственный стержневой КЭ.
Связи конечной жесткости в точках А и В заданы с помощью КЭ 56 – одноузловой КЭ упругих связей.
В точке Н стержня CD введен шарнир по направлениям степеней свободы uY, uX, uZ.
Количество узлов: 5. Количество элементов: 6.
Результаты расчета:
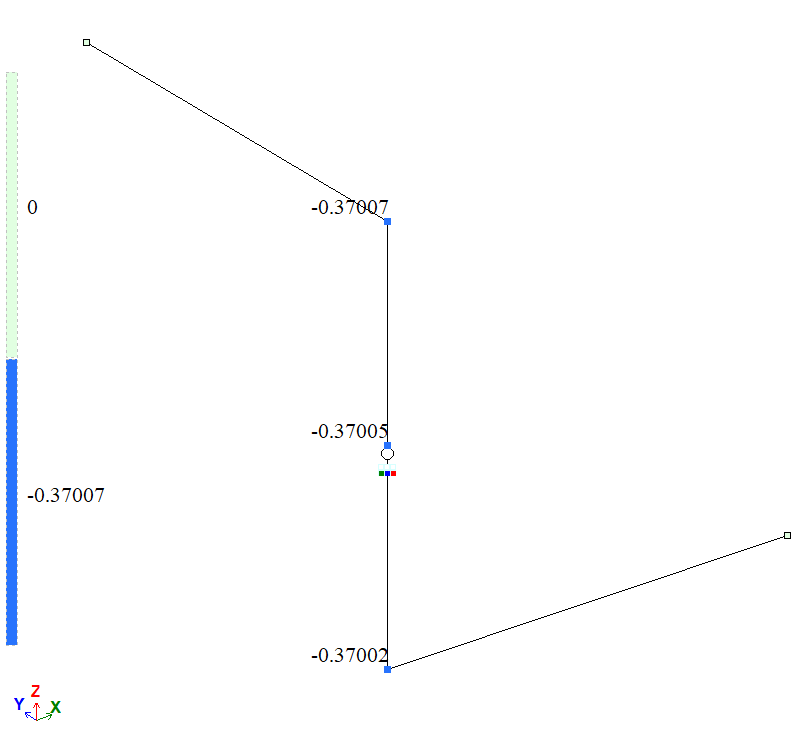
|
Мозаика вертикальных перемещений вдоль глобальной оси Z (w), м |
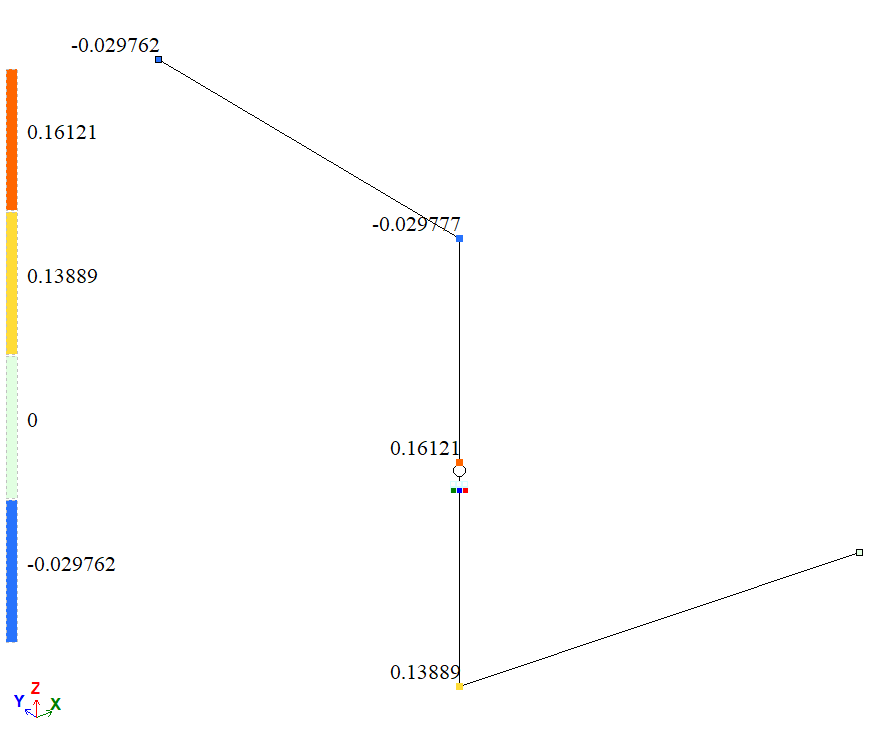
Мозаика горизонтальных перемещений вдоль глобальной оси Y (v), м |
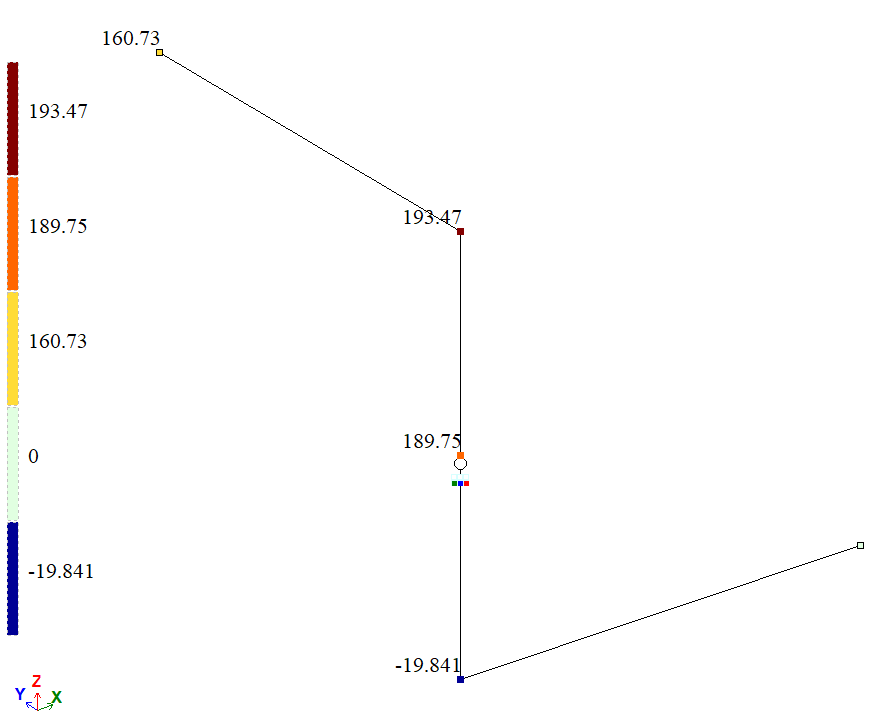
Мозаика углов поворота вокруг глобальной оси Х (u), рад*1000 |
|
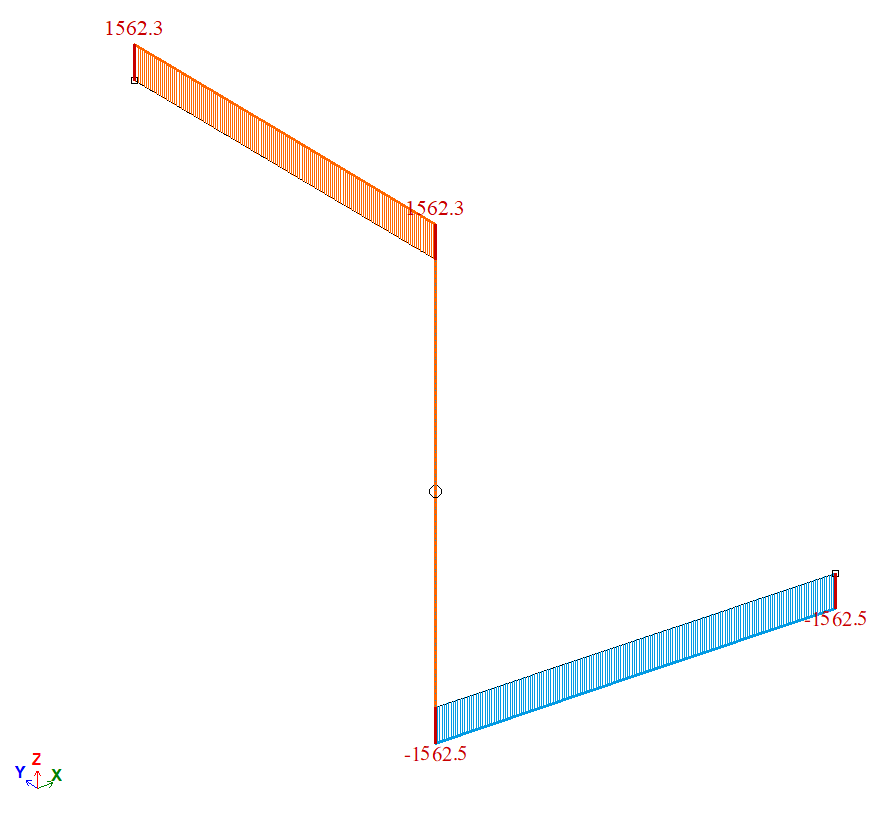
Эпюра крутящих моментов Мх, Н*м
|
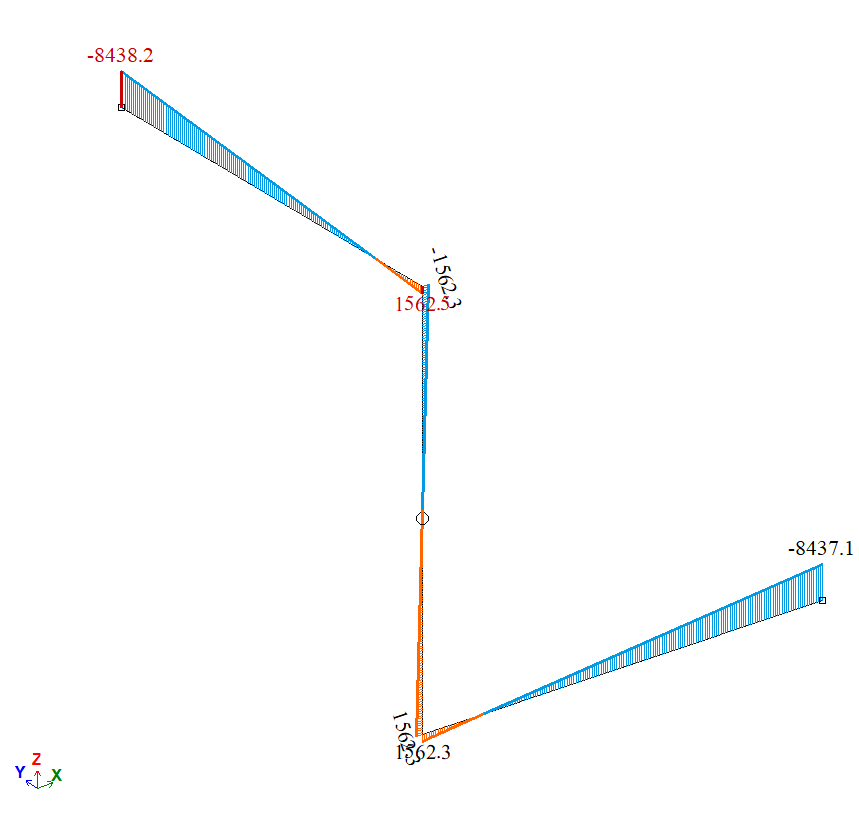
Эпюра изгибающих моментов Му, Н*м
|
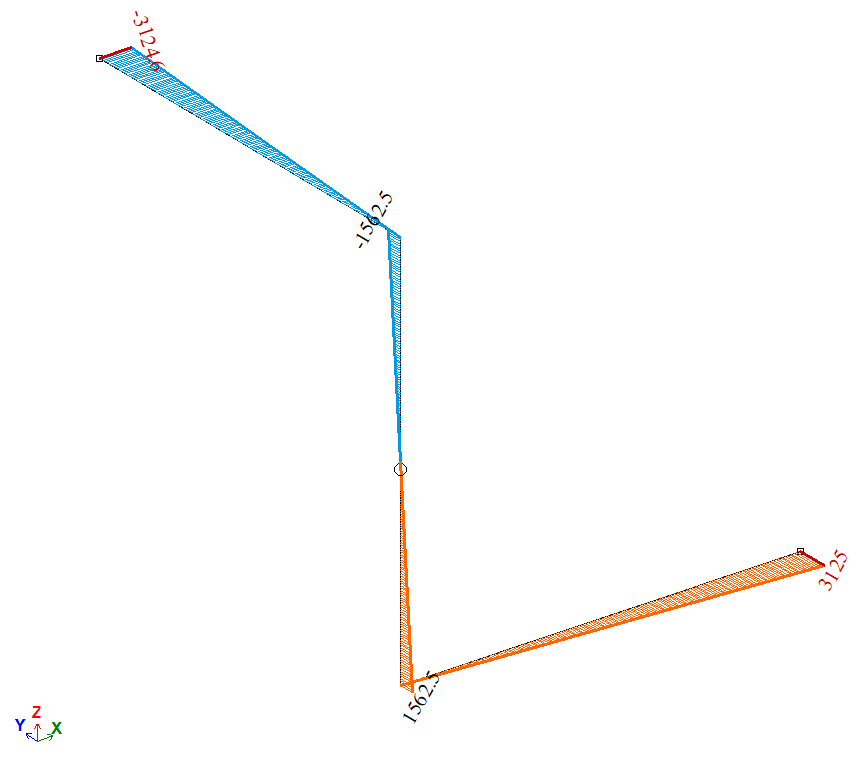
Эпюра изгибающих моментов Мz, Н*м
|
Аналитическое решение:
MAx = 5*F*l/64
MAy = 27*F*l/64
MAz = -5*F*l/32
MBx = -27*F*l/64
MBy = -5*F*l/64
MBz = -5*F*l/32
νA = 5*F*l/(64*EI)
θAx = -27*F*l2/(32*EI)
ωD = 373*F*l3/(384*EI)
Сравнение результатов расчета:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| А | Момент Мх, Н*м | 1562,5 | 1562,3 | 0,0128 |
| А | Момент Му, Н*м | 8437,5 | 8438,2 | 0,083 |
| А | Момент Мz, Н*м | 3125 | 3124,6 | 0,0128 |
| B | Момент Мх, Н*м | 1562,5 | 1562,5 | 0 |
| B | Момент Му, Н*м | 8437,5 | 8437,1 | 0,0047 |
| B | Момент Мz, Н*м | 3125 | 3125 | 0 |
| А | Перемещение νA, м | 0,02976 | 0,02977 | 0,001 |
| А | Угол поворота θAX, рад | 0,16071 | 0,16073 | 0 |
| D | Перемещение ωD, м | 0,37004 | 0,37007 | 0,0027 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Комментарии