Цель:
Определение напряженно деформированного состояния плоской фермы при силовом, температурном и кинематическом воздействиях.
Литература:
M. Laredo, Résistance des matériaux, Paris, Dunod, 1970, P. 579.
Формулировка задачи:
Определить продольное усилие в опорном подкосе BD и вертикальное перемещение v в точке D.
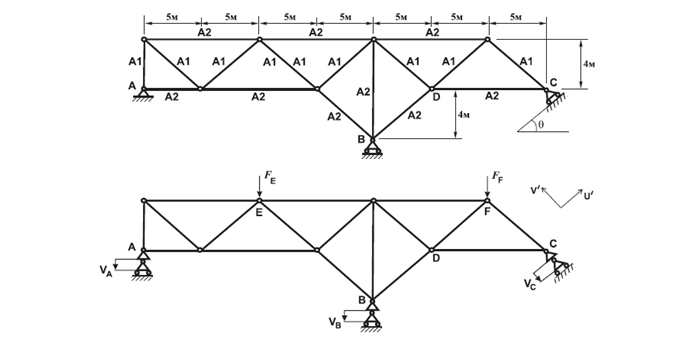
Описание расчетной схемы:
Двухпролетная ферма нагружена двумя сосредоточенными силами FE и FF в узлах верхнего пояса, равномерно нагретая во всех поперечных сечениях элементов на величину ΔT и подвергается воздействию смещения её опор на величины VA, VB и VC.
Геометрия:
Угол наклона опорной площадки в узле С к горизонту θ = 30°;
Площадь сечения стержней А1 = 1,41 * 10-3 м2; А2 = 2,82 * 10-3 м2.
Характеристика материала:
Модуль упругости Е = 2,1 * 1011 Па;
Коэффициент температурного расширения α = 10-5 С-1.
Граничные условия:
В линейных и нелинейных задачах связь в направлении заданного смещения не накладывается.
Поскольку все нагрузки приложены в одном загружении, то схема закреплена только в узле А от смещения вдоль глобальной оси Х (Х(uA) = 0).
Нагрузки:
Вынужденные смещения: VA = -0,02 м; VВ = -0,03 м; VC = -0,015 м;
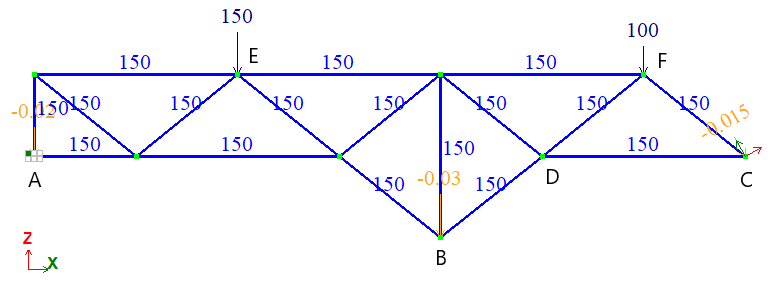
Вертикальные сосредоточенные силы: FE = 150 кН; FF = 100 кН;
Все стержни нагреты до температуры 150 °С.
Примечание:
Задача решается в плоской постановке (признак схемы 1 – плоскость XOZ).
Для построения схемы использованы КЭ 1 – КЭ плоской фермы. Поскольку узлы КЭ 1 имеют две степени свободы – перемещение вдоль глобальных осей X и Z, то соединение этих элементов в узлах является шарнирным.
Для узла в точке С предназначена местная система координат, в которой ось Х1 совпадает с направлением заданной в этом узле нагрузки.
Количество узлов: 10. Количество элементов: 17.
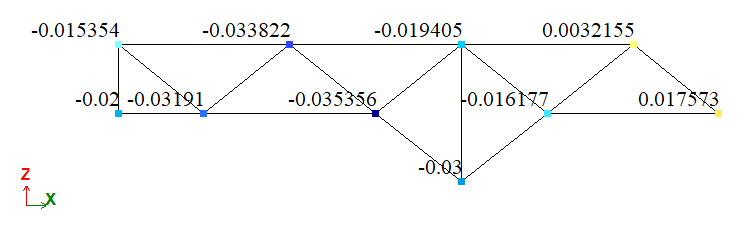
Результаты расчета:
Сравнение результатов расчета:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| D | Перемещение VD, м | -0,01618 | -0,016177 | 0,0185 |
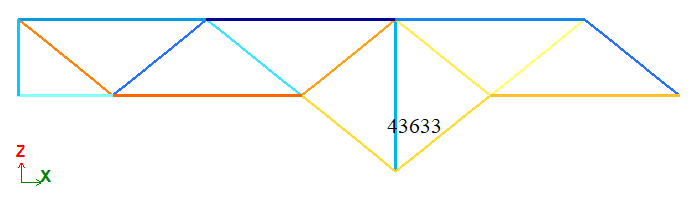
| BD | Продольное усилие, Н | 43633 | 43633 | 0 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Комментарии