Цель:
Определение напряженно деформированного состояния призматического бруса под действием изгибающего момента.
Литература:
S. Timoshenko, Théorie de l’élasticité, Paris, Librairie Polytechnique Ch. Béranger, 1961, P. 284-289.
Формулировка задачи:
Определить перемещение по Х в точке А, Z в точке B и по Y в точке D, E, F, G.
Описание расчетной схемы:
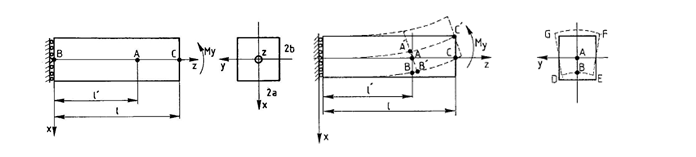
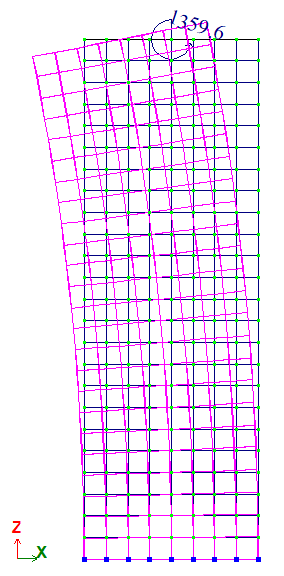
Консольный призматический брус, загруженный изгибающим моментом возле свободного края.
|
Вариант 1 |
Вариант 2 |
Геометрия:
Длина l = 6 м;
Размеры сечения a = b = 1 м;
Ордината контрольного сечения l′ = (2/3)l = 4 м.
Характеристика материала:
Модуль упругости Е = 2 * 105 МПа;
Коэффициент Пуассона ν = 0,3.
Граничные условия:
Связи по всем перемещениям в точке B (X=Y=Z=0).
На плоскости, проходящей через точку В – связи, запрещающие перемещение по Z, и связи симметрии.
Нагрузки:
В точке С приложен момент вокруг оси Y, My = 4/3 * 107 Н*м = 1359,62 т*м.
Примечание:
Задача решается в пространственной постановке (признак схемы 5).
Для построения схемы использованы КЭ 31 – параллелепипед.
В расчетной схеме рассматривается вся призма.
Для приложения моментной нагрузки на торец призмы был задан «паук» из стержневых КЭ 10 (моделирование АЖТ на изгиб из плоскости торца призмы и с нулевой жесткостью в плоскости, чтобы не ограничивать поперечные деформациий, т.е. задана большая изгибная жесткость из плоскости сечения и нулевая осевая и изгибная жесткости в плоскости сечения).
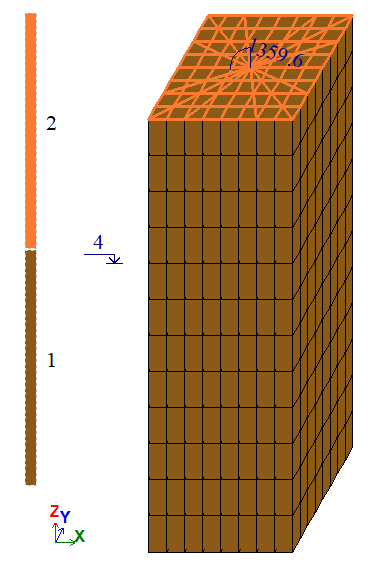
Вариант 1:
Сетка 8×8×12.
Количество узлов: 1053. Количество элементов: 944.
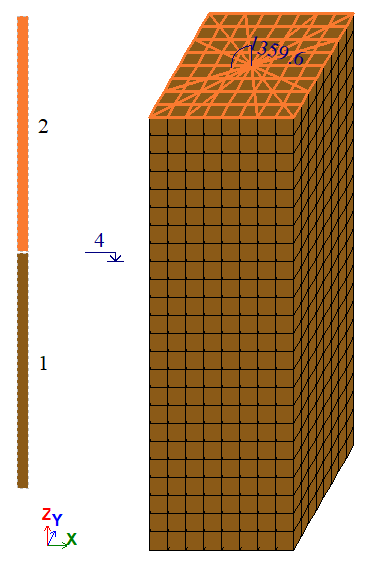
Вариант 2:
Сетка 8×8×24.
Количество узлов: 2025. Количество элементов: 1712.
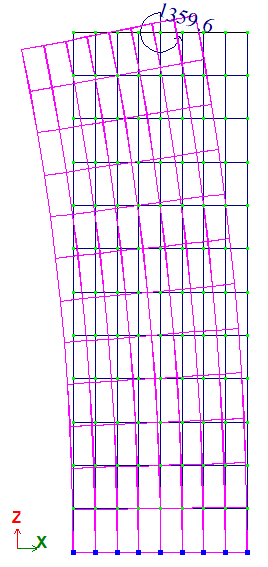
Результаты расчета:
|
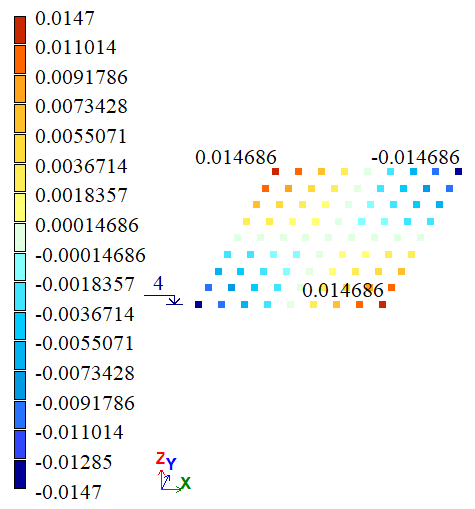
Вариант 1 |
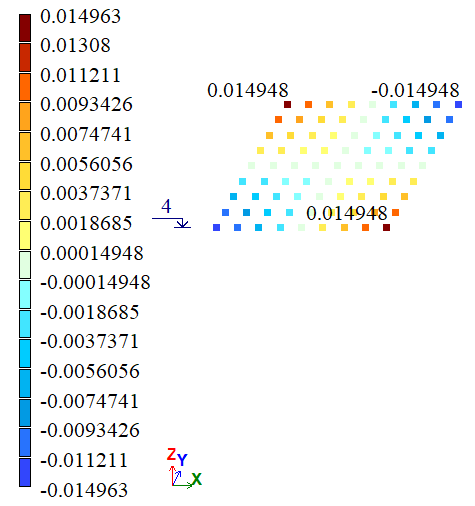
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
Аналитическое решение:
σxx = σyy = σxy = σyx = σzx = 0
u = -l’2/2R
w = l’2/R
v = ν(a2/R)
Сравнение результатов расчета:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % | ||
| Вариант 1 | Вариант 2 | Вариант 1 | Вариант 2 | |||
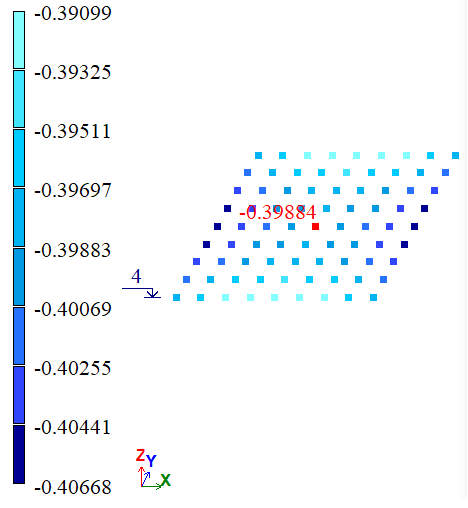
| А | Х, м | -4*10-4 | -3,9174*10-4 | -3,9884*10-4 | 2,065 | 0,29 |
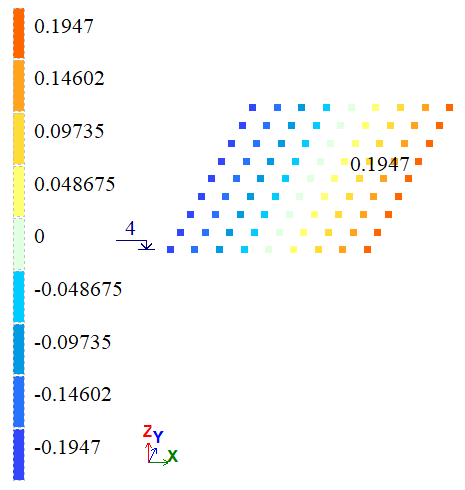
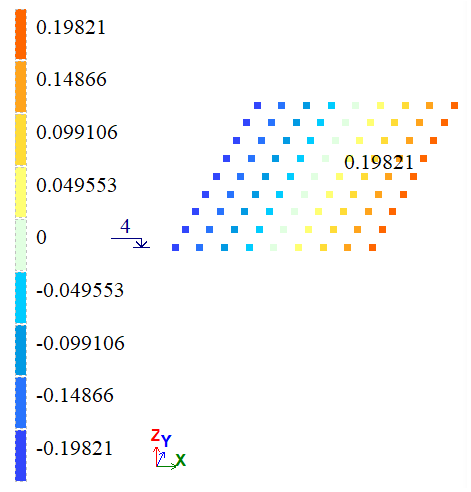
| А | Х, м | 2*10-4 | 1,947*10-4 | 1,9821*10-4 | 2,65 | 0,895 |
| F, G, D, E | Y, м | 0,15*10-4 | 0,14686*10-4 | 0,14948*10-4 | 2,0933 | 0,3467 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Комментарии