Цель:
Определение напряженно-деформированного состояния балки на упругом основании под действием сосредоточенных сил и распределенной нагрузки, изменяющейся по закону треугольника.
Формулировка задачи:
Определить вертикальные перемещения Z концов балки, а также изгибающие моменты Мy, поперечные силы Qz и углы поворота uY по ее длине.
Описание расчетной схемы:
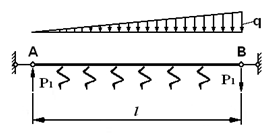
Балка на упругом основании, загруженная взаимоуравновешенными сосредоточенными силами на концах и распределенной по длине нагрузкой, изменяющейся по закону треугольника.
Геометрия:
Длина l = 10 м;
Момент инерции I = 2 * 10-6 м4;
Площадь поперечного сечения A = 0,003 м2;
Сдвижная площадь F = 0,0025 м2.
Характеристика материала:
Модуль упругости Е = 2,1 * 107 тс/м2;
Модуль сдвига G = 7,875 * 106 тс/м2.
Граничные условия:
Характеристики упругого основания: С1 = 500 тс/м3; С2 = 100 тс/м. Связи на концах балки по степеням свободы, запрещающие перемещение в направлении ее оси X (uA = uВ = 0).
Нагрузки:
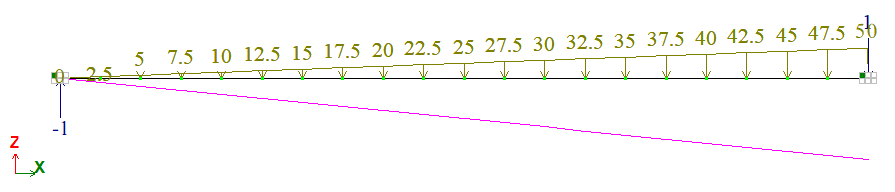
Неравномерно распределенная нагрузка: q = 50 тс/м;
Вертикальная сосредоточенная сила: Р1 = −Р1 = 1 тс.
Примечание:
Задача решается в плоской постановке (признак схемы 2 – перемещения X,Z,Uy).
Для построения схемы использованы КЭ 10 – универсальный пространственный стержневой КЭ.
Упругое основание характеризуется двумя коэффициентами постели (модель Пастернака), приложенными для ширины лунки осадки. Вс = 100 см.
Количество узлов: 21. Количество элементов: 20.
Результаты расчета:
Аналитическое решение:
w = −qx / (C1q)
M = 0
Q = −C2q / C1
Сравнение результатов расчета:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % |
| А | Перемещение wA, м | 0 | 0 | 0 |
| В | Перемещение wB, м | -0,1 | -0,1 | 0 |
| Любая | Угол поворота θY, рад | 0,01 | 0,01 | 0 |
| Сила Qz, тс | 1 | 1 | 0 | |
| Момент Мy, тс*м | 0 | 0 | 0 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

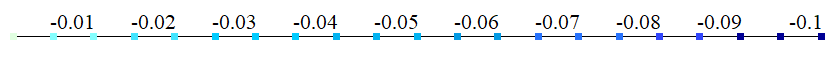
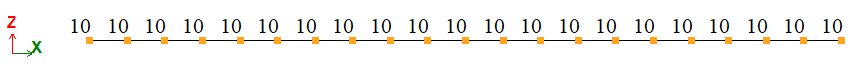

Комментарии