Цель:
Деформированное состояние трехступенчатой шарнирно-опертой балки, нагруженной сосредоточенными силами, без учета деформации поперечного сдвига. Проверяются поперечные перемещения и углы поворота.
Литература:
Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. - Киев: Наук. думка, 1988.
Формулировка задачи:
Определить углы поворота сечений и поперечные перемещения в местах приложения сил.
Описание расчетной схемы:
Трехпролетная шарнирно-подпертая балка нагружается тремя сосредоточенными силами P.
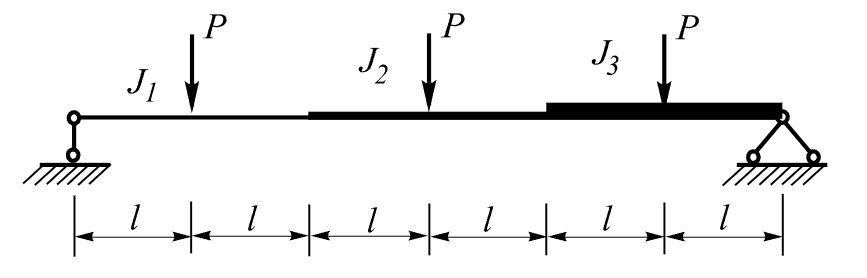
Начальная геометрия аналитической схемы
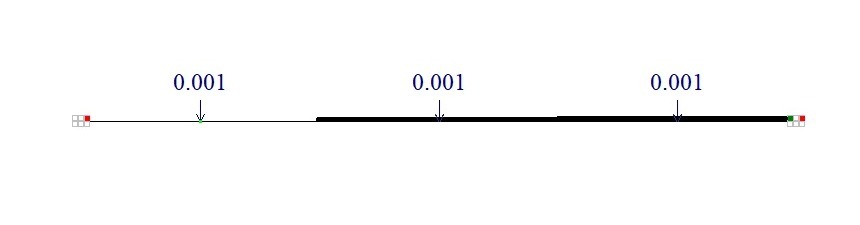
Начальная геометрия КЭ модели
Геометрия:
Длина полупролета балки каждого сечения L = 1 м;
Момент инерции I = 5 * 10-6 м4;
Площадь поперечного сечения F = 1 * 10-2 м2;
I1 : I2 : I3 = 1 : 2 : 3;
F1 : F2 : F3 = 1 : 2 : 3
Характеристика материала:
Модуль упругости Е = 2,0 * 1011 Па
Нагрузки:
Значение давления q = 10 кН/м.;
Значение нагрузки P = 1 кН.
Примечание:
Расчетная схема — общая система 6 стержневых элементов типа 2, 7 узлов.
Результаты расчета:
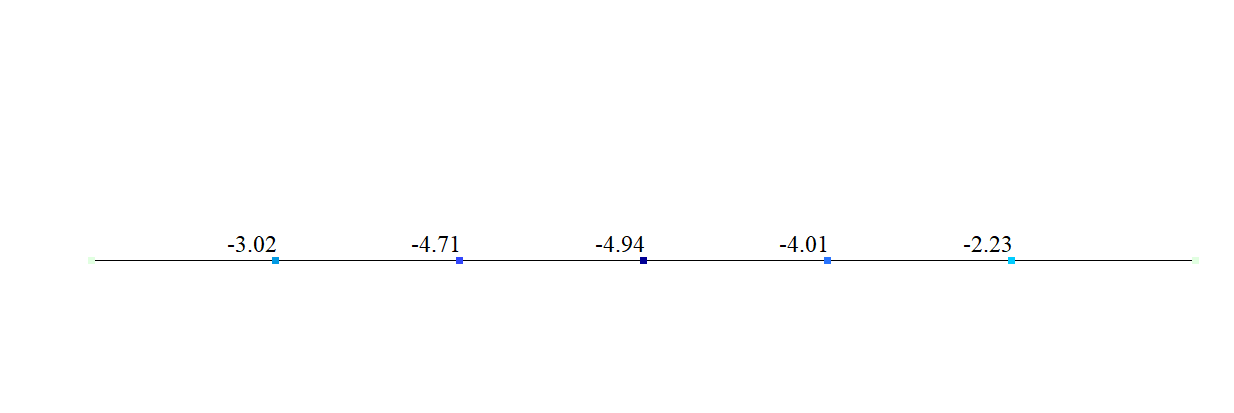
Значение поперечных перемещений w (мм)
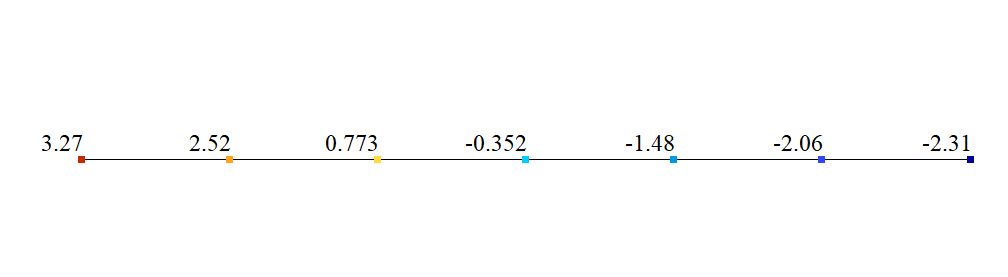
Значение углов поворота θ (рад*1000)
Аналитическое решение:
При аналитическом решении углы поворота опорных сечений и прогибы в местах приложения сосредоточенных сил определяются по формулам:
Сравнение результатов расчета:
| Параметр |
Аналитическое решение |
LIRA-FEM |
Погрешность, % |
| Поперечные перемещения, мм |
| w (l) |
-3.02 |
-3.02 |
0 |
| w (3l) |
-4.94 |
-4.94 |
0 |
| w (5l) |
-2.23 |
-2.23 |
0 |
| Углы поворота θ (рад*1000) |
| θ (0) |
3.27 |
3.27 |
0 |
| θ (6l) |
-2.31 |
-2.31 |
0 |
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.


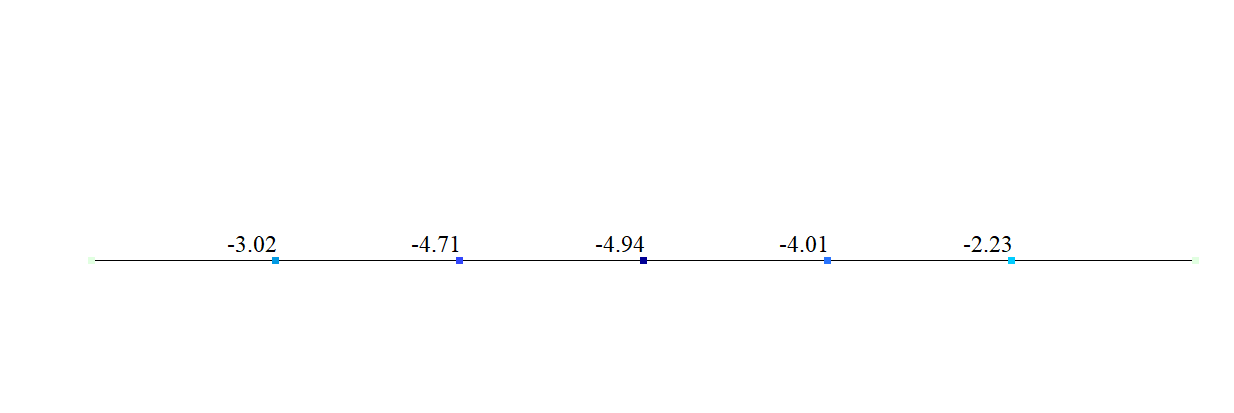
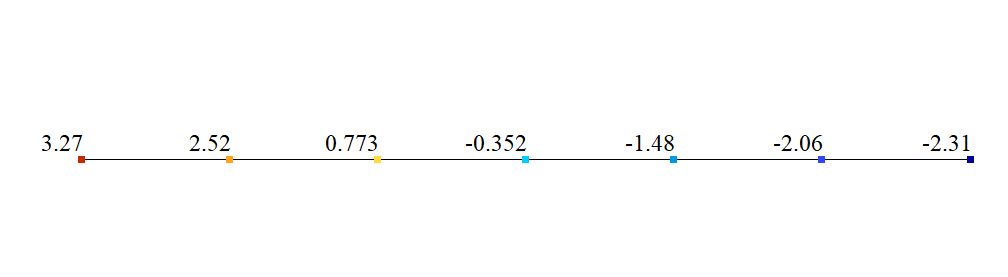
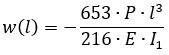
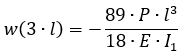
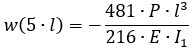
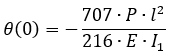
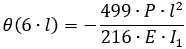
Комментарии