Цель:
Проверка соответствия результатов для моделей разных размерностей.
Литература:
M. Courtand et P. Lebelle, Formulaire du beton arme, t.2, Paris, Eyrolles,1976, p. 382.
Формулировка задачи:
Определить перемещение свободного конца x, y, z и максимальное напряжение в защемленном сечении σz .
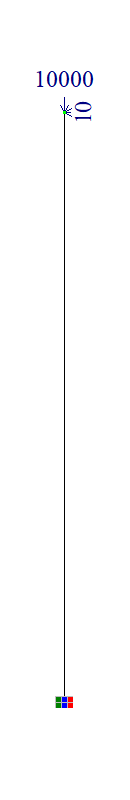
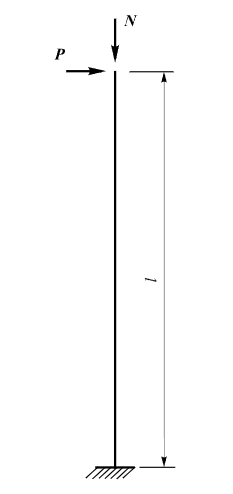
Стержневая модель
|
Оболочечная модель
|
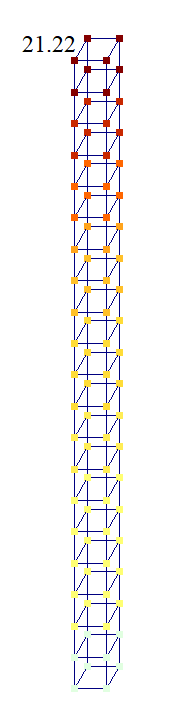
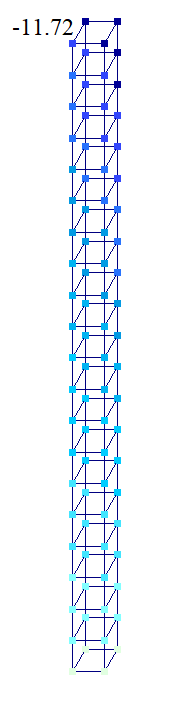
Объемная модель
|
Геометрия:
Высота консольного стержня l = 10 м;
Размеры поперечного сечения консольного стержня b = h = 0,5 м
Характеристика материала:
Модуль упругости Е = 3 * 107 кПа;
Коэффициент Пуассона μ = 0,2
Нагрузки:
Значение сосредоточенной силы, которая действует вдоль оси X общей системы координат Px = 10 кН;
Значение сосредоточенной силы, которая действует вдоль оси X общей системы координат Py = 10 кН
Примечание:
Расчетная схема – система общего вида.
Рассматриваются три расчетные модели: Стeржневая модель, 2 элементы, тип 5, 3 узлы; Оболочечная модель, 20 элементов, тип 50, 85 узлов; Объемная модель, 10 элементов, тип 37, 128 узлов.
Результаты расчета:
|
|
|
|
Значение перемещения x, y, z в стержневой модели (мм)
|
||
|
|
|
|
Значение перемещения x, y, z в пластинчатой модели (мм)
|
||
|
|
|
|
Значение перемещения x, y, z в стержневой модели (мм)
|
||
Сравнение результатов расчета:
| Модель | Загружение 1 | ||||
|---|---|---|---|---|---|
| Перемещение x, y, z (мм) | Погрешность, % | Напряжение σz (кПа) | Погрешность, % | ||
| Стержневая | -21,3 | 0 | 21,3 | 0 | |
| Оболочечная | 21,3 | 0 | 0.06 | - | |
| Объемная | 21,22 | 0 | 0 | -0.6945 | |
| Аналитическое решение | 21,333 | - | 0 | - | |
| Модель | Загружение 2 | ||||
|---|---|---|---|---|---|
| Перемещение x, y, z (мм) | Погрешность, % | Напряжение σz (кПа) | Погрешность, % | ||
| Стержневая | -21,3 | 0 | 21,3 | 0 | |
| Оболочечная | 21,3 | 0 | 0.06 | - | |
| Объемная | 21,22 | 0 | 0 | -0.6945 | |
| Аналитическое решение | 21,333 | - | 0 | - | |
| Модель | Загружение 3 | ||||
|---|---|---|---|---|---|
| Перемещение x, y, z (мм) | Погрешность, % | Напряжение σz (кПа) | Погрешность, % | ||
| Стержневая | -13,3 | 0 | - | - | |
| Оболочечная | -13,3 | 0 | - | - | |
| Объемная | -11,7 | - | - | - | |
| Аналитическое решение | -13,3 | - | - | - | |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
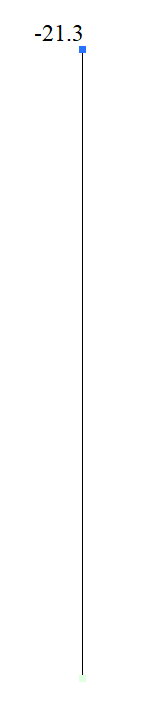
Комментарии