Цель:
Определение напряженного состояния в элементах пространственной шарнирно-стержневой системы под действием сосредоточенной силы.
Литература:
F. P. Beer, E. R. Johnston Jr., D. F. Mazurek, P. J. Cornwell, E. R. Eisenberg, Vector Mechanics for Engineers, Statics and Dynamics, New York, McGraw-Hill Co., 1962, p. 47.
Формулировка задачи:
Определить продольные усилия N в каждом стержне.
:
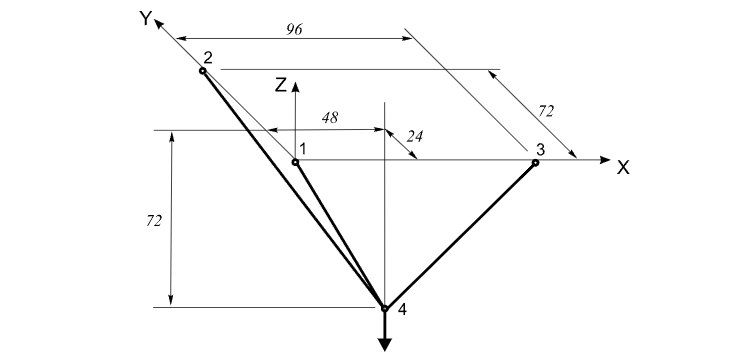
Три стержня пространственной системы соединены в общем узле (4) и шарнирно закреплены в противоположных узлах (1, 2, 3).
|
|
|
|
Начальная геометрия аналитической схемы
|
Начальная геометрия КЭ модели
|
Геометрия:
Площадь поперечного сечения стержней ААС = 1,0 м2
Характеристика материала:
Модуль упругости Е = 3,0 * 107 Па;
Нагрузки:
Вертикальная сосредоточенная сила: F = 0,05 кН.
Примечание:
Расчетная схема — пространственная шарнирно-стержневая система, 3 стержневых элемента типа 4.
Обеспечение граничных условий в опорных узлах достигается путем наложения связей по направлениям степеней свободы: X, Y, Z. Количество узлов в расчетной схеме — 4.
Результаты расчета:
|
|
|
|
Расчетная и деформированная схема фермы
|
Эпюра продольных сил N (Н)
|
Аналитическое решение:
При аналитическом решении продольные усилия N в элементах пространственной шарнирно-стержневой системы при воздействии вертикальной сосредоточенной нагрузки определяются по следующим формулам:
Сравнение результатов расчета:
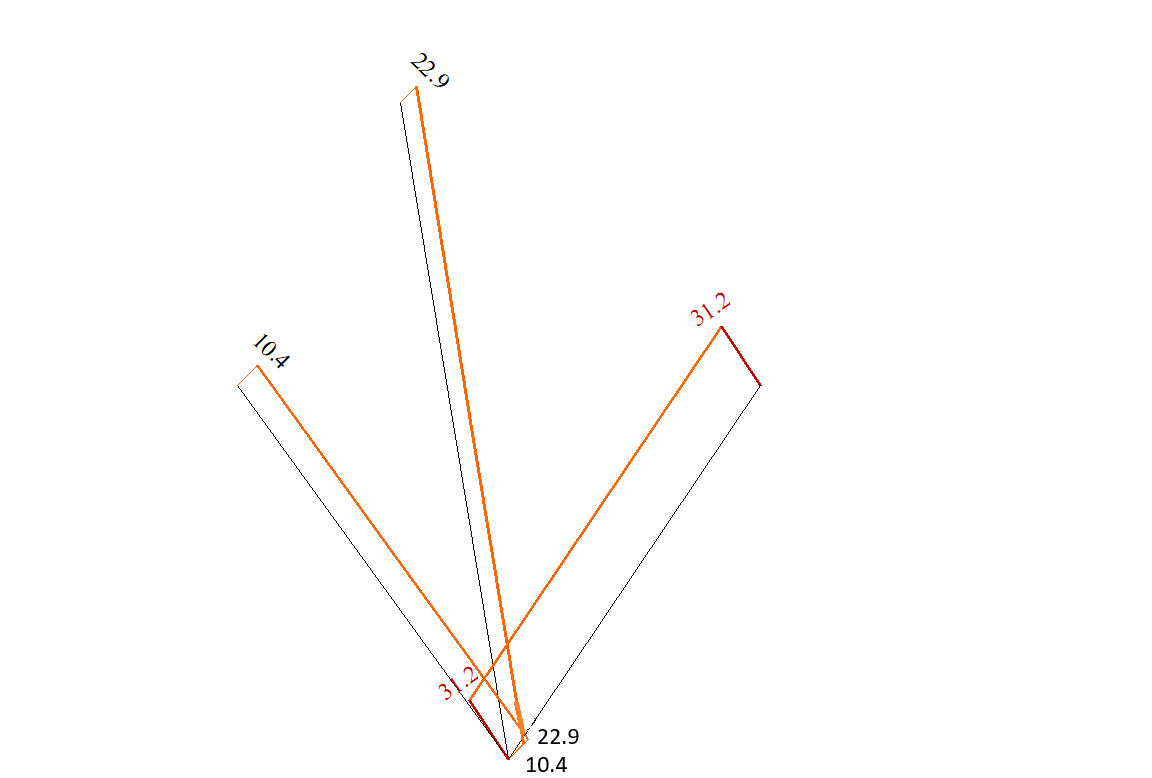
Значения продольных сил N (Н)
| Стержень(узлы) | Аналитическое решение | LIRA-FEM | Погрешность, % |
| 1 (1-4) | 10,39 | 10,4 | 0,1 |
| 2 (2-4) | 22,91 | 22,9 | 0,04 |
| 3 (3-4) | 31,18 | 31,2 | 0,06 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.
Комментарии