Цель:
Определение напряженного состояния симметричного клина единичной толщины при сжатии и изгибе сосредоточенными силами.
Литература:
Демидов С.П. Теория упругости, М., Высшая школа, 1979.
Формулировка задачи:
Определить радиальное напряжение σrr в полярных координатах на расстоянии r = 5 м от вершины клина.
Описание расчетной схемы:
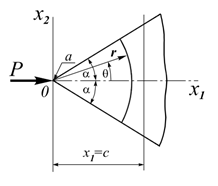
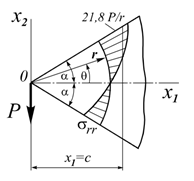
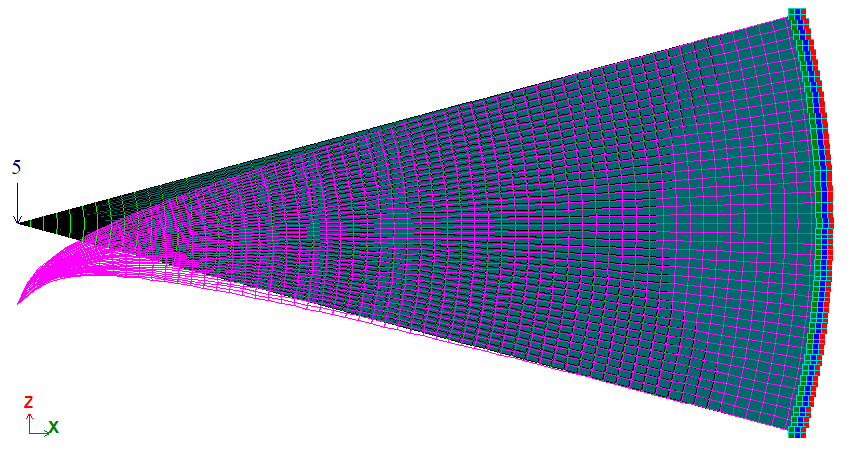
К вершине клина единичной толщины приложена сила Р, которая действует:
Вариант 1: вдоль оси симметрии клина;
Вариант 2: перпендикулярно оси симметрии клина.
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
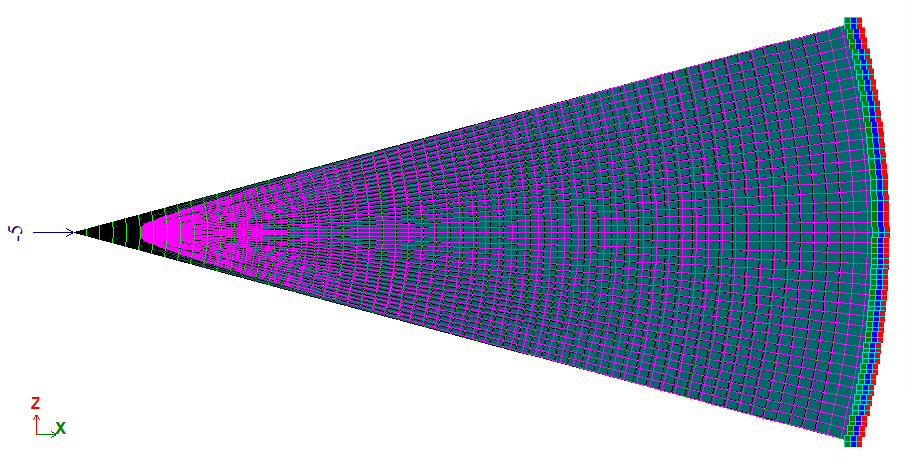
Геометрия:
Толщина клину h = 1 м;
Радиус, ограничивающий область клина, R = 15 м;
Угол при вершине клина 2α = 30°.
Характеристика материала:
Модуль упругости Е = 3 * 107 кПа;
Коэффициент Пуассона ν = 0,2.
Граничные условия:
Связи по всем степеням свободы по контуру дуги клина.
Нагрузки:
Сосредоточенная сила: Р = 5 кН.
Примечание:
Задача решается в пространственной постановке (признак схемы 5).
Для построения схемы использованы КЭ 44 – универсальный четырехугольный КЭ оболочки и КЭ 42 – универсальный треугольный КЭ оболочки.
Сетка конечных элементов имеет 60 элементов вдоль радиуса и 40 вдоль окружности.
Местные оси пластин для результатов согласованы таким образом, что каждая местная ось Y1 направлена в центр окружности.
Количество узлов: 2461. Количество элементов: 2400.
Результаты расчета:
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
Аналитическое решение:
Вариант 1:
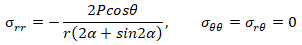
Вариант 2:
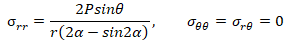
Сравнение результатов расчета:
Без дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % | |
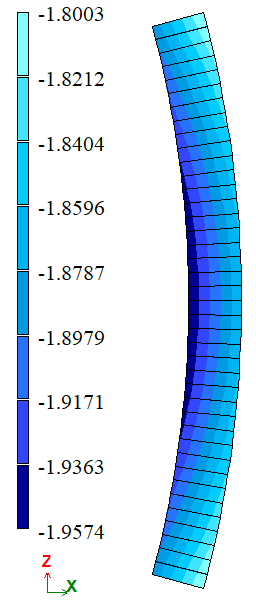
| r = 5 м | Вар. 1 | σrr.max, кН/м2 | -1,88 | -1,8003 | 4,2394 |
| σrr.min, кН/м2 | -1,95 | -1,9574 | 0,3781 | ||
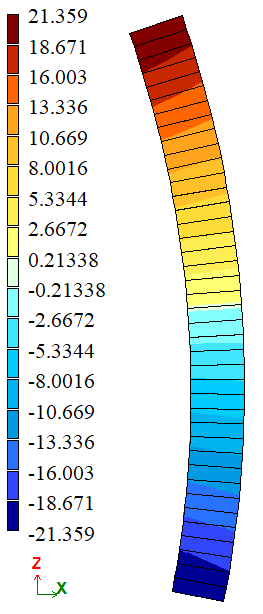
| Вар. 2 | σrr.max, кН/м2 | 21,8 | 21,359 | 2,0229 | |
| σrr.min, кН/м2 | -21,8 | -21,359 | 2,0229 | ||
С использованием дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % | |
| r = 5 м | Вар. 1 | σrr.max, кН/м2 | -1,88 | -1,8006 | 4,2234 |
| σrr.min, кН/м2 | -1,95 | -1,9578 | 0,3984 | ||
| Вар. 2 | σrr.max, кН/м2 | 21,8 | 21,442 | 1,6422 | |
| σrr.min, кН/м2 | -21,8 | -21,442 | 1,6422 | ||
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.


Комментарии