Цель:
Определение напряженно деформированного состояния вертикальной призмы под действием нагрузки от собственного веса.
Литература:
С.П. Тимошенко, Дж. Гудьер. Теория упругости, М., Наука, 1975, С. 289-291.
Формулировка задачи:
ФормуОпределить вертикальные перемещения Z(w) точек B, C, горизонтальное перемещение X(u) точки D, а также напряжения возле верхней грани и в середине высоты стержня.лировка задачи
Описание расчетной схемы:
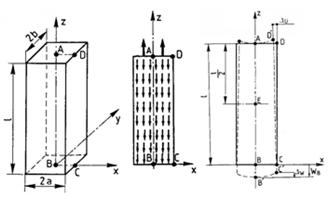
Вертикальный призматический стержень, загруженный собственным весом и нагрузкой возле верхней грани, равной весу стержня.
|
Вариант 1 |
Вариант 2 |
Геометрия:
Длина L = 3 м;
Размеры поперечного сечения a = b = 0,5 м.
Характеристика материала:
Модуль упругости Е = 2 * 107 тс/м2;
Коэффициент Пуассона ν = 0,3.
Объемный вес R0 (ρg) = 7,8 тс/м3.
Граничные условия:
точка А закреплена по Z(Z(wA)=0, чтобы избежать геометрического изменения), по плоскости обреза XZ назначены связи по оси Y(v=0), по плоскости обреза YZ назначены связи по оси X (u=0).
Нагрузки:
собственный вес на призму (действует вниз), на верхнюю грань призмы приложена равномерно распределенная нагрузка равная в сумме объемному весу призмы (действует вверх).
Примечание:
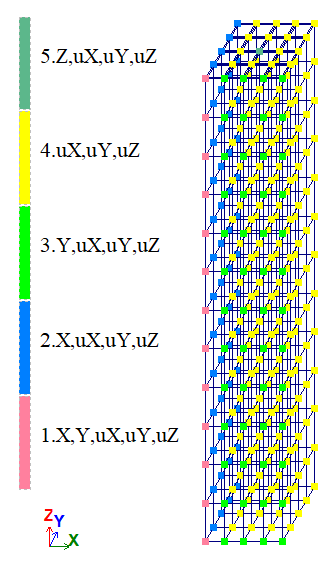
Задача решается в пространственной постановке (признак схемы 5).
Для построения схемы использованы КЭ 31 – параллелепипед.
У розрахунковій схемі розглядається чверть призми, на площинах обрізу призначені в'язі симетрії.
Для прикладання навантаження до верхньої грані призми використовувалися КЭ 11 пластини з Е=0, ν = 0.
Вариант 1:
Сетка 4×4×12.
Количество узлов: 325. Количество элементов: 208.
Вариант 2:
Сетка 8×8×24.
Количество узлов: 2025. Количество элементов: 1600.
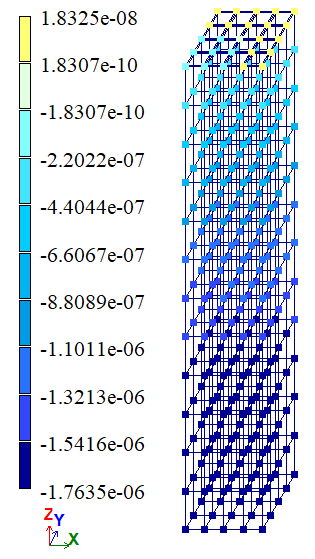
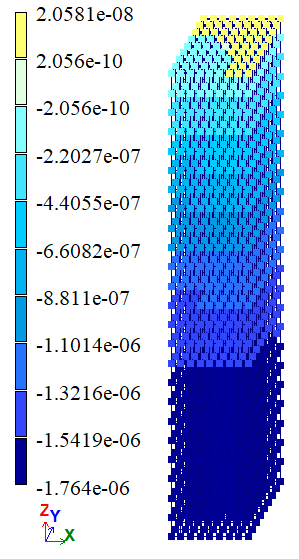
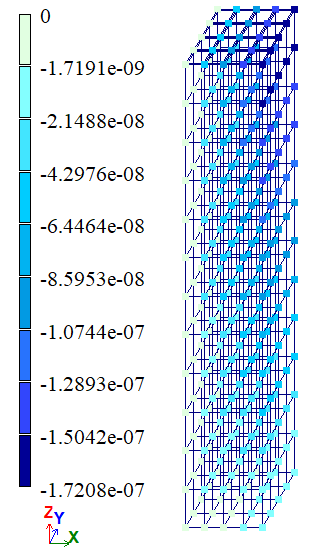
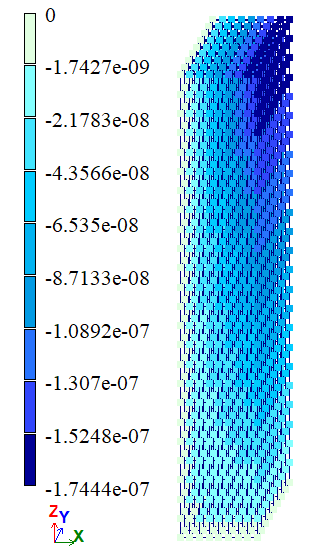
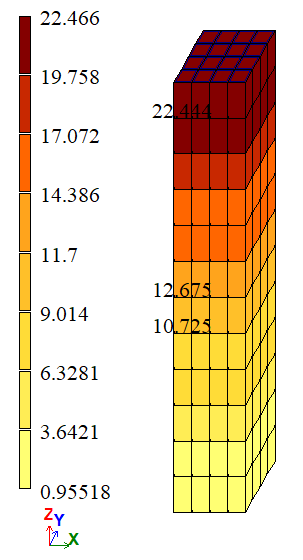
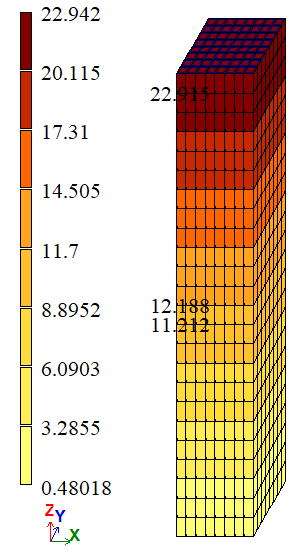
Результаты расчета:
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
|
Вариант 1 |
Вариант 2 |
Аналитическое решение:
σzz = ρgz
σxx = σyy = σxy = σyx = σzx = 0
u = -νρgxz/E

Сравнение результатов расчета:
Без дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % | ||
| Вариант 1 | Вариант 2 | Вариант 1 | Вариант 2 | |||
| В | w (Δz), м | -1,755*106 | -1,755*106 | -1,755*106 | 0 | 0 |
| С | w (Δz), м | -1,74*106 | -1,7584*106 | -1,7447*106 | 1,0464 | 0,2694 |
| D | u (Δx), м | -1,755*107 | -1,7182*107 | -1,7418*107 | 2,0969 | 0,7521 |
| А | σZZ, тс/м2 | 23,4 | 22,444 | 22,9148 | 4,0855 | 2,0735 |
| Е | σZZ, тс/м2 | 11,7 | 11,7 | 11,7 | 0 | 0 |
С использованием дополнительных узлов по сторонам:
| Точка | Искомая величина | Аналитическое решение | LIRA-FEM | Погрешность, % | ||
| Вариант 1 | Вариант 2 | Вариант 1 | Вариант 2 | |||
| В | w (Δz), м | -1,755*106 | -1,7547*106 | -1,7549*106 | 0,0171 | 0,0057 |
| С | w (Δz), м | -1,74*106 | -1,7437*106 | -1,7439*106 | 0,2122 | 0,2236 |
| D | u (Δx), м | -1,755*107 | -1,7533*107 | -1,7545*107 | 0,0969 | 0,0285 |
| А | σZZ, тс/м2 | 23,4 | 22,444 | 22,9226 | 4,0855 | 2,0402 |
| Е | σZZ, тс/м2 | 11,7 | 11,7 | 11,7 | 0 | 0 |
Скачать пример
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Комментарии