Принцип "Определяющее нагружение"

Современные программные комплексы позволяют проводить компьютерное моделирование процессов жизненного цикла конструкций - процессов нагружения, процессов возведения, процессов динамического воздействия, различных форс-мажорных ситуаций и др.

На рис.1 приведена структурная методологическая схема моделирования строительного объекта с учетом всех процессов изменения напряженно-деформированного состояния конструкций на каждой стадии.

Стадии монтажа соответствуют последовательности возведения конструкции, каждая из которых «хранит» историю нагружения. Стадии последовательно сменяют друг друга, соответственно возведенная конструкция на каждой стадии имеет измененное НДС. Последняя MC_k стадия соответствует возведенной конструкции, и ее НДС «хранит» всю информацию последовательности возведения, связанную с изменениями конструктивной схемы, добавлением и снятием монтажных нагрузок и т.п.

Стадия МС_k является стартовой для расчета на эксплуатационные нагрузки. НДС на эксплуатационных стадиях определяется расчетом на различные сочетания нагружений (РСН₁ – эксплуатационные статические нагрузки; РСН₂ – полезные нагрузки с учетом пульсационной ветровой составляющей, РСН₂ – полезные нагрузки с учетом сейсмического воздействия и т.д.). Некоторые эксплуатационные стадии в свою очередь являются стартовыми для моделирования форс-мажорных ситуаций.

Конечно, такое моделирование, даже с учетом все возрастающих возможностей современных компьютеров, является громоздким помимо большого количества расчетов различных конструктивных схем, каждый из них, как правило, надо проводить с учетом геометрической, физической, конструктивной, генетической нелинейности. Особенно это касается форс-мажорных ситуаций, когда необходимо определять дополнительные резервы несущей способности конструкции с целью не допустить прогрессирующего обрушения при минимальных дополнительных расходах материалов. Кроме того, определение НДС конструкции на эксплуатационных стадиях должно учитывать временные изменения реологических свойств материала (усадка, ползучесть и др.), что также обуславливает необходимость проведения расчета в нелинейной постановке [4].

Проведение такого расчета все-таки является достаточно громоздким и в настоящее время применяется только при проектировании уникальных объектов не имеющих аналогов. Как правило подавляющее большинство расчетов проводят по традиционной схеме (рис.2)

Расчет в линейной постановке не учитывает ряд важных факторов, например, физическую нелинейность железобетона. Этот фактор обуславливает не только значительное увеличение перемещений (в 2-3 раза по сравнению с расчетом в нелинейной постановке), но и перераспределение усилий, что адекватно отображает действительную работу конструкций.

Принцип «определяющее нагружение» с одной стороны реализует учет различных факторов, недоступных при расчете в линейной постановке, с другой стороны сохраняет традиционную технологию расчета (рис.2).

Пример принципа «Определяющее нагружение» в методике «Инженерная нелинейность»

Пример применения принципа «Определяющее нагружение» при назначении коэффициентов постели

Величины коэффициентов постели зависят от глубины сжимаемой толщи, которая в свою очередь зависит от нагрузки. Таким образом это обуславливает нелинейную постановку задачи.

Пример принципа «Определяющее нагружение» позволяет провести расчет по следующей схеме:

1. Предварительно назначаем равномерное напряжение под подошвой фундамента, путем деления массы здания на площадь фундамента (шаг 1, рис.9). Получаем переменные коэффициенты постели по площади фундамента от равномерного напряжения под подошвой. Прикладываем отпор грунта от выбранного определяющего нагружения (шаг 2-4, рис.9).
2. Определяем коэффициенты постели для каждого конечного элемента фундаментной конструкции от неравномерного напряжения под подошвой фундамента (шаг 5, рис.9).
3. Расчет по традиционной схеме на все нагружения с учетом найденных в. п 2 коэффициентов постели.

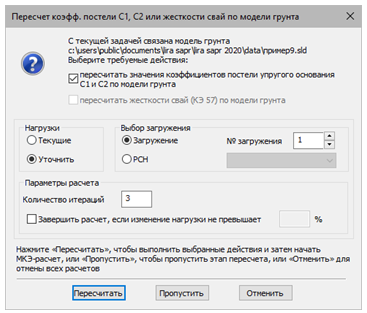
При моделировании свайных фундаментов в ПК ЛИРА-САПР есть возможность уточнять нагрузки на оголовки свай для пересчета жесткостей (жесткости меняются с учетом взаимовлияния осадок в группе свай, поскольку поменялись нагрузки на оголовки соседних свай). Начиная с версии ЛИРА-САПР 2019, реализован инструмент для автоматизации выполнения итерационных расчетов (без участия пользователя) (рис.10).

Применение принципа «Определяющее нагружение» при назначении размеров полок для балочного ростверка

Усиление плит балками достаточно часто встречается в современном домостроении. Расположение балок, как правило, нерегулярное, нет четко выраженной системы главных и второстепенных балок, балки могут иметь небольшую высоту, и здесь часто нагрузки передаются на опоры за счет работы как собственно плиты, так и за счет балок.

В этом случае опыт расчета и проектирования ребристых перекрытий (эти примеры имеются в каждом учебнике по железобетонным конструкциям, где рекомендуется собирать нагрузку с плиты на второстепенные балки, считая опирание плиты на них жестким, затем рассчитать второстепенные балки, считая их опирания на главные балки жестким и т. д.) малопригоден и может иметь разве что антикварную ценность.

С другой стороны, с точки зрения метода конечных элементов как будто бы не должно быть никаких проблем: вводится конечно-элементная сетка плиты с базовыми точками на линиях балок, нагрузка прикладывается по верху плиты и т. д. Но здесь возникает много проблем, связанных со стыковкой в конечно-элементной модели элементов различной мерности. Главная проблема здесь - как назначить жесткость балки.

Если в конечно-элементную модель плиты, узлы сетки которой лежат на срединной поверхности, ввести стержни сечением h_сxb_с, то будет рассчитана система с взаимным расположением плиты и балки, представленным на рис.11б. Конечно, такая модель не выдерживает никакой критики. Можно ввести тавровое сечение балки. Взаимное расположение плиты и балки в этом случае представлено на рис.11в. Но здесь возникает вопрос о том, как назначить ширину полки. Разные методические материалы дают различные рекомендации - от 6 до 15 толщин плиты. Кроме того, по этой схеме работа плиты учитывается дважды. Правда, это вполне допустимо, так как конечные элементы плиты моделируют изгибную группу усилий, а часть плиты в составе полки балки моделирует мембранную группу усилий, которая вызывает в плите небольшие напряжения по сравнению с напряжениями от изгибной группы. Достаточно адекватной является модель, предложенная в [10], где взаимодействие плиты и балки представлено на рис.11г.

В этом случае стержни сечением h_сxb_с, подвешиваются при помощи абсолютно жестких вставок к узлам конечно-элементной модели плиты, лежащими в ее срединной поверхности. Здесь (в отличие от моделей рис. 11б и рис. 11в, где в конечных элементах плиты и стержней возникает только изгибная группа усилий, а каждый узел конечно-элементной схемы имеет три узловых неизвестных - вертикальное перемещение и два угла поворота) каждый узел конечно-элементной схемы имеет пять узловых неизвестных – три линейных перемещения и два угла поворота, а конечные элементы плиты испытывают кроме изгибной также мембранную группу усилий, а в стержневом элементе, кроме изгибающего момента (М_с) и поперечной силы, возникает еще и нормальная сила (N_с).

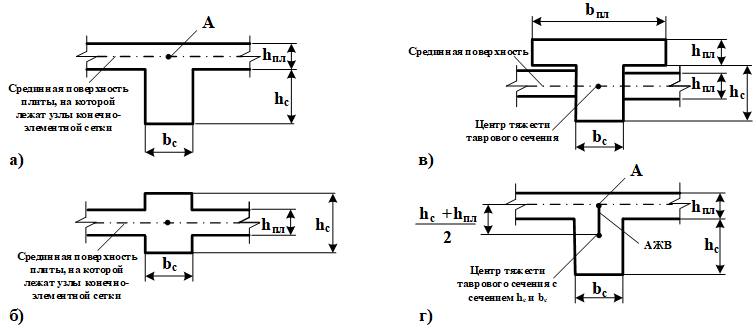
Хотя последняя модель и наиболее полно отображает действительную работу конструкции, и снимают вопрос о назначении ширины полки в тавровой балке, вместе с тем на последних этапах проектирования балки возникают трудности. Конечно, можно просто рассчитать сечение стержня h_сxb_с, на полученные в нем усилия М_c, и N_c. Однако, как правило, значение N_c велико, и сечение будет законструировано как внецентренно растянутый элемент, а подобранная арматура в нем будет распределена по всему периметру, в то время как по правилам конструирования балочных ростверков арматура должна быть расположена у нижней и верхней грани. Таким образом, для конструирования желательно рассматривать тавровое сечение балки, подверженное изгибу, однако неясно, какой изгибающий момент действует на балку и какое сечение балки надо рассчитывать. В этом случае можно рассматривать следующий инженерный подход, основанный на гипотезе о том, что равнодействующая мембранных сил плиты, уравновешивающих нормальную силу в подвешенном стержне (N_с), приложена в центре плиты (точка А рис.12а). Тогда можно считать, что изгибающий момент, действующий на балку таврового сечения, равен М_б=М_с+N_сх0,5(h_с+h_n). Остается только определить ширину полки тавровой балки. Здесь можно с некоторой натяжкой использовать выше принятую гипотезу: если центр тяжести мембранных сил приложен в центре плитной части (точка А), то полка должна быть равномерно сжата. Так как арматура будет рассчитываться в рамках предположений о предельном состоянии сечения, то напряжение в полке будет R_б. Поэтому ширина полки b<_n = N_c/(h_nR_б).

Поперечная сила в балке определяется как первая производная (при численных расчетах используется конечноразностный подход) от моментов М_б(х). Так как эпюры М_с и N_с в стержне имеют ступенчатый вид, т. е. в каждом сечении имеется два значения момента и нормальной силы, то их следует либо усреднить, либо брать их значения в серединах отрезков. Конечно, предположения о том, что напряжения в полке для определения М_б, приняты постоянными, а при определении b_n, равны R_б, в ряде случаев могут оказаться недостаточно удачными, поэтому ниже приводится несколько другой подход, основанный на гипотезе плоских сечений (рис.12б). Деформация сечения определяется на основе эпюры напряжений в сечении стержня:

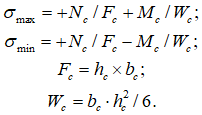
Далее наклон сечения продлевается в область плиты и из геометрических соотношений определяется .

После этого определение М_б и b_n представляется делом техники:

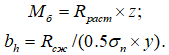
В данном случае принцип «определяющее нагружение» позволяет провести расчет по следующей схеме.

1. Назначение определяющего нагружения.
2. Определение ширины полки по вышеуказанной методике для каждого участка балочного ростверка.
3. Расчет балочного ростверка на все нагружения с назначенными по п 2. размерами полок.

Вывод: Рассмотренные примеры применения принципа «определяющее нагружение», по-видимому не исчерпывают все области его применения. Инженерная практика будет подсказывать эти области, которые и будут реализовываться в ПК ЛИРА-САПР.

Литература

1. Барабаш М. С. Влияние процесса возведения на пространственную работу несущих систем зданий / М. С. Барабаш // Строительство, материаловедение, машиностроение // Сб. научн. Трудов. – Дн-вск: ПГАСА, 2012. – № 65. – С. 29 - 34.
2. Барабаш М. С. Компьютерное моделирование процессов жизненного цикла объектов строительства: Монография / Мария Сергеевна Барабаш. – К.: «Сталь», 2014. – 301 с
3. Бондаренко В. М. Инженерные методы нелинейной теории железобетона / В.М. Бондаренко – М.: Стройиздат, 1982. – 287 с.
4. Городецкий А. С. Компьютерные модели конструкций / А. С. Городецкий, И. Д. Евзеров. – [2-е изд., доп.] – Киев: "ФАКТ", 2007. – 394 с.
5. Городецкий А. С., Барабаш М. С. Компьютерное моделирование процесса возведения строительных конструкций / А. С. Городецкий, М. С. Барабаш // Строительная механика и расчет сооружений: Научно-технический журнал. – Москва: ЦНИИСК им. В. А. Кучеренко, 2014. – Вып. 5 (256). – С. 28–33.
6. Городецкий А.С., Барабаш М.С., Сидоров В.Н. Компьютерное моделирование в задачах строительной механики Учебное пособие. / А. С. Городецкий, М. С. Барабаш, В. Н. Сидоров – М.: Издательство АСВ, 2016. – 338 с.
7. Городецкий А. С. К расчету физически нелинейных плоских рамных систем /А. С. Городецкий, В. С. Здоренко // Строительная механика и расчет сооружений. – 1969. – № 4. – С. 61-68.
8. Городецкий А. С. Компьютерное моделирование процесса нагружения железобетонных конструкций. Сборник научных трудов Луганского национального университета, серия «Технические науки» N49/52, - Л.: Из-во «ЛНАУ», 2004, с.3-10.
9. Городецкий А. С. Учет нелинейной работы железобетонных конструкций в практических расчетах / А. С. Городецкий, М. С. Барабаш // Строительство, материаловедение, машиностроение // Сб. научн. Трудов. – Дн-вск: ПГАСА, 2014. – Вып. 77. – С. 54–59.
10. Метод конечных элементов: теория и численная реализация / [Городецкий А. С., Евзеров И. Д., Стрелец-Стрелецкий Е. Б. и др.]. – К. : Факт, 1997. – 138 с. – (Программный комплекс ЛИРА-Windows).
11. Пикуль А. В. Определение жесткостных характеристик сечения железобетонного стержня с учетом нелинейных свойств материала / А.В. Пикуль, Д.А. Городецкий // Актуальные проблемы компьютерного моделирования конструкций и сооружений: тезисы докладов IV Международного симпозиума. – Челябинск.: Издательский центр ЮУрГУ, 2012. – С. 228.