
Тепло самопроизвольно переносится только в сторону убывания температуры. Количество тепла, переносимое через какую-либо изотермическую поверхность в единицу времени, называется тепловым потоком Q [1].
В стационарных процессах теплопроводности температура в любой точке твердого тела не зависит от времени, иначе 𝜕𝑡/𝜕𝜏=0.
В условиях стационарного теплового состояния плоского тела тепловой поток описывается законом Фурье:
![]() (1)
(1)
где Q - const для любой координаты х;
dt/dx – градиент температуры;
F(x) - поверхность тела, соответствующая координате х;
λ - коэффициент пропорциональности, называемый коэффициентом теплопроводности.
Аналогичное уравнение можно записать для цилиндрического тела, заменив координату х на r:
![]() (2)
(2)
Интенсивность процесса стационарной теплопроводности оценивают с помощью плотности теплового потока.
Тепловой поток, отнесенный к единице площади изотермической поверхности, называется плотностью теплового потока q.
Плотность теплового потока есть вектор, направление которого совпадает с направлением распространения тепла в данной точке и противоположно направлению вектора температурного градиента (рис. 1) [1].

В случае плоской стенки, когда внутренняя и наружная ее поверхности равны, плотность теплового потока равна (Вт/м2= Дж/(c·м2)):
![]() (3)
(3)
В случае цилиндрической стенки ее поверхность по мере удаления от оси увеличивается, а плотность теплового потока уменьшается. Поэтому для оценки интенсивности теплопроводности через цилиндрическую стенку используют понятие плотности теплового потока на погонный метр (Вт/м= Дж/(c·м)):
![]() (4)
(4)
где, 1 - длина, r - радиус цилиндрической стенки, м.
Тест 2 Стационарное распространение тепла в пластине (сечение кольцо) при граничных условиях первого рода (заданная температура)
Тест 3 Стационарное распространение тепла в пластине (сечение кольцо) при смешанных граничных условиях первого и третьего рода (заданная температура и конвекция)
При стационарном тепловом состоянии плоской стенки тепловой поток через нее постоянный. Поэтому, проинтегрировав уравнение (3), приняв при этом λ = const, получим для однослойной стенки следующее выражение (Вт/м2= Дж/(c·м2)):
![]() (5)
(5)
где t1 и t2 - температура соответственно на внутренней и наружной поверхностях стенки, 0С;
S - толщина стенки, м.
Тест 7 Стационарное распространение тепла в стержне при граничных условиях третьего рода (конвекция)
Если плоская стенка имеет n слоев, то плотность теплового потока через нее можно выразить следующим образом (Вт/м2= Дж/(c·м2)):
![]() (6)
(6)
В этом случае каждый слой имеет свои толщину Si и коэффициент теплопроводности λi. Отношение S/λ называют термическим сопротивлением слоя.
Тест 8 Стационарное распространение тепла в неоднородном стержне при граничных условиях третьего рода (конвекция)
Тест 11 Стационарное распространение тепла по радиусу полого шара при граничных условиях третьего рода (конвекция)
Тест 12 Стационарное распространение тепла по радиусу неоднородного полого шара при граничных условиях третьего рода (конвекция)
Для определения теплового потока, проходящего через стенку при стационарном тепловом состоянии, необходимо его плотность q умножить на поверхность плоской стенки, т.е.:
![]() (7)
(7)
Пример расчета
Определить тепловой поток Q (Дж/c), проходящий через плоскую двухслойную стенку, имеющую поверхность F = 12 м2, а так же найти температуру на границе слоев, если известно, что стенка состоит из слоя шамота толщиной S1 = 0,46 м и слоя теплоизоляции толщиной S2 = 0,25 м; коэффициенты теплопроводности слоев соответственно λ1 = 0,84 Дж/(м*с*°С) и λ2 = 0,28 Дж/(м*с*°С); температура внутренней поверхности стенки t1 = 1395°С, температура наружной поверхности t3 = 80°С.
Решение
Создаем задачу в 15м признаке схемы - задачи теплопроводности (одна степень свободы в узле – температура t) (рис. 2).
Рассмотрим участок стены, высотой 1 метр. Толщина первого слоя S1 = 0,46 м (слой шамота), толщина второго слоя S2 = 0,25 м (теплоизоляция).
ШАГ 1. Геометрия
Зададим балку-стенку с помощью команды Создание плоских фрагментов и сетей (рис.3).
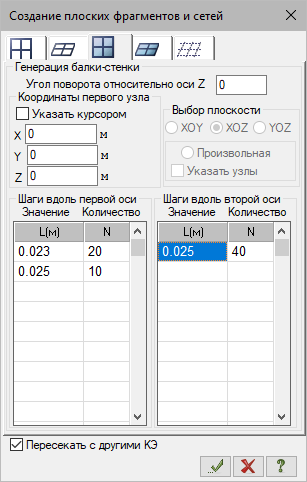
Рис.3. Формирование геометрии (диалоговое окно Создание плоских фрагментов и сетей)

В пятнадцатом признаке схемы для 4-х узловых пластин по умолчанию назначается тип КЭ1509 - четырёхугольный конечный элемент теплопроводности.
ШАГ 2. Характеристики материалов
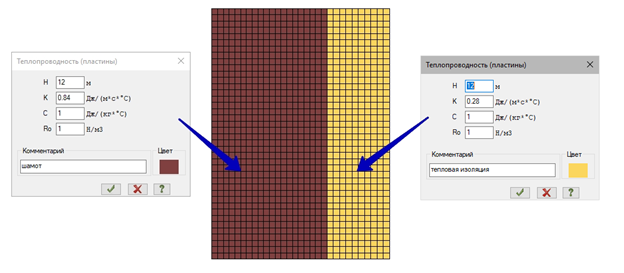
С помощью диалогового окна Жесткости и материалы (рис. 5) создадим набор жесткостей Теплопроводность (пластины), где зададим соответствующие коэффициенты теплопроводности K для слоёв стены. Значения коэффициента теплопоглощения C и удельного веса Ro в задачах стационарной теплопроводности не учитываются, поэтому можно их задать равными единице.

Назначим жесткости на элементы расчетной схемы(рис.6)
ШАГ 3. Внешнее воздействие
Температуру внутренней и наружной поверхности стенки задаем как заданную температуру в узлах. В диалоговом окне Задание нагрузок выбираем закладку Нагрузки в узлах → Заданная температура ![]() , в диалоговом окне Параметры задаем температуру:
, в диалоговом окне Параметры задаем температуру:
- температура внутренней поверхности стенки t1 = 1395°С;
- температура наружной поверхности t3 = 80°С(рис.7).

ШАГ 4. Тепловой поток в узлах
Плотность теплового потока через двухслойную стенку можно определить по формуле (6)
![]() (8)
(8)
Тепловой поток по формуле (7)
![]() (9)
(9)
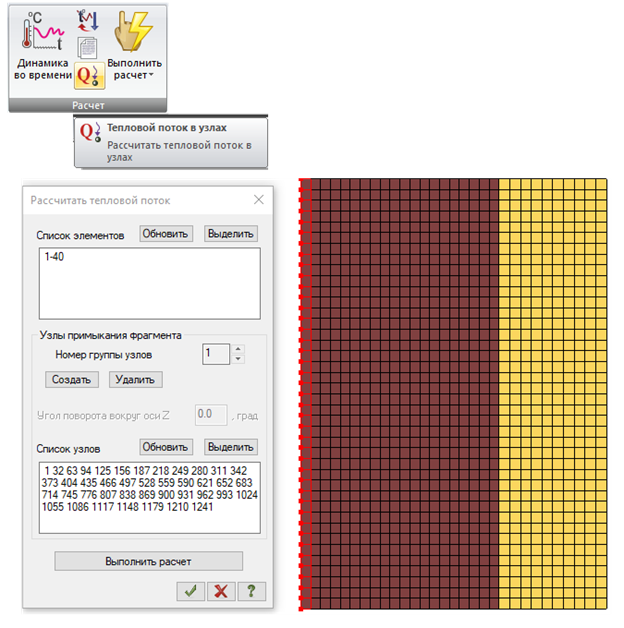
В ПК ЛИРА-САПР в процессе расчета определяется тепловой поток в узлах расчетной схемы от выбранных элементов. Для этого в диалоговом окне Рассчитать тепловой поток (рис.8) необходимо задать следующую информацию:
– номера узлов, в которых должен быть вычислен тепловой поток;
– номера элементов, которые передают тепловой поток в эти узлы.
Списки элементов и узлов можно редактировать вручную, перечислив в соответствующих полях их номера. Если на схеме предварительно выделить элементы и узлы, то составить списки для расчета теплового потока в узлах можно автоматически с помощью кнопок Обновить. В соответствующих полях Список элементов и Список узлов отобразятся перечни номеров только тех элементов/узлов, которые в момент нажатия кнопки отмечены на схеме.
ШАГ 5. Просмотр результатов
Выполняем расчет схемы. Становится доступным просмотр результатов в виде Мозаик теплового потока (рис. 9).

Для определения теплового потока, проходящего через стенку при стационарном тепловом состоянии, необходимо выполнить суммирование теплового потока в узлах. Для этого выделяем узлы, в которых был ране вычислен тепловой поток и в диалоговом окне Суммирование нагрузок нажимаем кнопку Применить (рис.10).
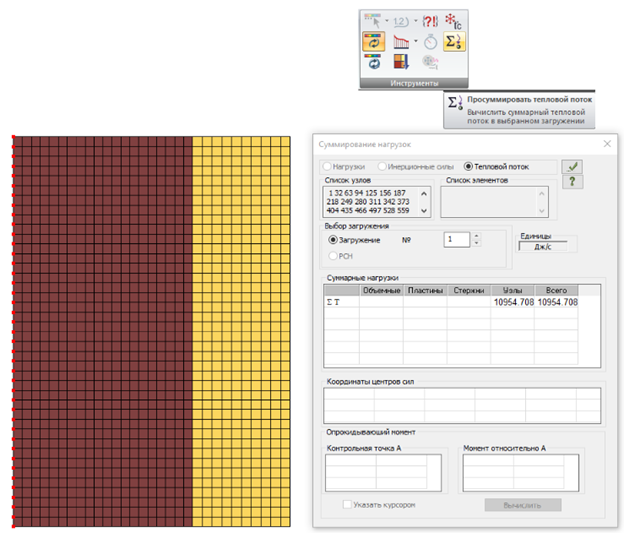
Рис.10. Тепловой потока, проходящего через стенку
Найдем температуру на границе слоев, помня, что тепловой поток через каждый слой есть величина постоянная, т.е.:
![]() (10)
(10)
Из приведенного выше выражения вытекает, что:
![]() (11)
(11)
В ПК ЛИРА-САПР после расчета становится доступным просмотр результатов в виде Изополей температур (рис.11).
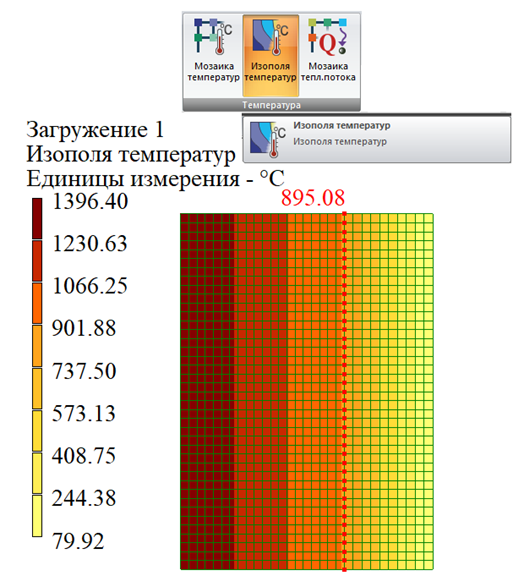
Рис.11. Температура на границе слоев стенки
Определение суммы тепловых потоков Пример
- Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е стереотип. «Энергия», 1977 – 344с.
- Тепловая защита зданий. Актуализированная редакция СНиП 23-02-2003 (с Изменением N 1):СП 50.13330.2012. – [Введен в действие с 07-01-2013 ]. – M.: Минрегион России, 2012. – 100 с. – (Свод правил). (Приложение Н.)
- Проектирование тепловой защиты зданий:СП 23-101-2004. – [Введен в действие с 01-06-2004 ]. – M., 2004. – 145 с. – (Свод правил). (Приложение М.)
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Комментарии