Возможности применения суперэлементов при решении различных задач строительной механики

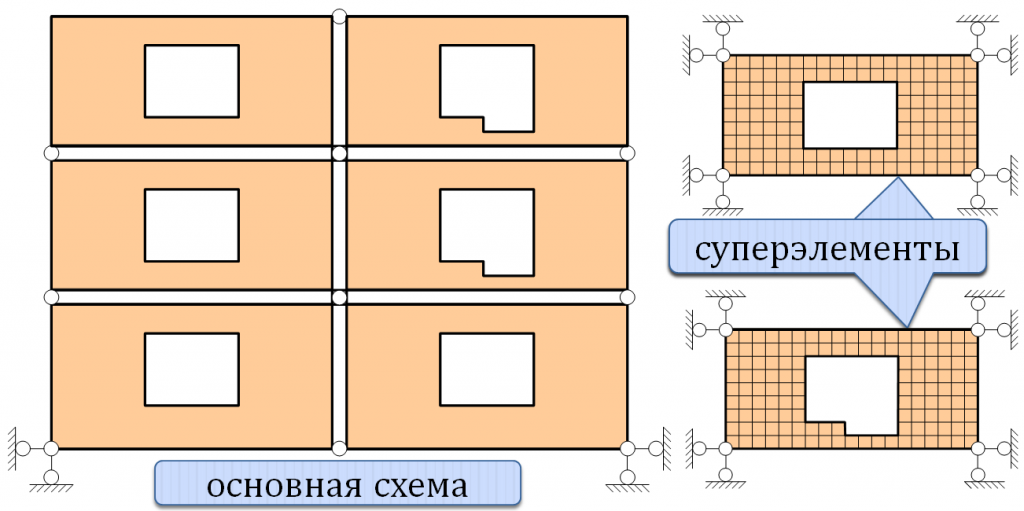
Если рассчитываемая система слишком громоздка, то иногда оказывается удобным организовать рекурсивный расчет с расчленением всей системы на подсистемы - суперэлементы. Этот прием может оказаться удачным, когда расчленение на подсистемы происходит естественно: например, здание из объемных блоков (объемный блок - суперэлемент) или диафрагма высотного здания, собирающаяся из отдельных панелей (панель - суперэлемент). Фрагмент диафрагмы высотного здания показан на рис. 1а. Диафрагма состоит из отдельных панелей, соединяющихся между собой в угловых точках.

Расчет такой системы можно выполнить обычным способом: нанести необходимую сетку   и рассчитать всю систему целиком. Однако большое количество расчетных узлов, элементов, неизвестных перемещений может сильно затруднить решение задачи.

Используя суперэлементы, можно провести расчет поэтапно, существенно снизив на каждом этапе размерность задачи.

Сначала построить матрицу жесткости для всех типов суперэлементов (в данном случае имеются два типа (рис. 1б), затем рассчитать систему, состоящую из суперэлементов (в данном случае система будет состоять из 6 суперэлементов с 12 суперузлами). В результате этого расчета будут определены перемещения суперузлов. На заключительном этапе рассчитать каждый из шести суперэлементов на заданные перемещения суперузлов и местную нагрузку.

Последовательность расчета системы, набранной из суперэлементов, аналогична обыкновенной процедуре МКЭ с той лишь разницей, что матрица жесткости и приведение местной нагрузки к узловой определяются не на основе аппроксимирующих функций МКЭ, а численным методом. Так как суперэлемент представляет сам по себе достаточно сложную систему, то матрицы аппроксимирующих функций строятся при помощи численного расчета суперэлемента на единичные смещения суперузлов, в результате которого строится матрица влияния, связывающая перемещения внутренних узлов суперэлемента с единичными смещениями суперузлов. Такая процедура обработки суперэлементов позволяет представить метод суперэлементной рекурсии как расчет по методу конечных элементов с построением аппроксимирующих функций при помощи матриц влияния.

Другая процедура обработки суперэлементов [3], основана на том, что в физическом смысле исключения j неизвестного по Гауссу соответствует освобождению от j связи. Это приводит к такой схеме построения матрицы жесткости и сведение местной нагрузки к узловой: для i суперэлемента вначале нумеруются все внутренние узлы (соответствующее им число степеней свободы обозначим n_i), а затем суперузлы (количество степеней свободы, соответствующее суперузлам, обозначим n_i0); составляются канонические уравнения для всех n_i+n_i0 степеней свободы (риc. 2); исключаются n_i неизвестные; оставшиеся части матрицы и столбцов свободных членов (на рис. 2 они заштрихованы) образуют искомые матрицы жесткости и столбцы узловых нагрузок в суперузлах суперэлемента, к которым приведена местная нагрузка приложенная по области суперэлемента.

Можно построить вычислительный процесс расчленяя суперэлементы на суперэлементы второго ранга и т. д. организовав многоранговую рекурсию МСЭ.

Основные идеи метода суперэлементов (МСЭ) были впервые изложены в работе Пржеминицкого [1]. Идеи Пржеминицкого получили свое развитие в работе Мейснера [2], который придал им формализованный вид и обобщил на несколько уровней разделения (многоранговая рекурсия МСЭ). Дальнейшему развитию МСЭ посвящен ряд более поздних работ [3-12].

Если проводить математические аналогии, то МСЭ отдаленно напоминает блочный Гаусс, а многоранговая рекурсия МСЭ - современный метод вложенных сечений для решения разреженных матриц, однако, как и МКЭ метод суперэлементов основан на непосредственной дискретизации расчетной модели. В этом смысле МСЭ обладает большой наглядностью, он естественен и напоминает процесс сборки конструкции из секций и блоков.

МСЭ очень эффективен в ряде случаев, например:

• при решении большеразмерных задач содержащих одинаковые в смысле топологии суперэлементы. Здесь значительно сокращается количество вычислений, так как матрица жесткости для одинаковых суперэлементов строится только один раз.
  
• при расчете конструктивных схем, где нелинейность локализована в некоторой области.
  
• при построении матрицы жесткости элементов с существенным изменением жесткостных характеристик по области элемента, вызванных либо нелинейностью, либо конструктивными особенностям (стержень с переменным сечением по длине).
  
• при построении матрицы жесткости элементов взаимодействующих с большеразмерной средой и примыкающих к основной конструктивной схеме одним узлом (например, свая в грунтовом массиве).
  

Расчет конструктивной схемы включающей одинаковые суперэлементы

Расчетная схема представлена на рис. 3

Расчет выполнялся программным комплексом ЛИРА-САПР на компьютере Pentium Core i7 (8 ядер), 16 GB.

Было выполнено два расчета (использовались прямоугольные конечные элементы пластин) без применение суперэлементов и с применением суперэлементов.

Расчет схема для первого расчета содержала 3771744 элементов, 3850650 узлов, 19421820 неизвестных. Расчетная схема для второго расчета содержала 378 суперэлементов. Каждый суперэлемент включал 660 узлов.

Сравнение результатов по двум расчетам приведена в табл. 1.

Таблица 1

Приведенный пример демонстрирует значительное увеличение скорости решения задачи (см. табл.1). Этим не исчерпывается преимущества МСЭ – значительно облегчается подготовка исходных данных анализ результатов, но, по-видимому, наиболее важным преимуществом МСЭ является повышение точности решение задачи. При большой размерности задачи и большом разбросе величин жесткостных характеристик ухудшается обусловленность задачи и накапливаются ошибки округления, что в ряде случаев может привести к неправильным результатам. МСЭ в этих случаях является действенным инструментом для борьбы с «проклятием» размерности, которое присуще большинству численным методам включая и МКЭ.

Расчет конструкций с локализованной областью нелинейности

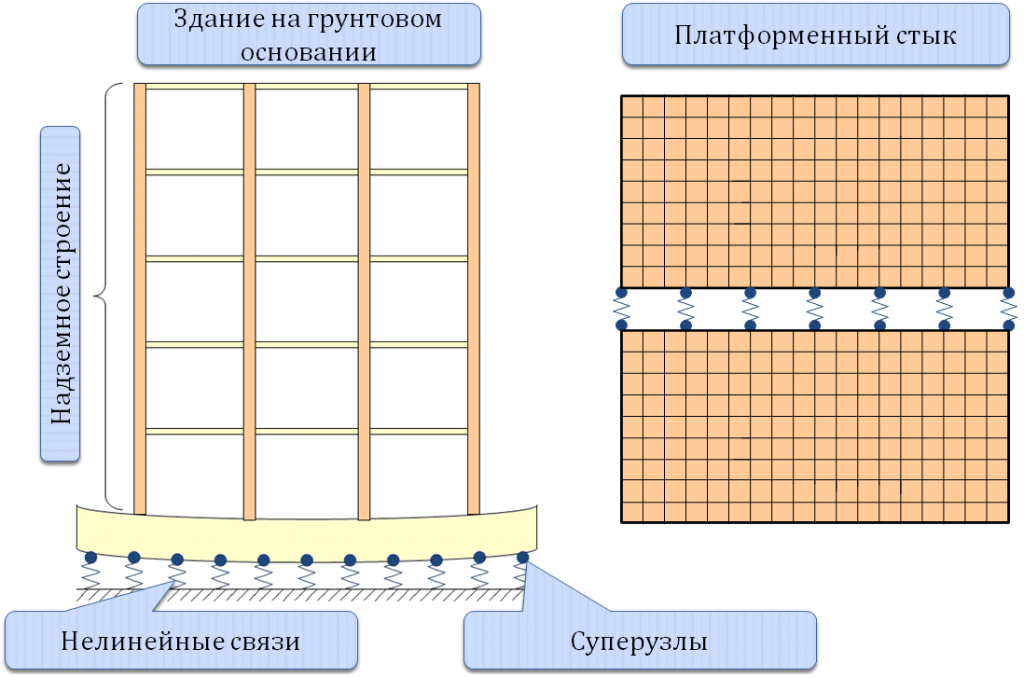
На рис. 4 схематично представлена расчетная схема конструкции, представляющая надземное строение опирающееся на систему связей, обладающих существенной нелинейностью. Само надземное строение в рамках заданной точности может рассчитываться в линейной постановке. Расчетная схема надземного строения может содержать большое количество узлов и элементов и включение ее в нелинейный расчет, обусловленный существенной нелинейностью связей обусловит большое время решения задачи. В этом случае целесообразно объявить расчетную модель надземного строение суперэлементом и решать нелинейную задачу только для основной схемы включающей суперузлы (на рис.4, а обозначены жирными точками) и нелинейные связи.

Такой же прием может быть использован при построении расчетной схемы панельного здания с платформенными стыками панелей (рис. 4, б).

Сборные панели при эксплуатационной нагрузке практически работают в линейно упругой стадии и нелинейность работы всей конструкции сосредотачивается в локальных областях платформенных стыков. Поэтому вводя в расчетную схему панели в виде суперэлементов можно значительно сократить время решения нелинейной задачи.

                                                         а)                                                                                                б)

Применение МКЭ для построения матриц жесткости стержня, имеющее переменное сечение по длине

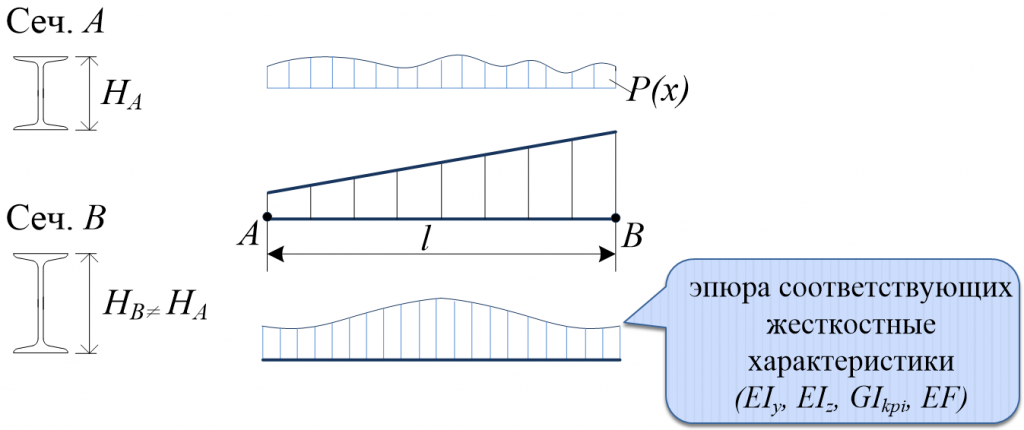
Переменная жесткость по длине стержня сечение может быть обусловлена переменной высотой стенки, или переменными ширинами полок или другими конструктивными особенностями. В этих случаях построение зависимости изменения жесткостных характеристик по длине стержня, с тем чтобы аналитически построить матрицу жесткости, может вызвать значительные трудности, тем более, что эти зависимости для EIz, EIy, EF, GI_кp как правило различны.

Можно ввести в расчетную схему такие стержни с многочисленными промежуточными узлами, однако это приводит к значительному увеличению размера задачи, затрудняет составление исходных данных и анализ результатов. В этом случае удобным оказывается применение МСЭ (рис. 5).

Стержень разбивается по длине на n участков. Узлы А и В объявляются суперузлами. По схеме (рис. 2) производится построение матриц жесткости стержня и приведение местной нагрузки к узловой.

В результате решение всей системы определяется перемещения узлов А и В. В случае необходимости определения перемещений во внутренних узлах элемента выполняется обратный ход для столбцов свободных членов – см. рис. 2, где n_io – найденные перемещения суперузлов А и В, а затем и усилия по длине стержня.

Применение МСЭ для построения матрицы жесткости стержня для нелинейных задач

При решении задач с учетом физической нелинейности важной процедурой является построение матрицы жесткости стержня на m шаге или на n итерации. Изменение усилий по длине стержня обуславливает изменение жесткостных характеристик сечений (рис. 6).

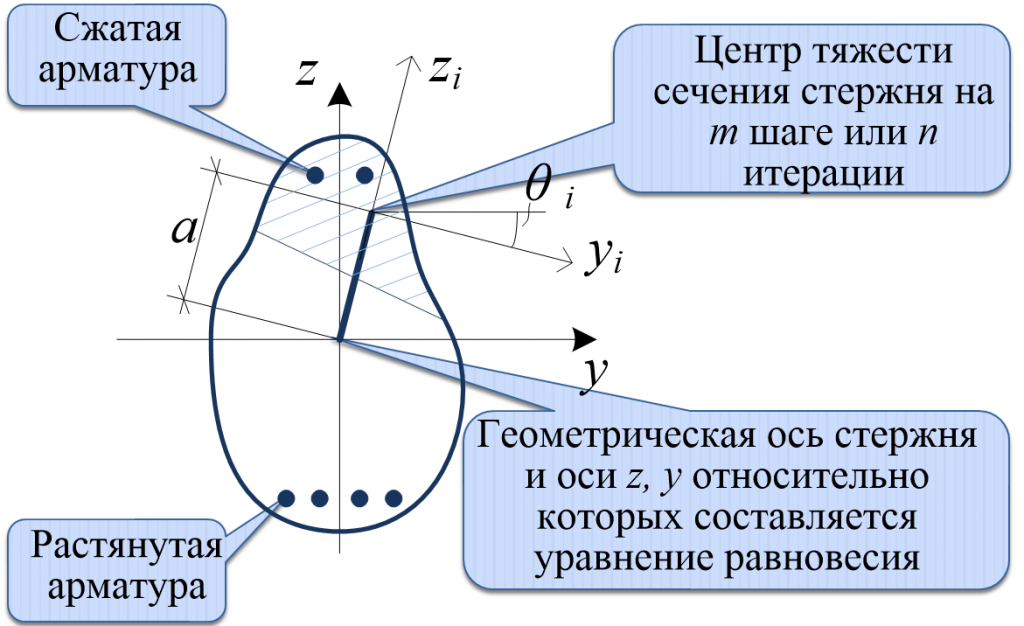
 Сложность задачи усугубляется еще и тем, что центр тяжести жесткостных характеристик смещается относительно геометрической оси стержня, относительно которой составляются и решаются уравнения равновесия (рис. 7).

Поэтому каждое i сечение имеет не только присущие ему на m шаге или на n итерации жесткостные характеристики (EI_yi, EI_zi, GI_кpi, EF_is, GI_кpi), но и абсолютно жесткую вставку a_i  и угол чистого вращения θ_i.

Что бы учесть эти эффекты необходимо по длине стержня вводить промежуточные узлы, что резко увеличивает размерность решаемой задачи. В этом случае целесообразно применить МСЭ аналогично описанной выше процедуре для стержня с переменным сечением по длине.

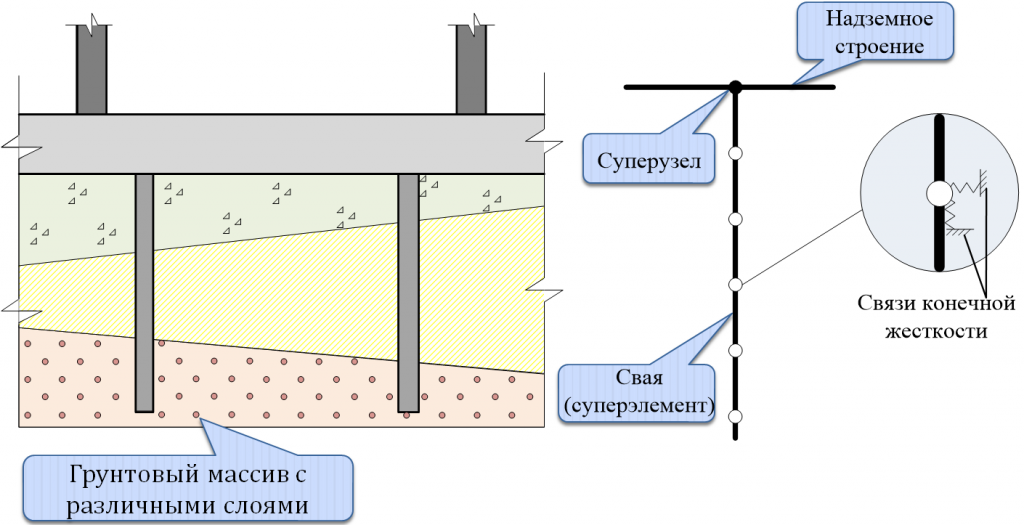
Применение МСЭ для построения матрицы жесткости сваи в грунтовом массиве

Взаимодействие сваи с грунтовым массивом (рис.8) может быть смоделировано введением по длине сваи дополнительных узлов и введение в эти узлы связей конечной жесткости по трем направлениям. Такой подход обуславливает резкое увеличение размерности задачи так как необходимо в расчетную схему включить надземное строение, фундаментную конструкцию, грунтовый массив и стержни (сваи) с большим количеством промежуточных узлов.

В этом случае целесообразно применение МСЭ. Стержень (свая) имеет один супер узел примыкания сваи к надземному строению. Построение матрицы жесткости аналогичной суперэлементной процедуре  для стержня переменной жесткости с той лишь разницей, что в промежуточных узлах кроме жесткостных характеристик собственно стержня учитываются жесткостные характеристики примыкающих связей конечной жесткости, учитывающее взаимодействие с соответствующим слоем грунта.

В этом случае при решении задачи взаимодействия надземного строения с грунтовым массивом моделируется введение связей только в суперузлах и отпадает необходимость включения в расчетную схему грунтового массива.

Реализация МСЭ представляется достаточно сложной, на территории бывшего СССР МСЭ был реализован в программном комплексе КАСКАД [10] программном комплексе МИРАЖ [11] и всех последующих программных комплексах семейства ЛИРА, включая современные версии ЛИРА-САПР.

Литература

1. Пржеминицкий Е. С. Матричный метод исследования конструкций на основе анализа подструктур. – Ракетная техника и космонавтика, 1963, №1.
   
2. Мейснер К. Алгоритм многосвязного объединения для метода жесткостей структурного анализа. – Ракетная техника и космонавтика, 1968, № 11.
   
3. Городецкий А. С. Численная реализация метода конечных элементов. – В кн.: Сопротивление материалов и теория сооружений. – Киев: Будивельник, 1973, вып. XX.
   
4. Городецкий А. С. Вычислительный комплекс для расчета строительных конструкций на ЭВМ «МИНСК-32». – В кн.: Организация, методы и технология проектирования, 1976, вып. 9.
   
5. Nagy L. I. Static Analysis Via Substructuring of an Experimental Vehicle Front – End Body Structure: Intern. Conf. on Vehicle Structural Mechanics: Finite Element Application to Vehicle Design – Detroit, Michigan,1974 ( March).
   
6. Neke I., Nagai K., Fuke H. General Purpose Program of Plane Stress Analysis by Finite Element Method and its Application. – IHI Engineering Rev., 1972, vol. 5, No.1.
   
7. Araldesen P. O., Roren E. M. Q. The finite Element Method using Superelements. The SESAM – 69 Struct. – In: Conf. on Modern Techniques of Ship Struct. Analysis and Design. – Berkley: University of California, 1970 (September).
   
8. Метод суперэлементов в расчете прочности судовых конструкций/ В. А. Постнов, С. А. Дмитриев, Б. К. Елтышев, А. А. Родионов. – Судостроение, 1975, №11.
   
9. Постнов В. А. , Родионов А. А., Ценков М. Ц. Метод суперэлементов в линейных и нелинейных задачах. – В кн.: Метод конечных элементов в строительной механике. – Горький: Изд-во ГГУ, 1975.
   
10. Постнов В. А., Дмитриев С. А., Елтышев Б. К., Родионов А. А. Метод суперэлементов в расчетах инженерных сооружений. – Л.: Судостроение, 1979.
    
11. Городецкий А. С. Программа «Мираж» для статического расчета конструкций методом конечных элементов, Сборник трудов Всесоюзной конференции «Автоматизация проектирования, как комплексная проблема совершенствования проектного дела в стране». – М.: 1973.
    
12. Городецкий А. С. Возможности применения суперэлементов при решении различных задач строительной механики/ Александр Сергеевич. Городецкий // Строительная механика и расчет сооружений. – 2015 – № 4. – С. 51-56
    

• суперэлемент
• матрица жесткости
• свая
• платформенный стык
• нелинейность