Демпфирование по Релею в ПК ЛИРА-САПР

Уравнение движения системы можно представить в виде:

(1)

где [C] – матрица демпфирования, [M] – матрица массы, [K] – матрица жёсткости, {Pt} – вектор узловых нагрузок, как функция от времени,{} – вектор узловых ускорений, {} – вектор узловых скоростей, {u} – вектор узловых перемещений.

Демпфирование по Рэлею известно, как пропорциональное демпфирование, которое выражается через линейную комбинацию матриц массы и жесткости.

(2),

где - коэффициент пропорциональности массы (с^-1), - коэффициент пропорциональности жёсткости (с).

С помощью ортогонального преобразования уравнение (1) сводится к виду

(3)

Уравнение (3) сводится к уравнению

(4),

где {} – перемещения в преобразованных координатах; – коэффициент демпфирования; – собственная частота; P(t) – вектор узловых нагрузок в преобразованных координатах.

Матрица демпфирования в таком случае представим в виде

  (5)

Перепишем (5)

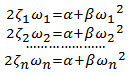(6)

Если система имеет 2 степени свободы, уравнение (6) сводится к

(7)

Для нахождения коэффициентов и необходимо решить уравнение (7).

Однако, решая системы с большим количеством степеней свободы (больше двух), проблематично определить такие коэффициенты, которые будут удовлетворять всем n-уравнениям. Но нам это и ненужно.

Как показано в уравнении (5), ортогональное преобразование матрицы демпфирования сводит матрицу [C] к форме

(8)

Разделим (8) на 2 и получим

(9)

Из уравнения (9) видно, что коэффициент демпфирования пропорционален частоте системы. График функции (9) имеет вид как на рисунке 1. Обратим внимание, что для первых (низших) частот график функции не линеен, а для более высоких – линеен.

Из рис. 1 видно, что для некоторого y = a/x + bx, когда x – небольшой, первое выражение a/x - преобладающее на начальном этапе и по мере возрастанияx -уменьшается и приближается к нулю, а выражение bx – возрастает. Другими словами, если система очень гибкая (гибкие антенны, очень длинные сваи, высокие трубы) и имеет небольшие низшие частоты, то она будет показывать нелинейные свойства демпфирования и будет меняться к линейным по мере возрастания собственных частот.

Однако, большинство конструкций обычно проектируются так, чтобы иметь достаточную жесткость, и, соответственно, имеют значительно более высокие низшие частоты, а выражение /2 будет доминирующим. Более того, принимая тот факт, что нелинейный фактор будет слишком мал для стандартных конструкций не будет ошибочным предположить, что коэффициент демпфирования каждой моды линейно зависим от частоты системы.

Для системы, которая имеет большое количество степеней свободы, только первые несколько частот соответствуют значительному динамическому влиянию.

Решим тестовый пример колебания двух рам. Геометрические и физические характеристики идентичны. К обеим рамам приложена одинаковая динамическая нагрузка.

В ПК ЛИРА-САПР реализована возможность учета демпфирования по Рэлею через коэффициенты и . Зная частоты собственных колебаний, а так же допустив, что решим уравнение (7).

(10),

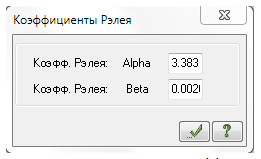
Откуда, узнаем = 3.383 и = 0.00206. И зададим их как на рисунке 2.

Рис. 3. Мозаика коэффициентов .

Рис. 4. Мозаика коэффициентов .

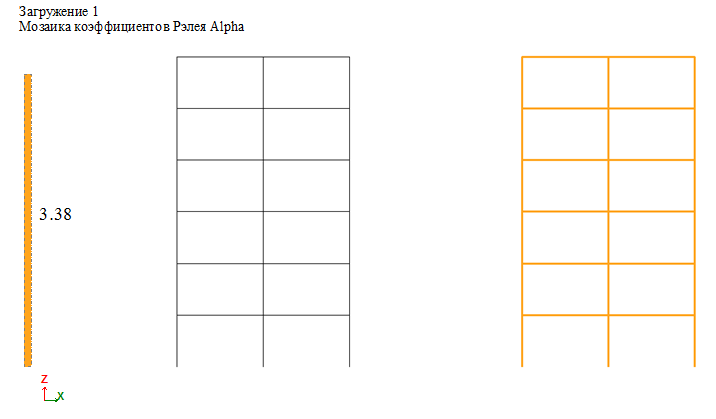
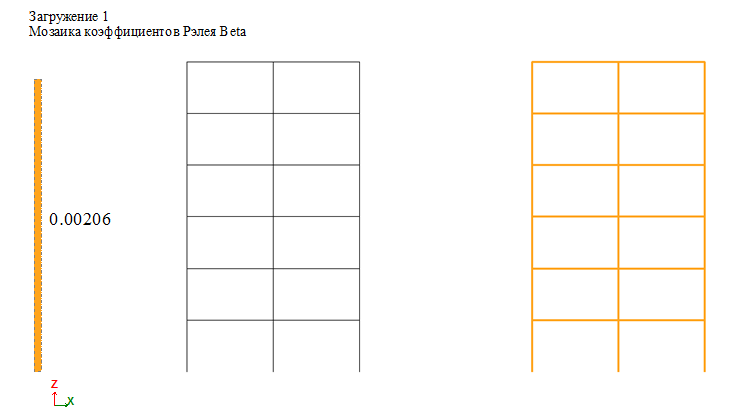
Рассмотрим результаты расчета (перемещения вдоль оси X) указанных на рис. 5 точек 104 и 336.

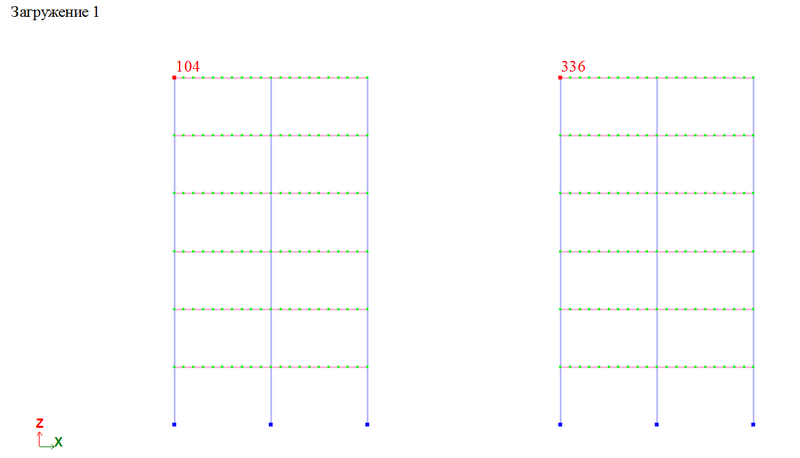
Если сравнить результаты расчета, то мы увидим, что во время движения первой схемы (левой на рис. 5) энергия в ней совершенно не рассеивается, и колебания никогда не прекратятся, чего не может быть на практике. Для того, чтобы учитывать затухание во всей конструкции, в ПК ЛИРА-САПР реализовано демпфирование по Рэлею. В котором матрица демпфирования заполняется через коэффициенты пропорциональности матрицам массы и жесткости.

• динамическое воздействие
• демпфирование
• коэффициент Рэлея
• колебание
• частота