Ольга Башинская

Учёт совместной работы поперечных и продольных стен при действии горизонтальной нагрузки

Изменено 10.02.2023 | Создано 20.07.2022

В ЛИРА-САПР 2022 реализована проверка кирпичных простенков на действие горизонтальной нагрузки с учётом совместной работы поперечных и продольных стен, в соответствии с нормами СНиП II-22-81 “Каменные и армокаменные конструкции”. В основе данного расчёте заложен алгоритм, который автоматически опредеяет форму простенка, а также анализирует расположение продольных и поперечных элементов стены.

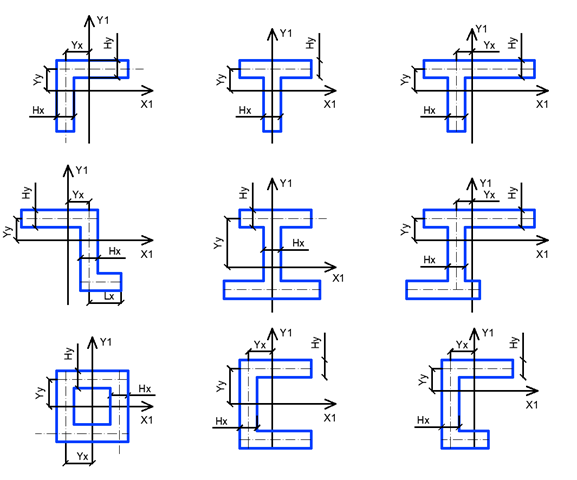
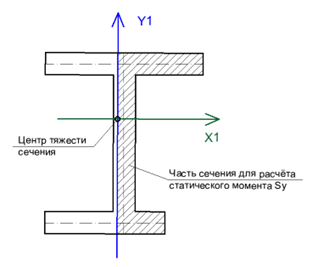
В данном расчёте распознаются следующие формы простенков: прямоугольник, уголок, тавр, двутавр, крест, швеллер, сечение типа Z, короб. Каждое из рассматриваемых сечений имеет свою собственную систему координат с осями X1,Y1, которая может не совпадать с общей системой координат расчётной модели XоY. Внешние нагрузки прикладываются к расчётной схеме в глобальной системе координат, поэтому в данном расчёте рассматриваются проекции действующих усилий на локальные оси простенка X1,Y1 (рис. 1).


Рис. 1. Система координат простенка

Рис. 1. Система координат простенка.

1. Проверка на сдвигающее усилие в пределах одного этажа.

1.1. Проверка на сдвигающее усилие в пределах одного этажа осуществляется по формуле (СНиП II-22-81, пункт 6.11, формула 38):

ф-ла 1.png

(1)

где T – сдвигающее усилие в пределах одного этажа;

Q – проекция расчетной поперечной силы от горизонтальной нагрузки на локальные оси простенка;

A – в случае проверки на усилие Qy1, A – это площадь сечения полки; в случае проверки на усилие Qx1, A – это площадь сечения стенки;

y – расстояние от оси продольной стены до оси, проходящей через центр тяжести сечения стен в плане (далее по тексту обозначается как Yx, Yy), подробное описание этого параметра в разделе 1.2;

H – высота этажа;

I – момент инерции сечения стен относительно оси, проходящей через центр тяжести сечения;

h – толщина поперечной стены (далее по тексту обозначается как Hx, Hy), подробное описание этого параметра в разделе 1.2;

Rsq – расчетное сопротивление кладки срезу по вертикальному перевязанному сечению.

В случае воздействия усилия Qx1, проверка принимает вид:

ф-ла 2.png

(2)

В случае воздействия усилия Qy1, проверка принимает вид:

ф-ла 3.png

(3)

1.2. Определение геометрических параметров у (Yx, Yy) и h (Hx, Hy), что зависят от формы простенка.

Такие параметры как расстояние от оси продольной (или поперечной) стены до оси, проходящей через центр тяжести сечения (Yx, Yy) и толщина поперечной стены (или полки) (Hx, Hy) зависят от формы простенка, поэтому на рисунке 2 показано их расположение для каждого типа простенка отдельно.


Рис. 2. Определение y и h для каждого типа простенка

Рис. 2. Определение y и h для каждого типа простенка.

Замечание 1: для сечений, у которых ось продольной или поперечной стены совпадает с центром тяжести простенка, – параметры Yx = Yy = 0. Поэтому некоторые симметричные сечения автоматически не проходят данную проверку. К примеру, простенок типа «прямоугольник» сразу относится к простенкам, которые не проходят данную проверку. Также, некоторые симметричные сечения (тавр, двутавр, крест, сечение типа Z) будут попадать в список сечений, которые не проходят проверку в том случае, если к ним приложено усилие, что действует перпендикулярно оси симметрии.

2. Проверка на главные растягивающие напряжения.

2.1. Проверка на главные растягивающие напряжения осуществляется по формуле (СНиП II-22-81, пункт 6.12, формула 39):

ф-ла 4.png

(4)

где Q – проекция расчетной поперечной силы от горизонтальной нагрузки на локальные оси простенка;

Rtq – расчетное сопротивление скалыванию кладки;

h – толщина поперечной (или продольной) стены (далее по тексту обозначается как Hx, Hy), подробное описание этого параметра в разделе 2.3;

L – длина поперечной (или продольной) стены в плане, если в сечение входят полки в виде отрезков наружных стен, то L – это расстояние между осями этих полок (далее по тексту обозначается как Lx, Ly), подробное описание этого параметра в разделе 2.3;

ν – коэффициент неравномерности касательных напряжений в сечении, подробное описание этого параметра в разделе 2.2.

Расчетное сопротивление скалыванию кладки Rtq определяется по формуле (СНиП II-22-81, пункт 6.12, формула 41):

ф-ла 5.png

(5)

где Rtw – расчетное сопротивление главным растягивающим напряжениям.

Напряжение σ0 определяется по формуле (СНиП II-22-81, пункт 6.12, формула 42):

ф-ла 6.png

(6)

где N – усилие сжатия; А – площадь сечения всего простенка.

В случае воздействия усилия Qx1, формула (4) принимает вид:

ф-ла 7.png

(7)

В случае воздействия усилия Qy1, формула (4) принимает вид:

ф-ла 8.png

(8)

2.2. Определение коэффициента неравномерности касательных напряжений ν.

В некоторых случаях коэффициент ν принимается стандартным, а именно при расчёте на усилие Qy1, для следующих типов сечений:

  • для двутавровых сечений ν = 1,15;
  • для тавровых сечений ν = 1,35;
  • для прямоугольных сечений (без учета работы продольных стен) ν = 1,5.

Во всех остальных случаях, коэффициент неравномерности касательных напряжений ν определяется по формуле:

ф-ла 9.png

(9)

где S0 – статический момент части сечения, находящейся по одну сторону от оси, проходящей через центр тяжести сечения;

I – момент инерции всего сечения.

Поскольку статический момент части сечения S0 будет отличаться в зависимости от оси (X1 или Y1), относительно которой рассматривается несущая способность простенка, следовательно, коэффициент неравномерности касательных напряжений ν также будет отличаться в зависимости от направления, которое рассматривается. Поэтому в расчёте отдельно принимают участие νX и νY.

2.3. Определение геометрических параметров h (Hx, Hy) и L (Lx, Ly), что зависят от формы простенка.

Такие параметры как h – толщина поперечной (или продольной) стены (Hx, Hy) или L – длина поперечной (или продольной) стены (Lx, Ly) зависят от формы простенка, поэтому на рисунке 3 показано их расположение для каждого типа простенка отдельно.


Рис. 3. Определение L и h для каждого типа простенка

Рис. 3. Определение L и h для каждого типа простенка.

3. Особенности расчёта прямоугольных или симметричных простенков.

В этой статье, раздел 1.1, замечание 1, сказано, что некоторые простенки автоматически не проходят проверку по формуле 1 (проверка на сдвигающее усилие в пределах одного этажа), но при этом они могут проходить проверку на главные растягивающие напряжения. Примером такого простенка может быть прямоугольный простенок, или симметричный тавр, в котором действует напряжение в направлении Qx1.

Поэтому, при просмотре изополей по коэффициенту запаса, такие сечения сразу попадают в диапазон «ошибок» (Рис. 4). Это сделано для того, чтобы обратить внимание пользователя на то, что есть простенки, которые плохо воспринимают воздействие поперечной нагрузки, и для лучшей совместной работы поперечных и продольных стен возможно стоит поменять расположение простенков.


Рис. 4. Пример сечения, которое автоматически попадает в диапазон «ошибки»

Рис. 4. Пример сечения, которое автоматически попадает в диапазон «ошибки».

Но для таких простенков можно увидеть результаты расчёта на главные растягивающие напряжения (формула 4). Для этого нужно воспользоваться файлом отчёта .тхт, в котором расписаны все проверки.

О том, как пользоваться файлом отчёта для кирпичных простенков, подробно расписано в статье (раздел «7. Файл отчёта»):

4. Пример расчёта.

4.1. Исходные данные.

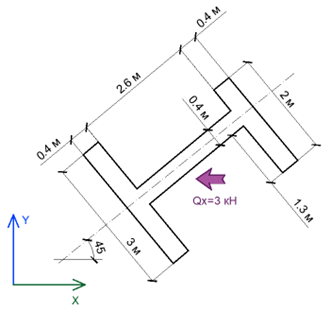
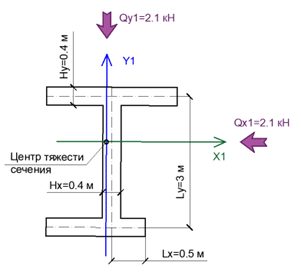
Необходимо выполнить анализ совместной работы поперечных и продольных стен простенка, что показан на рисунке 5. Действующие усилия: N = 30 кН, Qx = 3 кН. Характеристики кладки: Rtw = 0.25 МПа, Rsq = 0.24 МПа. Высота этажа Н = 3 метра. Площадь сечения простенка А = 3.04 м2. Моменты инерции сечения относительно локальных осей X1 и Y1: IX = 4.99 м4, IY = 1.33 м4.


Рис. 5. Схема к расчёту стены при действии горизонтальных нагрузок

Рис. 5. Схема к расчёту стены при действии горизонтальных нагрузок.

4.2. Пример расчёта на сдвигающее усилие в пределах одного этажа.

Определим проекции усилия Qx на локальные оси простенка X1 и Y1:

ф-ла 10.png

(10)

ф-ла 11.png

(11)

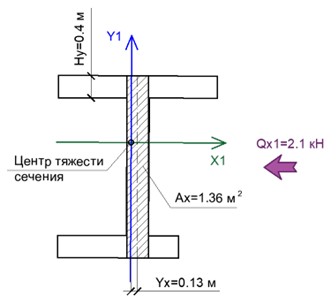
По формуле (2) выполним проверку на сдвигающее усилие QX1. Геометрические параметры, что используются при данном проверке показаны на рисунке 6.

ф-ла 12.png

(12)

ф-ла 13.png

(13)

ф-ла 14.png

(14)


Рис. 6. Схема к расчёту простенка на сдвигающее усилие Q_X1

Рис. 6. Схема к расчёту простенка на сдвигающее усилие QX1.

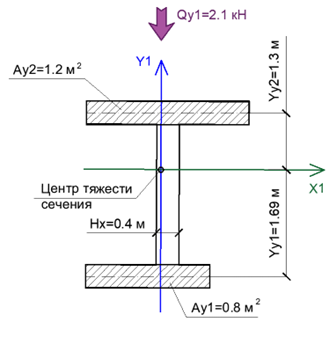
По формуле (3) выполним проверку на сдвигающее усилие QY1. Параметры AY и YY выбираются в зависимости от меньшего произведения между (Ay1∙Yy1) и (Ay2∙Yy2) (Рис. 7). Геометрические параметры, что используются в данной проверке показаны на рисунке 6.

Поскольку (Ay1 ∙ Yy1 = 0.8 ∙ 1.69 = 1.352) < (Ay2 ∙ Yy2 = 1.2 ∙ 1.3 = 1.56), поэтому AY = Ay1 = 0.8; YY = Yy1 = 1.69.

ф-ла 15.png

(15)

ф-ла 16.png

(16)

ф-ла 17.png

(17)


Рис. 7. Схема к расчёту простенка на сдвигающее усилие Q_Y1

Рис. 7. Схема к расчёту простенка на сдвигающее усилие QY1.

Замечание: Подробную трассировку расчёта можно увидеть в файле отчёта .тхт, о котором можно прочитать тут. Пример отчёта для рассматриваемой задачи выглядит следующим образом:

Проверка на вертикальные и горизонтальные нагрузки:


Рис. 8. Пример файла отчёта после расчёта простенка

Рис. 8. Пример файла отчёта после расчёта простенка.

4.3. Пример расчёта на главные растягивающие напряжения.

По формулам (7) и (8) выполним проверку на сдвигающие усилия QX1 и QY1. Геометрические параметры, что используются при данном расчёте показаны на рисунке 8.

ф-ла 18.png

(18)

ф-ла 19.png

(19)

1) Pассмотрим воздействие усилия QX1 = 2.1 кН:

Статический момент части сечения, находящейся по одну сторону от оси Y1 (Рис. 9):

SY = 0.755 м3.


Рис. 9. Схема для расчёта статического момента части сечения S_(Y )

Рис. 9. Схема для расчёта статического момента части сечения SY.

По формуле (5) определим коэффициент неравномерности касательных напряжений ν:

ф-ла 20.png поэтому принимаем νX = 1.

(20)

ф-ла 21.png

(21)

ф-ла 22.png

(22)

2) Pассмотрим воздействие усилия QX1 = 2.1 кН:

Согласно разделу 2.2, для двутаврового сечения коэффициент неравномерности касательных напряжений ν = 1.15.

ф-ла 23.png

(23)

ф-ла 24.png

(24)


Рис. 10. Схема к расчёту простенка на главные растягивающие напряжения

Рис. 10. Схема к расчёту простенка на главные растягивающие напряжения.

Замечание: Подробную трассировку расчёта можно увидеть в файле отчёта .тхт, о котором можно прочитать тут. Пример отчёта для рассматриваемой задачи выглядит следующим образом:


Рис. 11. Пример файла отчёта после расчёта простенка

Рис. 11. Пример файла отчёта после расчёта простенка.

4.4. Задание исходных данных в ЛИРА-САПР.

Поскольку в данном расчёте не происходит подбор армирования или проверка на сжатие, рекомендуется выполнять данный расчёт в отдельном варианте конструирования, который будет предназначен только для анализа работы конструкции на горизонтальную нагрузку.

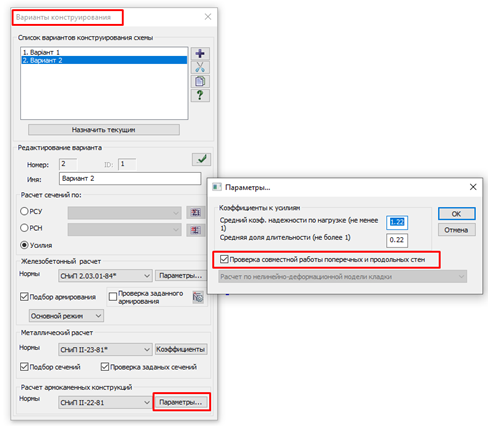
Для того, чтобы выполнить анализ совместной работы поперечных и продольных стен, необходимо открыть диалоговое окно «Варианты конструирования». В разделе «Расчёт армокаменных конструкций» нужно нажать на кнопку «Параметры». В открывшемся диалоге «Параметры» нужно поставить галочку «Проверка совместной работы поперечных и продольных стен» (Рис. 12).


Рис. 12. Формирование варианта конструирования

Рис. 12. Формирование варианта конструирования.

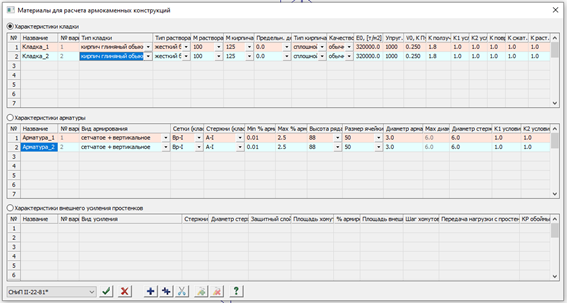
Характеристики материалов задаются в диалоговом окне «Материалы для расчёта армокаменных конструкций», рис. 13.


Рис. 13. Формирование варианта конструирования

Рис. 13. Формирование варианта конструирования.

Мозаику коэффициентов запаса при анализе совместной работы продольных и поперечных стен показано на рисунке 14.


Рис. 14. Мозаика коэффициентов запаса

Рис. 14. Мозаика коэффициентов запаса.

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

  • 1.6K
Поделиться публикацией:

Ольга Башинская

Кандидат технических наук - специальность "Строительные конструкции, здания и сооружения". Инженер-программист компании «ЛИРА САПР». Разработка программных комплексов.

Другие публикации этого автора

Комментарии

Написать

Другие материалы