В ПК ЛИРА-САПР версии 2020 реализован расчет каменных и армокаменных конструкций по следующим нормам:
- СНиП ІІ-22-81*;
- СП 15.13330.2012;
- ДБН В.2.6-162:2010.
Расчёт производится по предельным состояниям первой и второй группы.
На первом этапе расчета, все простенки проходят проверку по формулам для расчёта каменных конструкций. Если простенок не проходит проверку по расчету каменных конструкций, тогда выполняется подбор арматуры и совершается проверка соответствующего простенка по формулам для расчета армокаменных конструкций.
Данный расчёт является универсальным для простенков любой формы, поэтому в расчёте не используются упрощенные методы, предложенные для прямоугольных сечений. К примеру, гибкость в данном расчете, всегда зависит от радиуса инерции сечения, а не от высоты сечения. А также, для более точного расчета промежуточных коэффициентов, которые при упрощенных методах расчёта прямоугольных сечений могут зависеть от высоты сечения, мы всегда принимаем эти коэффициенты зависимыми от расстояния от центра тяжести сечения элемента до его края в сторону эксцентриситета. Конкретные примеры указаны в формулах 2, 7, 12, 23.
1. Случай продольных усилий сжатия (СП 15.13330.2012 и СНиП ІІ-22-81*)
1.1. Расчет каменных конструкций
Расчёт производится по формуле:
 , (1)
, (1)
где  – коэффициент, определяемый по формуле:
– коэффициент, определяемый по формуле:
 , (2)
, (2)
где  - расстояния от центра тяжести сечения элемента до его края в сторону эксцентриситета;
- расстояния от центра тяжести сечения элемента до его края в сторону эксцентриситета;
 - коэффициент продольного изгиба, который определяется по формуле:
- коэффициент продольного изгиба, который определяется по формуле:
 , (3)
, (3)
где 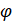 - коэффициент продольного изгиба для всего сечения, который зависит от гибкости простенка
- коэффициент продольного изгиба для всего сечения, который зависит от гибкости простенка  , которая всегда определяется по формуле:
, которая всегда определяется по формуле:
 , (4)
, (4)
где  – расчетная длина (высота) элемента,
– расчетная длина (высота) элемента,  – минимальный радиус инерции сечения.
– минимальный радиус инерции сечения.
 - коэффициент продольного изгиба для сжатой части сечения, который зависит от гибкости простенка
- коэффициент продольного изгиба для сжатой части сечения, который зависит от гибкости простенка  , которая всегда определяется по формуле:
, которая всегда определяется по формуле:
 , (5)
, (5)
где  – радиус инерции сжатой части сечения, который определяется по деформационной модели (смотри раздел 3).
– радиус инерции сжатой части сечения, который определяется по деформационной модели (смотри раздел 3).
В случае центрального сжатия коэффициент продольного изгиба  принимается равным:
принимается равным:
 . (6)
. (6)
 – расчетное сопротивление сжатию кладки;
– расчетное сопротивление сжатию кладки;
 – площадь сжатой зоны, в случае центрального сжатия равна площади всего сечения. При наличии эксцентриситета площадь сжатой зоны определяется по деформационной модели (смотри раздел 3).
– площадь сжатой зоны, в случае центрального сжатия равна площади всего сечения. При наличии эксцентриситета площадь сжатой зоны определяется по деформационной модели (смотри раздел 3).
 – коэффициент, который определяется по формуле:
– коэффициент, который определяется по формуле:
 , (7)
, (7)
1.2. Расчет армокаменных конструкций
Расчёт производится по формуле:
 , (8)
, (8)
Значения  ,
,  ,
,  ,
,  описаны выше.
описаны выше.
 – расчётное сопротивление армированной кладки, которое определяется по формуле:
– расчётное сопротивление армированной кладки, которое определяется по формуле:
 , (9)
, (9)
 – коэффициент, что зависит от пустотности кирпича;
– коэффициент, что зависит от пустотности кирпича;
 – расчетное сопротивление арматуры;
– расчетное сопротивление арматуры;
 – процент армирования, что рассчитывает по формуле:
– процент армирования, что рассчитывает по формуле:
 , (10)
, (10)
 – площадь сечения арматуры;
– площадь сечения арматуры;
 – размер ячейки;
– размер ячейки;
 – расстояние между осями поперечных связей при стальных обоймах или между хомутами при железобетонных и штукатурных обоймах.
– расстояние между осями поперечных связей при стальных обоймах или между хомутами при железобетонных и штукатурных обоймах.
Случай продольных усилий сжатия (ДБН В.2.6-162:2010)
1.1. Расчет каменных конструкций
Расчёт производится по формуле:
 , (11)
, (11)
где  – коэффициент понижения несущей способности простенка, что определяется по формуле:
– коэффициент понижения несущей способности простенка, что определяется по формуле:
 , (12)
, (12)
где  - расстояния от центра тяжести сечения элемента до его края в сторону эксцентриситета;
- расстояния от центра тяжести сечения элемента до его края в сторону эксцентриситета;
 – площадь сжатой зоны, в случае центрального сжатия равна площади всего сечения. При наличии эксцентриситета площадь сжатой зоны определяется по деформационной модели (смотри раздел 4);
– площадь сжатой зоны, в случае центрального сжатия равна площади всего сечения. При наличии эксцентриситета площадь сжатой зоны определяется по деформационной модели (смотри раздел 4);
 – расчетное сопротивление сжатию кладки.
– расчетное сопротивление сжатию кладки.
1.2. Расчет армокаменных конструкций
Расчёт производится по формуле:
 , (13)
, (13)
Значения  описаны выше.
описаны выше.
 – расчётное сопротивление армированной кладки, которое определяется по формуле:
– расчётное сопротивление армированной кладки, которое определяется по формуле:
 , (14)
, (14)
 , (15)
, (15)
2. Случаи изгибающего момента, поперечной силы или растяжения
Поскольку моменты могут быть приложены только в плоскостях, что перпендикулярны горизонтальным швам, расчёт на изгибающий момент производится по НЕперевязанному сечению, и расчетное сопротивление кладки зависит от марки раствора (рисунок 1, а).
Поскольку поперечная сила может быть приложена в плоскостях, что параллельны горизонтальным швам, расчет на поперечную силу производится по Перевязанному сечению, и расчетное сопротивление кладки зависит от марки раствора (рисунок 1, б).
Поскольку растягивающее усилие может быть приложено только в плоскости, что перпендикулярна горизонтальным швам, расчет на растягивающую продольную силу производится по НЕперевязанному сечению, и расчетное сопротивление кладки зависит от марки раствора (рисунок 1, в).

3. Подбор параметров для расчёта по деформационной модели
Площадь сжатой зоны определяется по деформационной теории, что позволяет учесть нелинейную работу кирпичной кладки в сечении. При этом, используется кусочно-линейная зависимость между напряжениями и деформациями кладки (рис. 2).
Параметры для формирования закона деформации материала определяются в соответствии с разделом 6 норм СП 15.13330.2012:
|
Модуль упругости (начальный модуль деформации) определяется по формуле:
где
В диалоговом окне «Характеристиках кладки» есть возможность задать предельные деформации кладки. Если предельные деформации не были заданы пользователем (то есть равны нулю), тогда они определяются по следующему алгоритму. Рассмотрим формулу для нахождения деформаций кладки:
|

Рисунок 2. Кусочно-линейная зависимость между напряжениями и деформациями
|
Для того, чтобы найти предельные деформаций кладки  , в формулу (17), вместо напряжений
, в формулу (17), вместо напряжений  подставим значение временного сопротивления сжатию кладки, и получим формулу для определения предельных деформаций кладки
подставим значение временного сопротивления сжатию кладки, и получим формулу для определения предельных деформаций кладки  :
: 
 (18)
(18)
Таким образом, предельные деформации кладки принимаются обратно пропорциональными от упругой характеристики  , которую задаёт пользователь.
, которую задаёт пользователь.
Поскольку формула (17) отображает нелинейную зависимость между деформациями и напряжениями, мы запишем её в вывернутом виде и получим формулу для нахождения предельных напряжений  :
:
 (19)
(19)
4. Расчет по предельным состояниям второй группы
Данный расчёт производится для любых норм в том случае, если в диалоговом окне «Материалы для расчёта армокаменных конструкций» коэффициент условий работы К2 не равен нулю, а также при наличии продольных усилий в простенке. Чтобы не производить расчет по предельным состояниям второй группы, необходимо задать коэффициент К2 равным нулю (рисунок 3).

Расчёт по предельным состояниям второй группы производится по формуле:
 , (20)
, (20)
 – коэффициент условий работы кладки, что задается пользователем (рисунок 3);
– коэффициент условий работы кладки, что задается пользователем (рисунок 3);
 – расчетное сопротивление кладки при изгибе;
– расчетное сопротивление кладки при изгибе;
 момент инерции сечения.
момент инерции сечения.
Результаты расчета по второму предельному состоянию можно увидеть в файле отчета .txt (смотри раздел 7).
5. Усиление каменных конструкций
В ПК «ЛИРА-САПР» реализована возможность расчета усиления существующего простенка тремя методами:
- стальной обоймой (рис.4, а);
- железобетонной обоймой (рис. 4, б);
- армированной растворной обоймой (рис. 4, в).

Расчет усиления производится в соответствии с Пособием по проектированию каменных и армокаменных конструкций, а именно пунктами 5.34 – 5.39.
1. Расчет усиления стальной обоймой производится по формуле:
 ; (21)
; (21)
2. Расчет усиления железобетонной обоймой производится по формуле:
 ; (22)
; (22)
3. Расчет усиления армированной растворной обоймой производится по формуле
 . (23)
. (23)
Где  ,
,  – коэффициенты, которые в случае центрального сжатия принимаются равными 1, а при наличии эксцентриситета вычисляются по формулам:
– коэффициенты, которые в случае центрального сжатия принимаются равными 1, а при наличии эксцентриситета вычисляются по формулам:
 ;
;  ; (24)
; (24)
 – коэффициент, что описан выше (формула 3);
– коэффициент, что описан выше (формула 3);
 – коэффициент условий работы кладки, который задаётся в поле «Характеристики кладки» диалогового окна «Материалы для расчета армокаменных конструкций» (рисунок 5);
– коэффициент условий работы кладки, который задаётся в поле «Характеристики кладки» диалогового окна «Материалы для расчета армокаменных конструкций» (рисунок 5);
 – коэффициент, учитывающий влияние длительного воздействия нагрузки (формула 2);
– коэффициент, учитывающий влияние длительного воздействия нагрузки (формула 2);
 – расчетное сопротивление кладки;
– расчетное сопротивление кладки;
 – процент армирования хомутами, что определяется по формуле:
– процент армирования хомутами, что определяется по формуле:
 ; (25)
; (25)
 - площадь сечения хомутов при железобетонных и штукатурных обоймах или поперечных планок при стальных обоймах (рисунок 4);
- площадь сечения хомутов при железобетонных и штукатурных обоймах или поперечных планок при стальных обоймах (рисунок 4);
 ,
,  – размеры сторон усиливаемого элемента;
– размеры сторон усиливаемого элемента;
 – расстояние между осями поперечных связей при стальных обоймах или между хомутами при железобетонных и штукатурных обоймах;
– расстояние между осями поперечных связей при стальных обоймах или между хомутами при железобетонных и штукатурных обоймах;
 – расчетное сопротивление поперечной арматуры обоймы;
– расчетное сопротивление поперечной арматуры обоймы;
 – площадь сечения усиливаемой кладки;
– площадь сечения усиливаемой кладки;
 – расчетное сопротивление уголков или продольной сжатой арматуры;
– расчетное сопротивление уголков или продольной сжатой арматуры;
 - площадь сечения продольных уголков стальной обоймы или продольной арматуры железобетонной обоймы (рисунок 4);
- площадь сечения продольных уголков стальной обоймы или продольной арматуры железобетонной обоймы (рисунок 4);
 – коэффициент условий работы бетона;
– коэффициент условий работы бетона;
 – расчётное сопротивление бетона обоймы;
– расчётное сопротивление бетона обоймы;
 – площадь сечения бетона обоймы, заключенная между хомутами и кладкой (без учёта защитного слоя);
– площадь сечения бетона обоймы, заключенная между хомутами и кладкой (без учёта защитного слоя);

Расчетные сопротивления арматуры, применяемой при устройстве обоймы, принимаются в соответствии с таблицей 10 из Пособия по проектированию каменных и армокаменных конструкций:
|
Армирование |
Расчетные сопротивления арматуры, МПа |
|
|
Сталь класса А-І |
Сталь класса А-ІІ |
|
|
Поперечная арматура |
150 |
190 |
|
Продольная арматура без непосредственной передачи нагрузки на обойму |
43 |
55 |
|
То же, при передаче нагрузки на обойму с одной стороны |
130 |
160 |
|
То же, при передаче нагрузки на обойму с двух сторон |
190 |
240 |
5.1. Усиление стальной обоймой
Для задания расчета усиления стальной обоймой необходимо заполнить следующие поля «Характеристик внешнего усиления» диалогового окна «Материалы для расчета армокаменных конструкций»:

В поле Стержни (класс арматуры) задается класс арматуры, который является одинаковым для вертикальных уголков и поперечной полосы (хомута).
В поле Площадь хомутов поперечного армирования задается площадь сечения одной планки поперечной полосы (хомута) As (рисунок 7).
В поле Площадь внешнего усиления задается суммарное значение площадей продольных уголков стальной обоймы As’ (рисунок 7).
В поле Шаг хомутов по высоте задается расстояние между осями поперечных связей s (рисунок 7).
В поле КР обоймы автоматически выбирается коэффициент условий работы бетона, который зависит от вида Передачи нагрузки с простенка на обойму.

5.2. Усиление железобетонной обоймой
Для задания расчета усиления железобетонной обоймой необходимо заполнить следующие поля «Характеристик внешнего усиления» диалогового окна «Материалы для расчета армокаменных конструкций»:

В поле Стержни (класс арматуры) задается класс арматуры, который является одинаковым для вертикальной и поперечной арматуры.
В поле Диаметр стержней задается диаметр поперечной арматуры (хомута) Аs (рисунок 9).
В поле Защитный слой вертик. арматуры задается толщина бетонного слоя обоймы, заключенная между хомутами и кладкой (без учета защитного слоя) b (рисунок 9).
В поле Площадь внешнего усиления задается суммарное значение площадей продольной арматуры обоймы As’ (рисунок 9).
В поле Шаг хомутов по высоте задается расстояние между хомутами s (рисунок 9).
В поле КР обоймы автоматически выбирается коэффициент условий работы бетона, который зависит от вида Передачи нагрузки с простенка на обойму.

5.3. Усиление армированной растворной обоймой
Для задания расчета усиления армированной растворной обоймой необходимо заполнить следующие поля «Характеристик внешнего усиления» диалогового окна «Материалы для расчета армокаменных конструкций»:

В поле Стержни (класс арматуры) задается класс арматуры, который является одинаковым для вертикальной и поперечной арматуры.
В поле Диаметр стержней задается диаметр поперечной арматуры (хомута) Аs (рисунок 9).
В поле Шаг хомутов по высоте задается расстояние между хомутами s (рисунок 9).
В поле КР обоймы автоматически выбирается коэффициент условий работы бетона, который зависит от вида Передачи нагрузки с простенка на обойму.
6. Результаты расчёта
После расчёта, на расчётной схеме будут отображены результаты расчета простенков только на центральное или внецентренное сжатие. Результаты расчёта простенков на изгибающий момент или на срез можно посмотреть в дополнительном текстовом файле отчёта.
7. Файл отчёта
После расчёта каменных конструкций, автоматически создаётся файл отчета в формате .txt, в котором для каждого простенка записаны все промежуточные расчётные значения.
Этот файл создаётся в папке Work, расположение которой можно найти следующим образом:
заходим в Меню приложения – Настройки – Каталоги – Файлы документации – Открыть каталог с помощью "Проводника", как показано на рисунках 11 и 12.


Как найти нужный простенок в текстовом файле?
|
При необходимости можно получить быстрый доступ к нужному простенку в файле. Для этого следует открыть текстовый файл, нажать
Рисунок 13. Нахождение нужного простенка
Узнать высоту отметки и номер группы интересующего Вас простенка можно в диалоговом окне «Характеристики группы простенков» (рис. 14). Для того чтобы открыть это окно, необходимо активировать функцию «фонарик» и указать интересующий Вас простенок. |
Рисунок 14. Характеристики простенков
|
8. Нелинейная деформационная модель.
Что это и зачем это нужно для кирпича?
Что такое нелинейная деформационная теория? Это метод расчёта несущей способности конструкции, который позволяет учесть нелинейную работу материала, а именно нелинейную зависимость между напряжениями и деформациями в материале. Это официально принятая (63.13330.2012 «Бетонные и железобетонные конструкции. Основные положения») методика расчета напряжений в элементе, с учётом физической нелинейности материала. Другими словами, если вы хотите учесть физическую нелинейность кирпича или железобетона, нелинейная деформационная теория – это допустимый способ это сделать.
Альтернативными методами расчёта конструкций есть расчёт по допускаемым напряжениям, разрушающим усилиям, предельным состояниям. При расчёте по предельным усилиям, элементы могут быть рассчитаны с учётом (рисунок 16) , или без учёта (рисунок 17) сопротивления бетона в растянутой зоне. В первом случае, усилия в изгибаемом элементе определяются по формуле:
|
Рисунок 15.
|
|
(26) (27) |
Выражение 27 представляет собой закон Гука при изгибе для стержня.

Исходя из таких допущений, мы можем рассчитывать несущую способность элемента по упрощенным формулам:
 ;
;
 ;
;
 ;
;
где  ,
,  ,
,  - соответствующие расчётные сопротивления,
- соответствующие расчётные сопротивления,  – площадь сечения,
– площадь сечения,  – момент сопротивления сечения,
– момент сопротивления сечения,  – дополнительные коэффициенты запаса.
– дополнительные коэффициенты запаса.
Но на самом деле, зависимость между напряжениями и деформациями может быть линейной только в случае малых напряжений. С увеличением нагрузки, эпюра напряжений в сечении становится все более нелинейной, как показано на рисунке 18.

Поэтому методы расчёта, основанные на методе предельных усилий или предельных состояний являются упрощенными. Чтобы правильно учитывать работу материалов, нужно учитывать нелинейную зависимость между напряжениями и деформациями. Для этого используется нелинейная деформационная модель.

При расчёте по деформационной модели, сечение разбивается на малые участки, далее итерационным методом происходит подбор (поиск) напряжений на каждом участке (как показано на рисунке 19), которые будут удовлетворять уравнение равновесия:

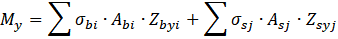

При этом, учитывается нелинейная зависимость между напряжениями и деформациями, которая выражается через выбранный график работы материала (рисунок 20).

В нормах СП 15.13330.2012 предложена упрощенная эпюра напряжений в сечении, когда простенок рассчитывается без учёта сопротивления кладки в растянутой зоне, как показано на рисунке 17.
Но согласно пункту 6.23, СП 15.13330.2012 для расчёта можно использовать нелинейную зависимость между напряжениями и деформациями. Поэтому, в ПК «ЛИРА-САПР» для определения площади сжатой зоны используется нелинейная деформационная теория, которая даёт возможность учесть нелинейную зависимости между деформациями и напряжениями в сечении.
А также, благодаря тому, что при таком подходе сечение разбивается на малые участки, происходит более точный расчёт простенков неправильной формы. К примеру, в СП сказано, что в упрощенных методах расчета разрешается пренебречь участками сечения, которые усложняют его форму. При использовании деформационной теории, все участки сечения принимают участие в работе элемента.
Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.


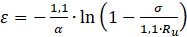








Комментарии 4