Objective
To determine the stress–strain state of a beam (on an elastic horizontal foundation) under the concentrated vertical forces.
Reference
M. Courtand et P. Lebelle, Formulaire du beton arme, t.2, Paris, Eyrolles,1976, p. 382.
Problem statement
To determine the vertical displacements Z at the mid-span (point C) and at the beam ends (points A and B), the rotation angles UY at the beam ends, as well as the bending moment M at the mid-span of the beam.
Design model
A beam resting on an elastic horizontal foundation with constant stiffness along its length. A beam is subjected to three concentrated vertical forces of equal value F, applied at the beam ends (points A and B) and at the mid-span (point C).
Geometry
Beam length l = 4,967294133 m
Width of settlement zone b = 1,0 m
Moment of inertia for the cross-section I = 1,0 * 10-4 m4
Material properties
Modulus of elasticity Å = 2,1 * 1011 Pa
Modulus of subgrade reaction kz = 8,4 * 105 N/m
Loads
Concentrated vertical force F = 10 kN
Note
Variant 1.
Design model – a simple frame consisting of four bar elements of type 2.
The boundary conditions are specified by applying restraints in the X and Z degrees of freedom at the left support A and the right support C, and by imposing a restraint with finite stiffness in the Z degree of freedom at the intermediate support.
Variant 2.
Design model – a beam grillage / slab. The model consists of twelve bar elements of type 3 resting on elastic supports. The elastic supports are represented by thirteen single-node FE type 51 elements oriented along the Z axis of the global coordinate system.
The stiffness of the intermediate elastic supports is kz*b*l/12 = 347711 N/m.
The stiffness of the end elastic supports is 0,5*kz*b*l/12 = 173855 N/m.
To prevent geometric instability of the system, a restraint in the UX degree of freedom is imposed along the beam symmetry axis, and a minimum torsional stiffness of the beam is introduced GI x = 1,0 N*m2 .
Number of nodes in the design model: 13.
Output data
|
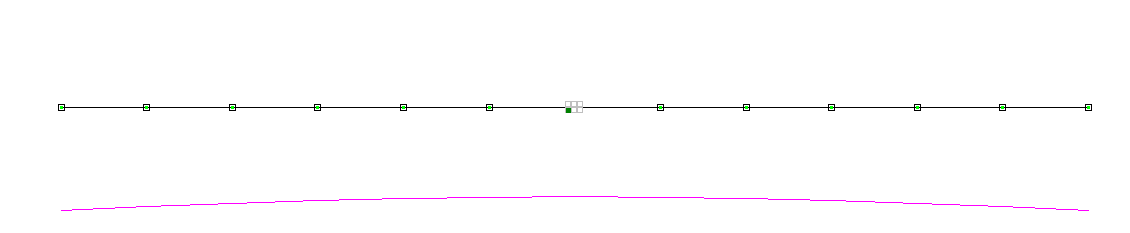
Design and deformed models. Variant 1
|
Design and deformed models. Variant 2
|
|
Vertical displacements, Z (m). Variant 1
|
Vertical displacements, Z (m). Variant 2
|
|
Rotation angle, UY (rad*1000). Variant 1
|
Rotation angle, UY (rad*1000). Variant 2
|
|
Bending moments, M (N*m). Variant 1
|
Bending moments, M (N*m). Variant 2
|
Comparison of calculation results
| Parameter | Analytical solution | LIRA-FEM | Error, % | ||
| Variant 1 | Variant 2 | Variant 1 | Variant 2 | ||
| Vertical displacement ZC , m | -6,844*10-3 | -6,843*10-3 | -6,844*10-3 | 0,01 | 0 |
| Vertical displacement ZA , m | -7,854*10-3 | -7,859 *10-3 | -7,845*10-3 | 0,06 | 0,11 |
| Rotation angle UYA , rad*1000 | -0,706 | -0,706 | -0,6945 | 0 | 1,63 |
| Bending moment MC , N*m | -5759 | -5758,8 | -5742,6 | 0 | 0,28 |
Download verification test
If you find a mistake and want to inform us about it, select the mistake, then hold down the CTRL key and click ENTER.



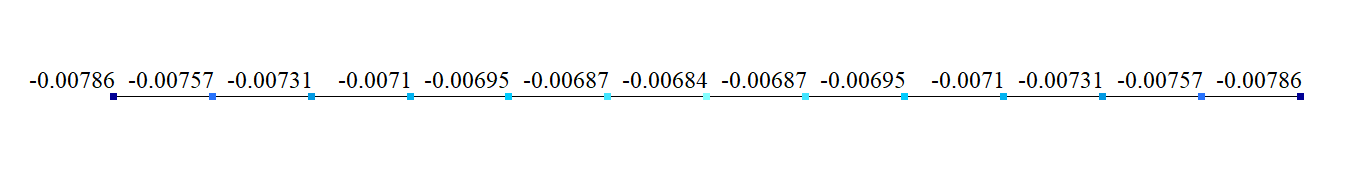
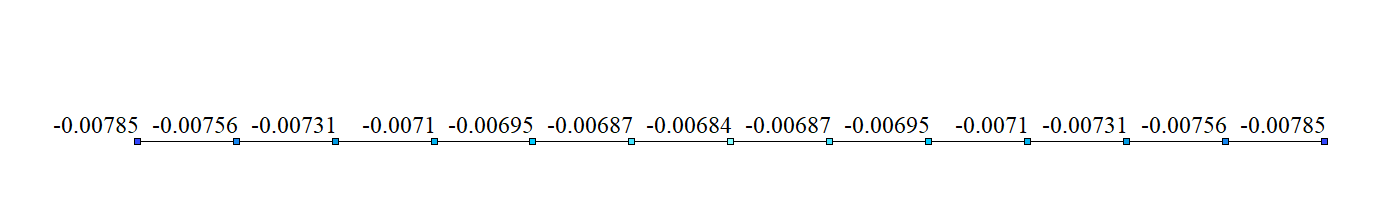




Comments