У ПК ЛІРА-САПР версії 2020 реалізовано розрахунок кам'яних та армокам'яних конструкцій по наступних нормах:
- СНиП ІІ-22-81*;
- СП 15.13330.2012;
- ДБН В.2.6-162:2010.
Розрахунок здійснюється по граничних станах першої та другої групи.
На першому етапі розрахунку всі простінки проходять перевірку по формулах для розрахунку кам'яних конструкцій. Якщо простінок не проходить перевірку щодо розрахунку кам'яних конструкцій, тоді виконується підбір арматури і здійснюється перевірка відповідного простінка по формулах для розрахунку армокам'яних конструкцій.
Даний розрахунок є універсальним для простінків будь-якої форми, тому в розрахунку не використовуються спрощені методи, запропоновані для прямокутних перерізів. Наприклад, гнучкість у цьому розрахунку, завжди залежить від радіуса інерції перерізу, а чи не від висоти перерізу. А також для більш точного розрахунку проміжних коефіцієнтів, які при спрощених методах розрахунку прямокутних перерізів можуть залежати від висоти перерізу, ми завжди приймаємо ці коефіцієнти залежними від відстані від центру ваги перерізу елемента до краю у бік ексцентриситету. Конкретні приклади вказані у формулах 2, 7, 12, 23.
1. Випадок поздовжніх зусиль стиснення (СП 15.13330.2012 і СНиП ІІ-22-81*)
1.1. Розрахунок кам'яних конструкцій
Розрахунок здійснюється по формулі:
 , (1)
, (1)
де  – коефіцієнт, що визначається по формулі:
– коефіцієнт, що визначається по формулі:
 , (2)
, (2)
де  - відстані від центру ваги перерізу елемента до його краю у бік ексцентриситету;
- відстані від центру ваги перерізу елемента до його краю у бік ексцентриситету;
 - коефіцієнт поздовжнього вигину, який визначається по формулі:
- коефіцієнт поздовжнього вигину, який визначається по формулі:
 , (3)
, (3)
де 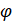 - коефіцієнт поздовжнього вигину для всього перерізу, який залежить від гнучкості простінка
- коефіцієнт поздовжнього вигину для всього перерізу, який залежить від гнучкості простінка  , яка завжди визначається по формулі:
, яка завжди визначається по формулі:
 , (4)
, (4)
де  – розрахункова довжина (висота) елементу,
– розрахункова довжина (висота) елементу,  – мінімальний радіус інерції перерізу.
– мінімальний радіус інерції перерізу.
 - коефіцієнт поздовжнього вигину для стиснутої частини перерізу, який залежить від гнучкості простінка
- коефіцієнт поздовжнього вигину для стиснутої частини перерізу, який залежить від гнучкості простінка  , яка завжди визначається по формулі:
, яка завжди визначається по формулі:
 , (5)
, (5)
де  – радіус інерції стиснутої частини перерізу, який визначається по деформаційній моделі (див. розділ 3).
– радіус інерції стиснутої частини перерізу, який визначається по деформаційній моделі (див. розділ 3).
У випадку центрального стиснення коефіцієнт поздовжнього вигину  приймається рівним:
приймається рівним:
 . (6)
. (6)
 – розрахунковий опір стиску кладки;
– розрахунковий опір стиску кладки;
 – площа стиснутої зони, у разі центрального стиску дорівнює площі всього перерізу. За наявності ексцентриситету площа стиснутої зони визначається по деформаційній моделі (див. розділ 3).
– площа стиснутої зони, у разі центрального стиску дорівнює площі всього перерізу. За наявності ексцентриситету площа стиснутої зони визначається по деформаційній моделі (див. розділ 3).
 – коефіцієнт, який визначається по формулі:
– коефіцієнт, який визначається по формулі:
 , (7)
, (7)
1.2. Розрахунок армокам'яних конструкцій
Розрахунок проводиться по формулі:
 , (8)
, (8)
Значення  ,
,  ,
,  ,
,  описані вище.
описані вище.
 – розрахунковий опір армованої кладки, який визначається по формулі:
– розрахунковий опір армованої кладки, який визначається по формулі:
 , (9)
, (9)
 – коефіцієнт, що залежить від пустотності цегли;
– коефіцієнт, що залежить від пустотності цегли;
 – розрахунковий опір арматури;
– розрахунковий опір арматури;
 – відсоток армування, який розраховується по формулі:
– відсоток армування, який розраховується по формулі:
 , (10)
, (10)
 – площа перерізу арматури;
– площа перерізу арматури;
 – розмір клітинки;
– розмір клітинки;
 – відстань між осями поперечних в'язів при сталевих обоймах або між хомутами при залізобетонних та штукатурних обоймах.
– відстань між осями поперечних в'язів при сталевих обоймах або між хомутами при залізобетонних та штукатурних обоймах.
Випадок поздовжніх зусиль стиску (ДБН В.2.6-162:2010)
1.1. Розрахунок кам'яних конструкцій
Розрахунок проводиться по формулі:
 , (11)
, (11)
де  – коефіцієнт зниження несучої здатності простінка, що визначається по формулі:
– коефіцієнт зниження несучої здатності простінка, що визначається по формулі:
 , (12)
, (12)
де  - відстані від центру ваги перерізу елемента до його краю у бік ексцентриситету;
- відстані від центру ваги перерізу елемента до його краю у бік ексцентриситету;
 – площа стиснутої зони, у разі центрального стиску дорівнює площі всього перерізу. За наявності ексцентриситету площа стиснутої зони визначається по деформаційній моделі (див. розділ 4);
– площа стиснутої зони, у разі центрального стиску дорівнює площі всього перерізу. За наявності ексцентриситету площа стиснутої зони визначається по деформаційній моделі (див. розділ 4);
 – розрахунковий опір стиску кладки.
– розрахунковий опір стиску кладки.
1.2. Розрахунок армокам'яних конструкцій
Розрахунок проводиться по формулі:
 , (13)
, (13)
Значення  описані вище.
описані вище.
 – розрахунковий опір армованої кладки, який визначається по формулі:
– розрахунковий опір армованої кладки, який визначається по формулі:
 , (14)
, (14)
 , (15)
, (15)
2. Випадки згинального моменту, поперечної сили або розтягування
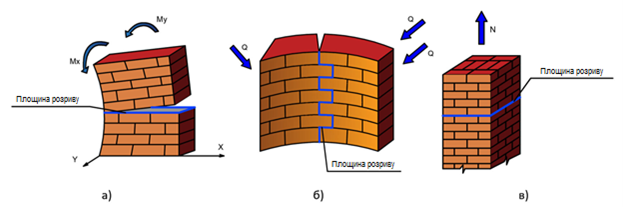
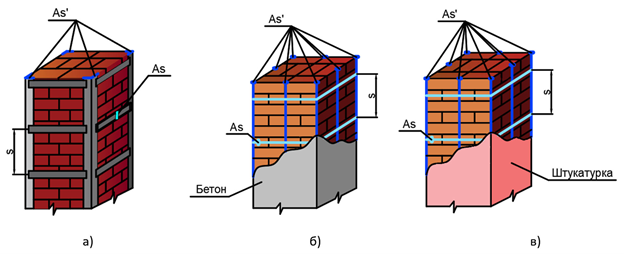
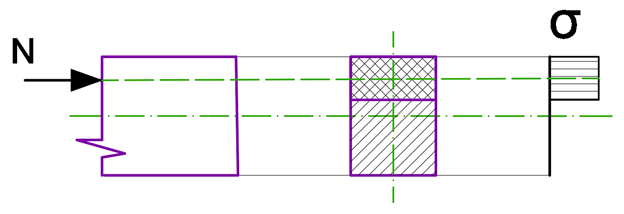
Оскільки моменти можуть бути прикладені тільки в площинах, що перпендикулярні до горизонтальних швів, розрахунок на згинальний момент проводиться по НЕперев'язаному перерізу, і розрахунковий опір кладки залежить від марки розчину (рис. 1, а).
Оскільки поперечна сила може бути прикладена в площинах, що паралельні горизонтальним швам, розрахунок на поперечну силу проводиться по Перев'язаному перерізу, і розрахунковий опір кладки залежить від марки розчину (рис. 1, б).
Оскільки розтягуюче зусилля може бути прикладене тільки в площині, що перпендикулярна горизонтальним швам, розрахунок на розтягуючу поздовжню силу проводиться по НЕперев'язаному перерізу, і розрахунковий опір кладки залежить від марки розчину (рис. 1, в).
3. Підбір параметрів для розрахунку деформаційної моделі
Площа стиснутої зони визначається по деформаційній теорії, що дозволяє врахувати нелінійну роботу цегляної кладки у перерізі. При цьому використовується кусково-лінійна залежність між напруженнями та деформаціями кладки (рис. 2).
Параметри для формування закону деформації матеріалу визначаються відповідно до розділом 6 норм СП 15.13330.2012:
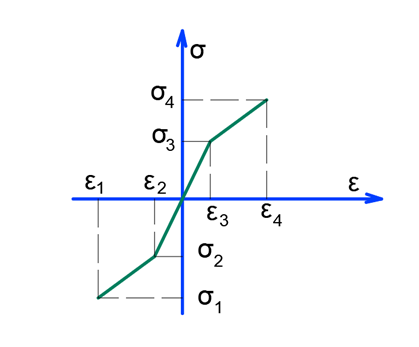
Для того, щоб знайти граничні деформації кладки  , у формулу (17), замість напружень
, у формулу (17), замість напружень  підставимо значення тимчасового опору стиску кладки, і отримаємо формулу для визначення граничних деформацій кладки
підставимо значення тимчасового опору стиску кладки, і отримаємо формулу для визначення граничних деформацій кладки  :
: 
 (18)
(18)
Таким чином, граничні деформації кладки приймаються обернено пропорційними від пружної характеристики  , яку задає користувач.
, яку задає користувач.
Оскільки формула (17) відображає нелінійну залежність між деформаціями та напруженнями, ми запишемо її у вивернутому вигляді та отримаємо формулу для знаходження граничних напружень  :
:
 (19)
(19)
4. Розрахунок по граничних станах другої групи
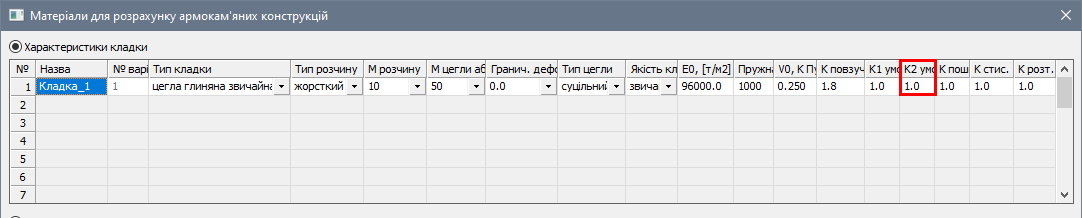
Цей розрахунок проводиться для будь-яких норм у тому випадку, якщо у діалоговому вікні «Матеріали для розрахунку армокам'яних конструкцій» коефіцієнт умов роботи К2 не дорівнює нулю, а також при наявності поздовжніх зусиль у простінку. Щоб не проводити розрахунок по граничних станах другої групи, необхідно задати коефіцієнт К2 рівним нулю (рис. 3).
Розрахунок по граничних станах другої групи провадиться по формулі:
 , (20)
, (20)
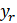 – коефіцієнт умов роботи кладки, що задається користувачем (рис. 3);
– коефіцієнт умов роботи кладки, що задається користувачем (рис. 3);
 – розрахунковий опір кладки при згині;
– розрахунковий опір кладки при згині;
 момент інерції перерізу.
момент інерції перерізу.
Результати розрахунку по другому граничному стану можна побачити у файлі звіту .txt (дивись розділ 7).
5. Посилення кам'яних конструкцій
У ПК «ЛІРА-САПР» реалізовано можливість розрахунку посилення існуючого простінка трьома методами:
- сталевою обоймою (рис.4, а);
- железобетонной обоймой (рис. 4, б);
- армированной растворной обоймой (рис. 4, в).
Розрахунок посилення провадиться відповідно до Посібника з проектування кам'яних та армокам'яних конструкцій, а саме пунктами 5.34 – 5.39.
1. Розрахунок посилення сталевою обоймою проводиться по формулі:
 ; (21)
; (21)
2. Розрахунок посилення залізобетонною обоймою проводиться по формулі:
 ; (22)
; (22)
3. Розрахунок посилення армованою розчинною обоймою проводиться по формулі
 . (23)
. (23)
Де  ,
,  – коефіцієнти, що у разі центрального стиску приймаються рівними 1, а за наявності ексцентриситету обчислюються по формулах:
– коефіцієнти, що у разі центрального стиску приймаються рівними 1, а за наявності ексцентриситету обчислюються по формулах:
 ;
;  ; (24)
; (24)
 – коефіцієнт, що описаний вище (формула 3);
– коефіцієнт, що описаний вище (формула 3);
 – коефіцієнт умов роботи кладки, який задається у полі «Характеристики кладки» діалогового вікна «Матеріали для розрахунку армокам'яних конструкцій» (рис. 5);
– коефіцієнт умов роботи кладки, який задається у полі «Характеристики кладки» діалогового вікна «Матеріали для розрахунку армокам'яних конструкцій» (рис. 5);
 – коефіцієнт, що враховує вплив тривалого впливу навантаження (формула 2);
– коефіцієнт, що враховує вплив тривалого впливу навантаження (формула 2);
 – розрахунковий опір кладки;
– розрахунковий опір кладки;
 – відсоток армування хомутами, що визначається по формулі:
– відсоток армування хомутами, що визначається по формулі:
 ; (25)
; (25)
 - площа перерізу хомутів при залізобетонних та штукатурних обоймах або поперечних планок при сталевих обоймах (рис. 4);
- площа перерізу хомутів при залізобетонних та штукатурних обоймах або поперечних планок при сталевих обоймах (рис. 4);
 ,
,  – розміри сторін підсилюваного елементу;
– розміри сторін підсилюваного елементу;
 – відстань між осями поперечних в'язів при сталевих обоймах або між хомутами при залізобетонних та штукатурних обоймах;
– відстань між осями поперечних в'язів при сталевих обоймах або між хомутами при залізобетонних та штукатурних обоймах;
 – розрахунковий опір поперечної арматури обойми;
– розрахунковий опір поперечної арматури обойми;
 – площа перерізу кладки, що підсилюється;
– площа перерізу кладки, що підсилюється;
 – розрахунковий опір куточків або поздовжньої стиснутої арматури;
– розрахунковий опір куточків або поздовжньої стиснутої арматури;
 - площа перерізу поздовжніх куточків сталевої обойми або поздовжньої арматури залізобетонної обойми (рис. 4);
- площа перерізу поздовжніх куточків сталевої обойми або поздовжньої арматури залізобетонної обойми (рис. 4);
 – коефіцієнт умов роботи бетону;
– коефіцієнт умов роботи бетону;
 – розрахунковий опір бетону обойми;
– розрахунковий опір бетону обойми;
 – площа перерізу бетону обойми, укладена між хомутами та кладкою (без урахування захисного шару);
– площа перерізу бетону обойми, укладена між хомутами та кладкою (без урахування захисного шару);
Розрахункові опори арматури, що застосовується при влаштуванні обойми, приймаються відповідно до таблиці 10 з Посібника по проектуванню кам'яних та армокам'яних конструкцій:
|
Армування |
Розрахункові опори арматури, МПа |
|
|
Сталь класу А-І |
Сталь класу А-ІІ |
|
|
Поперечна арматура |
150 |
190 |
|
Поздовжня арматура без безпосередньої передачі навантаження на обойму |
43 |
55 |
|
Те саме, при передачі навантаження на обойму з одного боку |
130 |
160 |
|
Те саме, при передачі навантаження на обойму з двох сторін |
190 |
240 |
5.1. Посилення сталевою обоймою
Для завдання розрахунку підсилення сталевою обоймою необхідно заповнити наступні поля «Характеристики зовнішнього підсилення» діалогового вікна «Матеріали для розрахунку армокам'яних конструкцій»:
У полі Стержні (клас арматури) задається клас арматури, який є однаковим для вертикальних куточків та поперечної смуги (хомута).
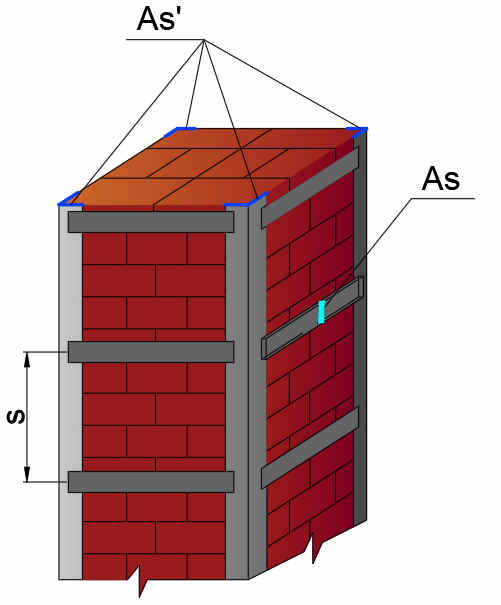
У полі Площа хомутів поперечного армування задається площа перерізу однієї планки поперечної смуги (хомута) As (рисунок 7).
У полі Площа зовнішнього посилення задається сумарне значення площ поздовжніх куточків сталевої обойми As’ (рисунок 7).
У полі Крок хомутів по висоті задається відстань між осями поперечних в'язів s (рисунок 7).
У полі КР обоймы автоматично обирається коефіцієнт умов роботи бетону, який залежить від виду Передачі навантаження з простінка на обойму.
5.2. Посилення залізобетонною обоймою
Для завдання розрахунку посилення залізобетонною обоймою потрібно заповнити наступні поля «Характеристики зовнішнього посилення» діалогового вікна «Матеріали для розрахунку армокам'яних конструкцій»:
У полі Стержні (клас арматури) задається клас арматури, який є однаковим для вертикальної та поперечної арматури.
У полі Діаметр стержнів задається діаметр поперечної арматури (хомута) Аs (рис. 9).
У полі Захисний шар вертик. арматури задається товщина бетонного шару обойми, укладена між хомутами та кладкою (без урахування захисного шару) b (рис. 9).
У полі Площа зовнішнього посилення задається сумарне значення площ поздовжньої арматури обойми As’ (рис. 9).
У полі Крок хомутів по висоті задається відстань між хомутами s (рис. 9).
У полі КР обоймы автоматично обирається коефіцієнт умов роботи бетону, який залежить від виду Передачі навантаження з простінка на обойму.
5.3. Посилення армованою розчинною обоймою
Для завдання розрахунку посилення армованою розчинною обоймою потрібно заповнити наступні поля «Характеристики зовнішнього посилення» діалогового вікна «Матеріали для розрахунку армокам'яних конструкцій»:
У полі Стержні (клас арматури) задається клас арматури, який є однаковим для вертикальної та поперечної арматури.
У полі Діаметр стержнів задається діаметр поперечної арматури (хомута) Аs (рис. 9).
У полі Крок хомутів по висоті задається відстань між хомутами s (рис. 9).
У полі КР обоймы автоматично обирається коефіцієнт умов роботи бетону, який залежить від виду Передачі навантаження з простінка на обойму.
6. Результати розрахунку
Після розрахунку, на розрахунковій схемі будуть відображені результати розрахунку простінків тільки на центральне або позацентрове стиснення. Результати розрахунку простінків на згинальний момент або на зріз можна переглянути у додатковому текстовому файлі звіту.
7. Файл звіту
Після розрахунку кам'яних конструкцій, автоматично створюється файл звіту в форматі .txt, в якому для кожного простінка записані всі проміжні розрахункові значення.
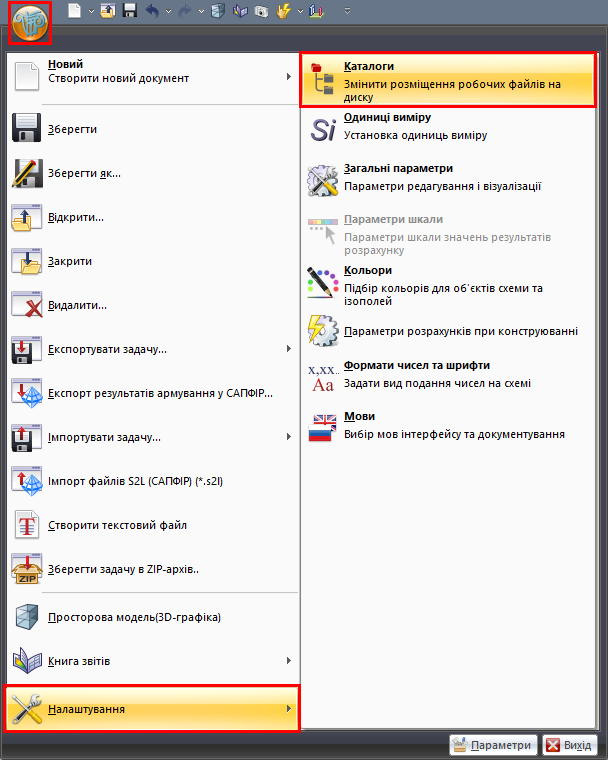
Цей файл створюється у папці Work, розташування якої можна знайти таким чином:
заходимо в Меню програми – Налаштування – Каталоги – Файли документації – Відкрити каталог за допомогою «Провідника», як показано на рисунках 11 та 12.
Як знайти потрібний простінок у текстовому файлі?
|
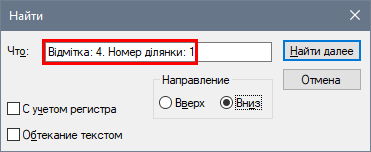
При необхідності можна отримати швидкий доступ до потрібного простінку у файлі. Для цього слід відкрити текстовий файл, натиснути
Рис. 13. Знаходження потрібного простінка
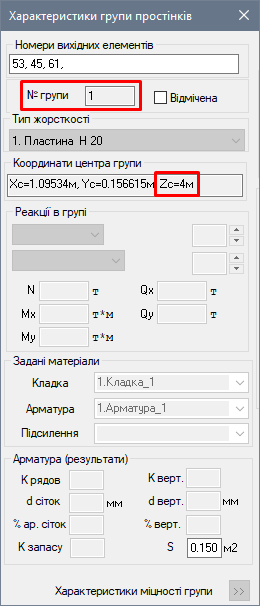
Дізнатися висоту відмітки та номер групи простінка, що цікавить Вас, можна у діалоговому вікні «Характеристики групи простінків» (рис. 14). Для того щоб відкрити це вікно, необхідно активувати функцію «ліхтарик» і вказати простінок, що цікавить Вас. |
Рис. 14. Характеристики простінків
|
8. Нелінійна деформаційна модель.
Що це і навіщо це потрібно для цегли?
Що таке нелінійна деформаційна теорія? Це метод розрахунку несучої здатності конструкції, який дозволяє врахувати нелінійну роботу матеріалу, а саме нелінійну залежність між напруженнями та деформаціями у матеріалі. Це офіційно прийнята (63.13330.2012 «Бетонні та залізобетонні конструкції. Основні положення») методика розрахунку напружень в елементі, з урахуванням фізичної нелінійності матеріалу. Іншими словами, якщо ви хочете врахувати фізичну нелінійність цегли або залізобетону, нелінійна деформаційна теорія – це допустимий спосіб це зробити.
Альтернативними методами розрахунку конструкцій є розрахунок по допустимих напруженнях, руйнівних зусиллях, граничних станах. При розрахунку по граничних зусиллях елементи можуть бути розраховані з урахуванням (рис. 16), або без урахування (рис. 17) опору бетону у розтягнутій зоні. У першому випадку зусилля у згинальному елементі визначаються по формулі:
Вираз 27 являє собою закон Гука при згині для стержня.
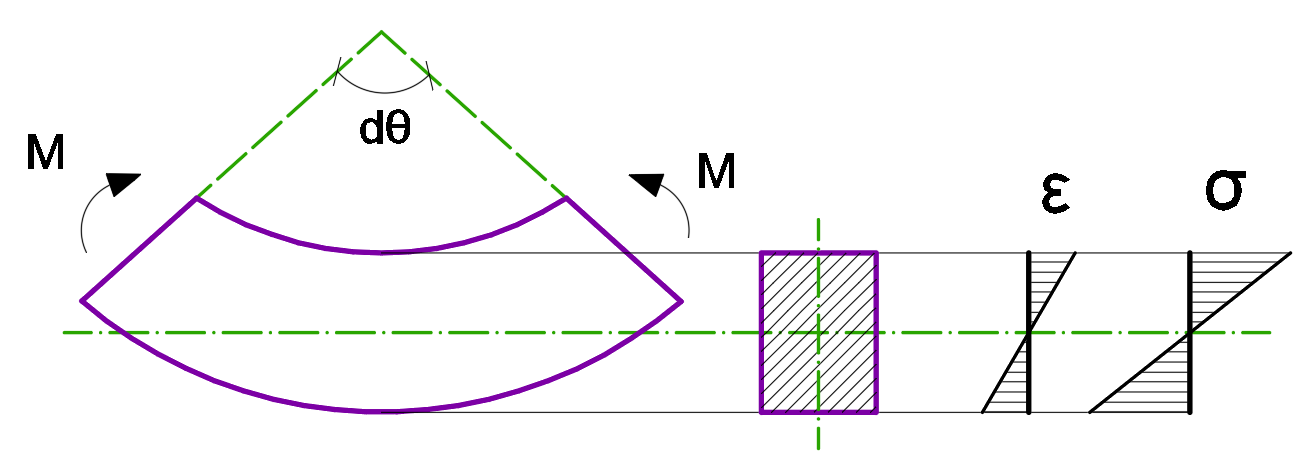
Виходячи з таких припущень, ми можемо розраховувати несучу здатність елемента за спрощеними формулами:
 ;
;
 ;
;
 ;
;
де  ,
,  ,
,  - відповідні розрахункові опори,
- відповідні розрахункові опори,  – площа перерізу,
– площа перерізу,  – момент опору перерізу,
– момент опору перерізу,  – додаткові коефіцієнти запасу.
– додаткові коефіцієнти запасу.
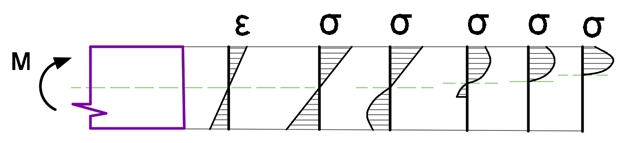
Але насправді, залежність між напруженнями та деформаціями може бути лінійною лише у разі малих напружень. Зі збільшенням навантаження, епюра напружень у перерізі стає дедалі нелінійнішою, як показано на рисунку 18.
Тому методи розрахунку, засновані на методі граничних зусиль або граничних станів, є спрощеними. Щоб правильно враховувати роботу матеріалів, потрібно враховувати нелінійну залежність між напруженнями та деформаціями. Для цього використовується нелінійна деформаційна модель.
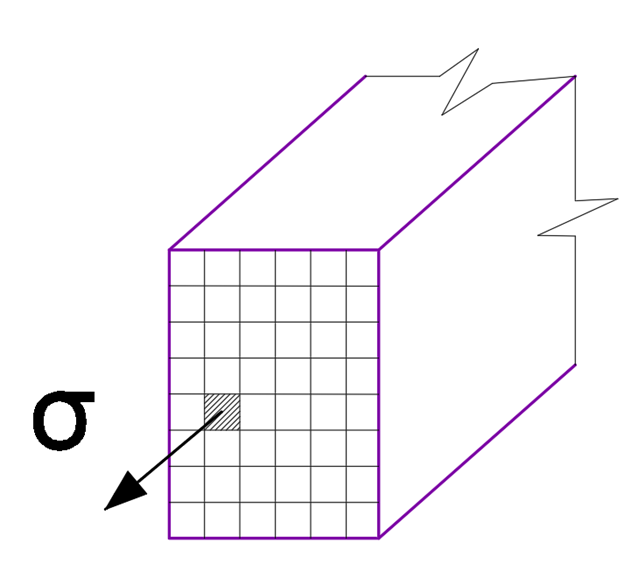
При розрахунку по деформаційній моделі, переріз розбивається на малі ділянки, далі ітераційним методом відбувається підбір (пошук) напружень на кожній ділянці (як показано на рисунку 19), які будуть задовольняти рівняння рівноваги:

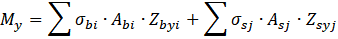

При цьому враховується нелінійна залежність між напруженнями та деформаціями, яка виражається через вибраний графік роботи матеріалу (рис. 20).
У нормах СП 15.13330.2012 запропоновано спрощену епюру напружень у перерізі, коли простінок розраховується без урахування опору кладки в розтягнутій зоні, як показано на рисунку 17.
Але згідно з пунктом 6.23, СП 15.13330.2012 для розрахунку можна використовувати нелінійну залежність між напруженнями та деформаціями. Тому, в ПК «ЛІРА-САПР» для визначення площі стиснутої зони використовується нелінійна деформаційна теорія, яка дає змогу врахувати нелінійну залежність між деформаціями та напруженнями у перерізі.
А також, завдяки тому, що при такому підході переріз розбивається на малі ділянки, відбувається більш точний розрахунок простінків неправильної форми. Наприклад, у СП сказано, що у спрощених методах розрахунку дозволяється знехтувати ділянками перерізу, які ускладнюють його форму. При використанні деформаційної теорії всі ділянки перерізу беруть участь у роботі елементу.
Помилка в тексті? Виділіть її та натисніть Ctrl + Enter, щоб повідомити нам.


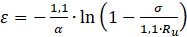











Коментарі