Глобальні, місцеві, локальні системи координат, кути чистого обертання

Моделі та їх компоненти у програмному комплексі описуються в координатних осях наступних типів: глобальних, місцевих та локальних.

Це специфічні поняття, пов'язані з особливостями формування моделі. Але попередньо вкажемо таке: названі осі не є новою невідомою системою координат. Йдеться про те, як пов'язана модель в цілому та її компоненти із застосовуваною координатною системою (прийнята декартова права система).

Глобальна система координат (g) призначена для завдання загальної геометрії системи – координат вузлів, орієнтації деяких навантажень, орієнтації місцевих (m) та локальних (l) систем координат. Глобальна система координат може бути декартовою, сферичною, циліндричною або іншою системою, яка може бути задана аналітично.

Глобальна декартова система координат позначається у програмному комплексі XYZ. Ця система прийнята за умовчанням, її піктограма виводиться в нижньому лівому куті робочого вікна.

Місцева система координат визначається для скінченного елементу і призначена для орієнтації скінченного елементу відносно глобальної системи координат, зручності побудови матриці жорсткості, завдання місцевого навантаження, визначення напружень та зусиль. Як правило, місцева система координат – декартова.

Всі скінченні елементи ПК ЛІРА-САПР, що мають більше одного вузла (одновузлові КЕ також є в програмному комплексі), орієнтовані в місцевій системі координат.

Локальна система координат (безумовно, тут можна говорити про деяку тавтологію – «місцева» і «локальна», по суті, позначають одне й те саме, проте вважатимемо, що це витрати термінології) задається для вузла і призначена для орієнтації деяких його атрибутів: вузлового навантаження, вузлових переміщень, накладених в'язів. Як правило, локальна система координат теж декартова. Реалізації різних поєднань цих систем надає багато зручностей при складанні комп'ютерних моделей.

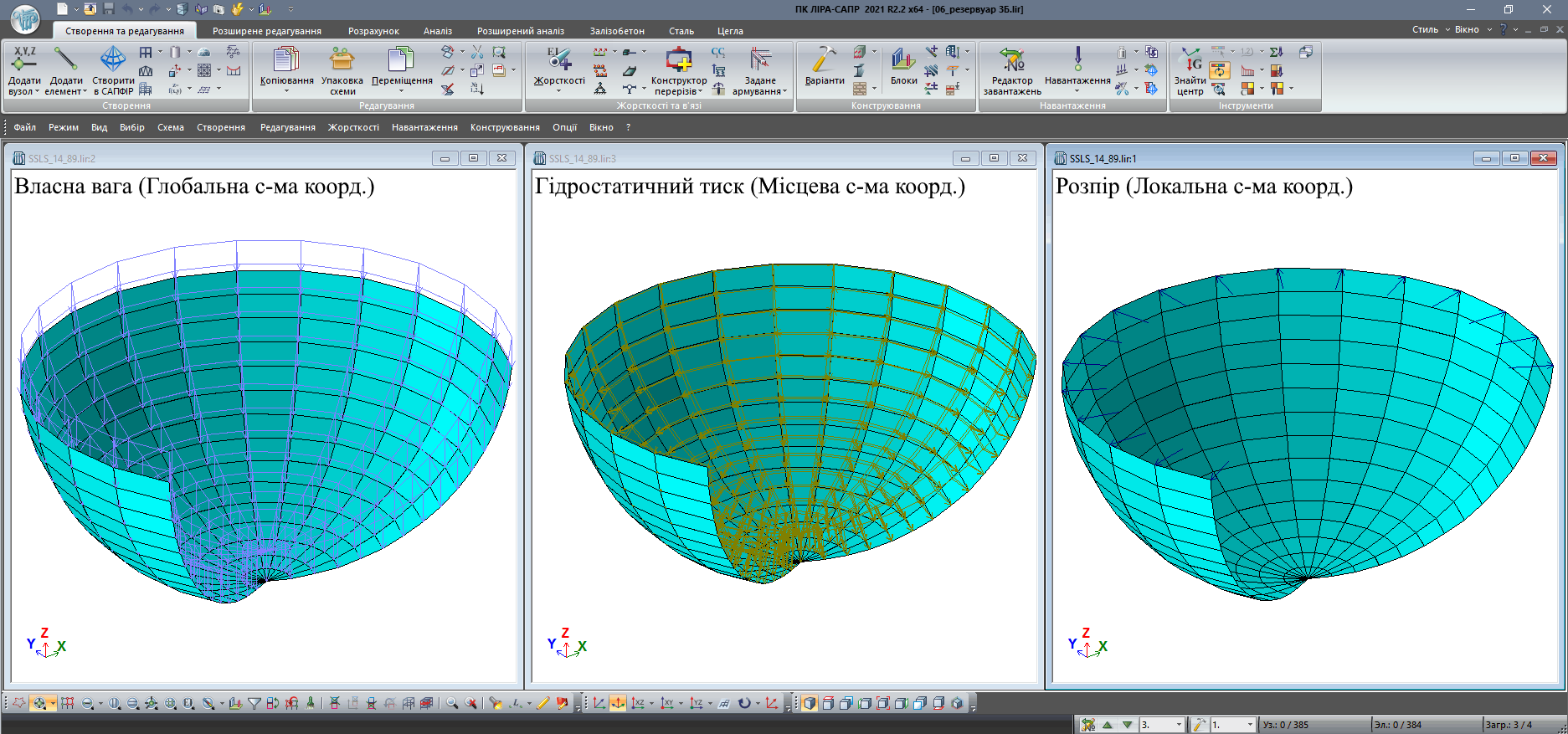
Користувач ПК ЛІРА-САПР може маніпулювати трьома типами систем координат у різноманітних поєднаннях. Так, наприклад, для гідростатичного тиску на циліндричний резервуар зручно задавати місцеве навантаження на скінченні елементи у місцевій системі координат, а при навантаженні від власної ваги зручно задавати навантаження у глобальній системі координат. Якщо необхідно задати вузлове навантаження, в'язь або організувати розрахунок на задане переміщення, напрямок яких не збігається з осями глобальної системи, то у відповідний вузол вводиться локальна система координат з потрібними напрямками.

Алгоритми побудови матриць жорсткості (МЖ) та приведення місцевого навантаження до вузлового зручно організовувати у місцевій системі координат. Це стосується як використання аналітичного виду МЖ (для кожного елемента МЖ є формула), так і при чисельному інтегруванні. Для орієнтації місцевої системи координат КЕ, які мають більше двох вузлів, достатньо мати координати трьох вузлів.

Наприклад, ось Х_m проводиться через перші два вузли (рис. 2), ось Y_m збігається з напрямком перпендикуляра до осі X_m, проходить через третій вузол, а ось Z_m утворює праву трійку.

При цьому матриця напрямних косинусів (C_mg), на основі якої здійснюється переклад атрибутів КЕ (матриця жорсткості, місцеве навантаження та ін.) з місцевої системи координат у загальну має вид:

Компоненти цієї матриці обчислюються за координатами трьох вузлів елемента (див. рис 2) у глобальній системі координат за такими формулами:

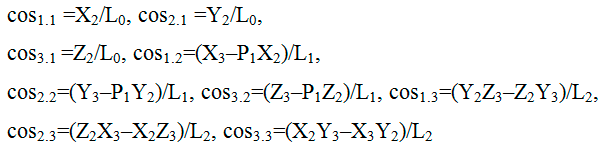
де – довжина відрізку 1–2,

– довжина перпендикуляра із вузла 3 на 1–2, ,

X₂, Y₂, Z₂, X₃, Y₃, Z₃ – координати у глобальній системі 2 та 3 вузлів відносно вузла 1, тобто X₂=X₂ – X₁ и т.д.

Для двовузлових елементів, а їх клас дуже великий (стержневі елементи), координат двох вузлів недостатньо для побудови такої матриці косинусів, для цього ще потрібна додаткова інформація, наприклад, кут чистого обертання, що визначає положення головних осей перерізу стержня відносно глобальної системи координат (рис. 3).

Як правило, ось X_m співпадає з віссю стержня (рис. 3а), а осі Y_m та Z_m є головними осями перерізу стержня. Зазвичай їхня орієнтація визначається кутом чистого обертання (усталений термін будівельної механіки стержневих систем), який є кутом між однією з головних осей перерізу (наприклад, Y_m) та віссю ОА (перетинання площини поперечного перерізу стержня, яка ортогональна осі) X_m, з площиною Х0Y глобальної системи координат).

Дуже часто напрямок Y_m задають третім вузлом, тоді побудова Cmg для стержня аналогічна елементу пластини.

Для завдання локальної системи координат необхідне завдання матриці C_lg напрямних косинусів між осями локальної та глобальної систем координат. Якщо матриця Cmg для елементів, що мають більше двох вузлів, може бути побудована на основі наявних координат вузлів, заданих у глобальній системі координат, то при заданні Cmg для стержня, а також C_lg потрібна додаткова інформація, тому програмний комплекс повинен надавати користувачеві зручний інструментарій для його задання.

При складанні канонічних рівнянь МКЕ матриці жорсткості K_m і вектори місцевого навантаження Р_m, приведеного до вузлового, необхідно переводити в глобальну систему координат, а якщо вузол має локальну систему координат, це переведення необхідно зробити з урахуванням локальної системи координат:

С_mg – матриця косинусів для переведення компонентів K_m та Р_m з місцевої до глобальної системи координат;

С_gl – матриця косинусів для переведення компонентів K_m і Р_m із глобальної в локальну систему координат.

Очевидно, що

Крім того,

Тоді для переведення вектору з місцевої системи координат у локальну використовується матриця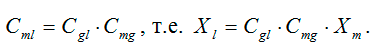

Для перетворення матриці твердості в місцевій системі координат K_m у матрицю жорсткості в локальній системі координат K_l:

Для вектору правих частин:

Для перетворення K_m на матрицю жорсткості відносно глобальної системи координат використовується формула:

, a для вектору правих частин

Переведення параметрів НДС з однієї системи координат в іншу проводиться у багатьох випадках, наприклад, обчислені у місцевій системі координат напруження (зусилля) перед побудовою ізоліній та ізополів повинні бути переведені в глобальну систему, а при побудові головних напружень мають бути вказані їхні напрямки відносно глобальної системи координат тощо.

• глобальна система координат
• локальна система координат
• місцева система координат
• матриця жорсткості